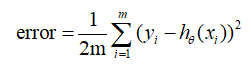1. 线性回归
什么是回归?
从大量的函数结果和自变量反推回函数表达式的过程就是回归。线性回归是利用数理统计中回归分析来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
一元线性回归:
只包括一个自变量()和一个因变量(),且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。公式:
多元线性回归:
如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。公式:
对于一元线性回归公式来说,如果给定两组x,y的值,就可以求得和的值。例如:给定两组x,y的值x=3,y=5和x=6,y=8,那么可知如下:
5=+*3 8=+*6
可以求得=2,=1。两点确定一条直线,可以确定和的值。我们可以叫做一元线性回归公式的截距,可以叫做一元线性回归公式的斜率。
假设某个医院住院人数与医院的床位个数呈线性关系,即:
住院人数 = +*医院床位数
在这里,如果想求得住院的人数,就要知道,的值,这里的,也叫权重,“医院床位数”可以理解成影响住院人数的一个维度。通过给出两组数据,就可以得到权重的值。
对于一元线性回归来说,如果现在有很多呈线性关系离散的点,假设现在需要找到一个线性回归公式来表示这些点自变量和因变量的关系,每两个点之间都能确定一条直线,如何找到一条直线来表示这些点的关系呢?
如何确定这条直线?
每一个离散的点在自变量处得到的的值记为,对应的,需要找到的这条直线在自变量处得到的的值记为,当所有的到对应的的距离差平方累加起来最小,我们就可以认为这条直线比较完美。也就是当平均误差公式:error= 最小时这条直线比较完美,其中,
代表一系列的真实离散点的y值,
代表一系列得到的直线在对应的x处的y值,一元线性回归中=。
m代表有m个离散点,前面的 是为了方便求导加上的。
表示的是一系列权重,,….
这个公式也叫做最小二乘法误差公式。error的值如果是0说明确定的这条直线穿过了所有的点,对于离散分散的一组点,error的值不可能为0。
2. 确定权重的值(确定模型)
当误差公式:
取得最小值时,能确定一条完美的直线,也就是确定一组 值与自变量的关系,拟合出来的一条直线能尽可能的通过更多的点。确定了error的最小值,也就有可能确定一组值。
如何确定error的最小值?
如果将error函数看成自变量关于error的函数,那么可以转换为:
如果将一组权重看成一列向量,表示一列维度组成的向量,就是这组向量的转置,
就是,那么现在的问题就是如何找到一组,使得error的值最小。
我们可以看出error函数的关系图像大概是一个开口向上的图像,那么当error的导数为0时,此时能得到一组的值对应的error的值最小。
通过求导的方式,理论上可以确定error的最小值,但是由于是一组数据,无法确定error最小下对应的这一组权重 。
正向的求导不能得到一组权重值,就不能确定线性回归的公式。那么可以根据数据集来穷举法反向的试,来确定线性回归的公式:
如何反向穷举求得线性回归的公式(训练线性回归模型)?
已知有线性回归关系的训练数据
已知线性回归的公式:
已知误差函数公式:
要求得在error最小下的一组权重值,以便确定线性回归的公式。我们要确定的这组就是要确定一个模型。确定模型就是确定一组参数,就是确定这组的值。
穷举之前,会有一个初始模型,一般是随机数,假设=1,=1,=1…,有了初始模型那么针对每一条训练数据都能求得一个真实值与模型评估值的平方差,也就是针对一组测试数据,能得到在这组初始模型下error误差函数的值。那么得到的error值是不是最小值?需要不断调节初始模型参数,需要在训练模型时,指定调节初始模型,,…的调节步长step(也叫学习率),迭代去求出每次调节模型后的error值,由于error的值不可能绝对的达到0(如果达到0说明训练出来的模型对应的线性回归公式完全的将所有训练数据集的点穿过),在训练模型之前指定一个最小error值,即:当迭代求出模型的error误差值小于指定的error值就停止迭代,那么当前这组值就是确定好的模型。
如果每次迭代求得模型对应的error大于指定的最小error值,要继续调节这组值,一直迭代到模型的error值小于指定的error值。
3. 梯度下降法调节参数
假设和error的函数关系中,中只有一个维度,那么这个关系其实就是和error的关系,反应图上就是一维平面关系,如果中有两个维度和,那么这个反映到图上就是个三维空间关系,以此类推。
如果中只有一个维度,如下图:
图中①,②,③,④,⑤,⑥,⑦都是图像的切线(斜率),在切点处可以求得对应的error值,如何调节模型得到一组 值可以使得到的error值更小,如图,沿着①->②->③方向调节和沿着④->⑤->⑥方向调节,可以使error值更小,这种沿着斜率绝对值减少的方向,沿着梯度的负方向每次迭代调节的方法就叫做梯度下降法。
梯度下降是迭代法的一种,可以用于求解最小二乘问题,在求解error函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的error函数和模型参数值。
每次按照步长(学习率)来调节值,迭代求出error的最小值,这里的error不可能有一个固定的最小值,只会向着最小值的方向收敛。
判断模型error误差值收敛,也就是停止迭代的两种方式:
- 指定一个error值,当迭代处理过程中得到的error值小于指定的值时,停止迭代。
- 设置迭代次数,当迭代次数达到设置的次数时,停止迭代。
迭代周期:从调整参数开始到计算出error值判断是否大于用户指定的error是一个迭代周期。
当步长比较小时,迭代次数多,训练模型的时间比较长,当步长比较大时,有可能迭代的次数也比较多,训练模型的时间也会相对比较长,需要找到一个合适的步长。