Keras - Batch normalization 理论与实践

一.引言

根据论文《Batch Normalization: Accelerating Deep Network Training b y Reducing Internal Covariate Shift》所述，神经网络训练过程中，每层输入的分布随着前一层参数的变化进行训练，这就导致了上层网络需要不断调整参数适应不同分布的输入数据，这不仅降低了训练的速率，也使得很难训练得到具有饱和非线性的模型。我们称之为 Internal Covariate Shift，翻译下来是内部协变量位移，其实就是指隐层数据分布随网络参数变化而变化的情况。为此我们引入了Batch Normalization 即规范化层输入来解决问题，这允许我们使用更高的学习率同时不必在参数初始化时太过谨慎，它还可以作为正则化在某些情况下减少对 Dropout 的需求。

二.Batch normalization 理论

顾名思义，Batch normalization (之后都用BN代替) 是对一个 batch 的数据作归一化，其可以看作是一个层，一般添加在全连接层后。按照论文的描述，其操作步骤如下:

CSDN-BITDDD

其中针对每一个 mini-batch 的数据(共m条样本)，分别求其均值与方差并标准化 xi，这里方差部分用到了  (epsilon) 是一个小常数，防止分母为0的情况发生。注意最后的输出并不是标准化后的 xi，而是经过了缩放和平移的

                                                   

这里 γ(gamma) 和 β(beta) 是需要学习的参数。需要注意的是 BN 层在训练和预测时的逻辑是不同的，下面简单区分一下。

1.BN层基本参数

先说下 BN 层的基本参数:

(1) γ(gamma) : 需要学习的缩放因子，即上图的 scale，初始化为1

(2) β(beta) : 需要学习的偏移因子，即上图的 shift，初始化为0

(3) momentum : 滑动平均的动量因子

(4) moving_mean : 滑动均值，不需要学习的参数，根据每轮训练更新，根据每一个batch的均值的更新:

          

(5) moving_var : 滑动方差，不需要学习的参数，根据每轮训练更新，根据每一个batch的方差的更新:

           

2.Batch normalization 训练

训练期间，均值和方差的计算来自当前的 mini-batch，scala 和 shift 值是模型学习得到的(Tips: BN层的 trainable 参数默认是 False，所以训练期间一定要记得设置为 True)，全局的滑动均值与滑动方差则是根据 momentum 在训练过程中更新，即训练时BN层返回:

           

3.Batch normalization 预测

预测期间用到了训练期间一直更新的全局的滑动平均与滑动方差值，训练与预测的主要不同就是均值与方差的获取方式，常量   (epsilon) 保持不变: 

            

三.Batch normalization 实践

1.试验设置

实验数据采用 mnist 手写识别数据，手写数字识别中有一个归一化的操作是:

    train_images = train_images.astype('float32') / 255

这是因为图像像素是0-255的数值，通过 / 255 将图像的像素归一化到 0-1 的数值，方便模型学习，下面做4组对照试验:

试验设置

A	归一化数据  (0-1)	无 Batch normalization
B	归一化数据  (0-1)	有 Batch normalization
C	未归一化数据  (0-255)	无 Batch normalization
D	未归一化数据  (0-255)	有 Batch normalization

2.数据获取

get_train_test_data 分别获取归一化和未归一化的训练测试数据以及对应 label。

def get_train_test_data():
    (train_images, train_labels), (test_images, test_labels) = mnist.load_data()

    train_images = train_images.reshape((60000, 28 * 28))
    ori_train_images = train_images
    train_images = train_images.astype('float32') / 255

    test_images = test_images.reshape((10000, 28 * 28))
    ori_test_images = test_images
    test_images = test_images.astype('float32') / 255

    train_labels = to_categorical(train_labels)
    test_labels = to_categorical(test_labels)
    print("原始训练集维度: ", ori_train_images.shape, " 训练集维度: ", train_images.shape, " 训练标签维度: ", train_labels.shape)
    print("原始测试集维度: ", ori_test_images.shape, " 测试集维度: ", test_images.shape, " 测试标签维度: ", test_labels.shape)
    return ori_train_images, train_images, train_labels, ori_test_images, test_images, test_labels

    (ori_train_images, train_images, train_labels, ori_test_images, test_images, test_labels) = get_train_test_data()

3.模型构建

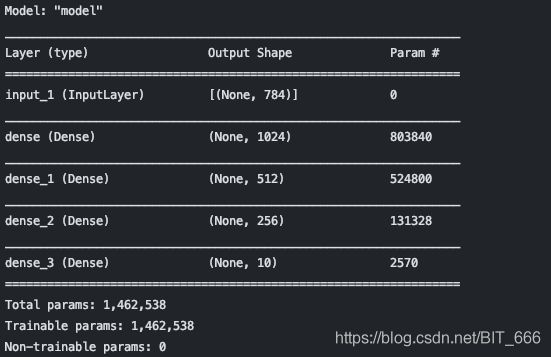
这里采用3个 Dense 层构建 Baseline 模型，隐层参数分别设置为1024，512，256 

(1) BaseLine Without Batch normalization

经典的 Dense 层连接

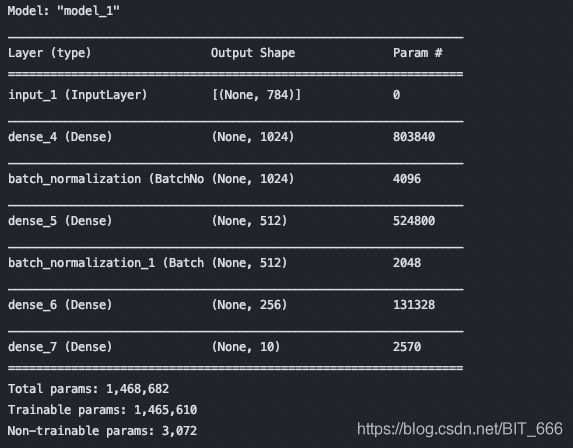
(2) Baseline With Batch normalization

在三个 Dense 层之间增加了两个 BN 层，其余一致，注意 BN 的 trainable 设置为 True。

BatchNormalization(trainable=True)

4.模型训练结果

Tips ：每次实验结果可能不一致，也可以多次试验取平均

进行两两对照实验比对:

A-B -> 归一化数据下是否包含BN影响不大，但是添加了BN层的模型各项指标均稍有提升

C-D -> 未归一化数据情况下包含 BN 影响较大，相差1个点，Loss 值相比归一化的数据也更大

A-C -> 相同模型，数据是否归一化对模型效果有较大影响，相差约1个点

B-D -> 相同模型，数据是否归一化在包含 BN 层下影响较小，acc 和 loss 都小幅下降

实验	数据样式	是否包含BN	Test Acc	Test Loss
A	归一化数据  (0-1)	无 Batch normalization	0.9789	0.1826
B	归一化数据  (0-1)	有 Batch normalization	0.9804	0.1260
C	未归一化数据  (0-255)	无 Batch normalization	0.9696	0.6121
D	未归一化数据  (0-255)	有 Batch normalization	0.9797	0.1433

5.BN 可视化

下面我们取一条测试样本，比较一下 C,D 实验三个隐层的激活输出图，感受一下 BN 层的作用 :

CSDN-BITDDD

不包含 BN 层的数据由于数据分布比较分散，随着激活函数的激活，前向传播的信息越来越少，这也就是为什么随着层数增加常常出现梯度消失的情况。

CSDN-BITDDD

包含 BN 层归一化数据，使得更多的权重得到训练，更多的信息向后面的层传播，可以让原始信息更好的传递下去。

四.总结

简单来说，由于数据分布的不一致性会导致模型训练过程中存在:

(1) 模型参数不断调整适应新数据 -> 降低训练效率

(2) 训练效率降低，模型训练不易收敛 -> 梯度消失 

采用 BN 可以有效传递原始数据信息，避免梯度消失的情况，提升模型学习效果。