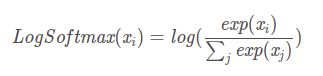softmax()和log_softmax()、CrossEntropyLoss()和NLLLoss()对比分析

目录

一、softmax()和log_softmax()

二、CrossEntropyLoss()和NLLLoss()

---

softmax()和log_softmax()、CrossEntropyLoss()和NLLLoss()都是我们深度学习中常用的函数或者常见的概念，平时大家都用习惯了，我也用习惯了，并没有对它们做一个整体性的比较和分析。下文对上面提到的4个概念或者函数做一个对比和分析，加深对一些基础知识的理解吧。

一、softmax()和log_softmax()

softmax

softmax函数的计算方式：对输入的每个元素值，求以自然常数e为底的指数，然后除以它们整体的和。具体的公式如下：

log_softmax

它的含义非常简单和明确，就是对softmax求出来的值在进行一次求对数。计算公式如下：

可以看到softmax可以进行值域压缩——[0,1]之间，并且使得它们的值为1，这里的含义就有点概率的意思了；log_softmax就把经过softmax压缩过的值，扩充到[-inf,0]之间。

这里再多说一点点就是在神经网络多分类任务中为何要使用softmax函数来进行归一化。很直观的解释就是它能平衡概率分布，避免其他归一化方法出现概率为0的问题。

具体的表现形式上的差异已经出来了，那么为什么有了softmax后还要设计log_softmax函数呢？就应用场景而言，分类任务的时候，需要计算损失，而这整套流程下来，却是包含了softmax()函数归一化的过程同时还有对归一化后的值取对数的操作；另外softmax必然具有一定的缺陷和问题，为了克服这些缺陷和问题，才设计出log_softmax。

softmax的数值计算问题

在使用softmax函数的时候，大概率下不会出现数值计算问题，只有当输入x的绝对值是一个很大的值的时候才会出现数值计算问题。当x是一个很大的正数，softmax就会出现上溢出的问题——应为程序在计算的过程中第一步是计算分子上的exp(x),当x是极大的正值，程序的数据类型float或者double表示不出来，就会报错；当x是一个极小的负值，exp(x)趋近于0，在程序中就会被记为0，当所有的X都是极小的负值，整个分母就会被记为0，那么运算过程中就会出现错误——下溢出。

log_softmax

为了解决上述softmax在数值计算的问题，就设计了log_softmax。当然从公式直接看：log_softmax = xi - log([exp(xi)])。这里仍然没有解决上溢出和下溢出的问题。学者们很聪明的设计了一种很巧的办法：

通过设计：M为输入Xi中的最大值。这样log_softmax就转化为了图片中的公式，蓝色框框中的。有可能出现溢出的问题就在红色框框的那一坨公式里。简单分析一下，当xi为正数的时候，xi-M都不会出现大于0的数字，所以上溢出问题就解决了；当xi-M都是很大的负值，但是一定有一个xi-M==0，这样就保证红色框框那一坨公式等价于log(x),其中x>1并且不是一个很大的数字(如果x接近0，那么log(x)就是接近负无穷大，就会出了溢出问题)，这样就解决了下溢出的问题。

当然这样操作起来，就会在计算过程中log_softmax和log(softmax)有一定的差异。

softmax和log_softmax验证

直接模拟一个分类器，上代码：

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
#设置随机种子保证复现性
torch.manual_seed(1)
if __name__ == '__main__':
    classifier = nn.Linear(4,2)
    embeddings = torch.randn((5,4))
    output = classifier(embeddings)

    softmax = F.softmax(output,dim=1)
    print('softmax')
    print(softmax)
    print('*'*100)
    #验证概率为1
    softmax_sum = torch.einsum('ij -> i',[softmax])
    print('softmax_sum验证概率为1')
    print(softmax_sum)
    print('*'*100)
    log_softmax = torch.log(softmax)
    print('log(softmax)')
    print(log_softmax)
    print('*'*100)
    logsoftmax = F.log_softmax(output,dim=1)
    print('logsoftmax')
    print(logsoftmax)
    print('*'*100)
    #验证log(softmax)和logsoftmax是否相等
    print('验证log(softmax)和logsoftmax是否相等')
    print(torch.equal(log_softmax,logsoftmax))
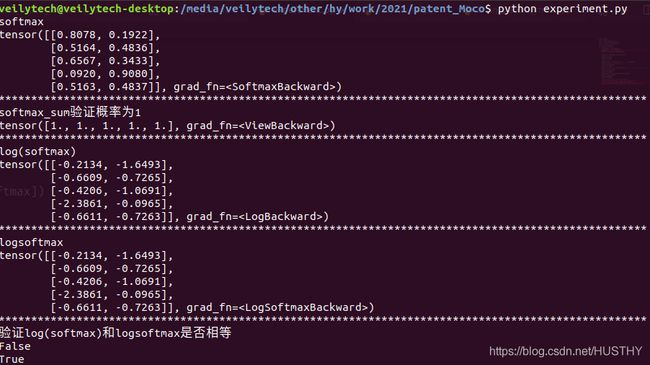
    print(torch.equal(log_softmax.half(),logsoftmax.half()))

结果如下：

可以得出：

1、softmax确实进行了归一化

2、log(softmax)和log_softmax()在pytorch实现下，并不完全相等的。(代码中float32精度下就不想等，而float16——也就是half()下是相等的)

log_softmax的优势就是计算过程更加平稳，不会出现溢出问题，同时相比如先softmax然后在log两次操作更加的方便和快速。

二、CrossEntropyLoss()和NLLLoss()

这里讨论都是基于pytorch框架下实现的损失函数。

CrossEntropyLoss()

首先看看CrossEntropyLoss()函数的计算公式：

从pytorch官网API文档中可以看到CrossEntropyLoss()就是对网络的输出先做了softmax操作，然后再取对数。那么交叉熵损失到底度量的是一个什么东西？

信息量：它是用来衡量一个事件的不确定性的。一个事件发生的概率越大，不确定性越小，则它所携带的信息量就越小；事件发生的概率越小，不确定性就越大，信息量就越大。则信息量定义为：I(x) = -log[p(x)]。

熵：它是用来衡量一个系统的混乱程度的，代表一个系统中信息量的总和；信息量总和越大，表明这个系统不确定性就越大。

交叉熵：它主要刻画的是实际输出（概率）与期望输出（概率）的差异，也就是交叉熵的值越小，两个概率分布就越接近。

NLLLoss

NLLLoss的具体描述如下：

negative log likelihood loss——可以看到就是对网络输出取了一个负号——负对数似然损失——这里并没有进行取对数，具体怎么形容它的含义没想到合适的描述——刻画的是输出与实际的相异性？

这两个函数一般都是用在分类任务中的，CrossEntropyLoss()等价于log_softmax()+NLLLoss()——pytorch框架实现都是一模一样的。另外单独使用NLLLoss损失函数的任务我还没有接触到过，后续有机会接触到了再来更新。

下面对CrossEntropyLoss()和log_softmax()+NLLLoss()进行简单的验证，上代码：

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
#设置随机种子保证复现性
torch.manual_seed(1)
if __name__ == '__main__':
    #把batch内的每个样本的loss都分别记录下来
    criterion = nn.CrossEntropyLoss(reduction='none') 
    criterion1 = nn.NLLLoss(reduction='none')
    criterion_mean = nn.CrossEntropyLoss() 

    classifier = nn.Linear(4,2)
    embeddings = torch.randn((2,4))
    output = classifier(embeddings)
    label = torch.tensor([1,0],dtype=torch.long)

    entropy_loss = criterion(output,label)
    print('entropy_loss',entropy_loss)

    print('*'*100)
    log_softmax = F.log_softmax(output,dim=1) 
    print('log_softmax',log_softmax)

    nll_loss = criterion1(log_softmax,label)
    print('nll_loss',nll_loss)
    print('*'*100)
    entropy_loss_mean = criterion_mean(output,label)
    print('entropy_loss_mean',entropy_loss_mean)
    print('*'*100)
    print('entropy_loss mena',entropy_loss.mean())

上面的代码比较简单，分别进行了CrossEntropyLoss和CrossEntropyLoss——batch平均以及NLLLoss损失的计算，结果如下图

可以看到entropy_loss的值和nll_loss的值是一样的;同时最后的均值验证显示，reduction系数默认的mean计算的结果确实是正确的——(0.9203+1.1605)/2 =1.0404;最后NLLlos的结果显示，就是在log_softmax得到的结果对对应的label一样的index处的值取负号。

 

以上就是这次博文的全部内容了，softmax确实是一个很好的归一化方法，能够把一组值归一化为一组概率分布；log_softmax则解决了softmax出现的数值溢出问题；在计算神经网络的损失的时候，log_softmax可以全部替换掉softmax,尤其是在CrossEntropyLoss和NLLLoss进行分类任务的时候；还有一个重要的结论就是CrossEntropyLoss()等价于F.log_softmax()+NLLLoss()。

 

 

log_softmax与softmax的区别在哪里？

Pytorch常用的交叉熵损失函数CrossEntropyLoss()详解