Batch Normalization详解
这几天重新看了BN,完成了翻译,也仔细的对里面一些自己感到疑惑的点,进行了查阅和思考,其中有一些个人见解,欢迎大家来讨论。
本文分两个部分,第一部分对BN进行一些基本讲解,第二部分讲其他的一些Normalization方法。
Batch Normalization
1 问题
首先我们要明白BN想要解决的问题是什么,参考原文我们发现,随着网络越来越深,训练深度网络变得很困难,收敛速度很慢。
1.1 原因
原文告诉我们是因为 Internal covariate shift (ICS)现象以及梯度弥散等问题。ICS,简言之就是网络中间层输入数据分布的不断变化,这样就导致网络后面层被迫去追随这种变化。
1.2 原来的方法
没有BN之前,网络也是要训练的,那么怎么保证收敛呢,原文提到,一是使用较小的学习率,二是对参数初始化进行精心设计。
1.3 BN的好处
自然有了BN之后,就能加快深度网络的训练,加快收敛。那BN的优势就在于。一,解决了(或者说减弱了)ICS现象;二,解决了梯度弥散;三,减小了对于学习率和初始化的依赖;四,引入了一定的泛化效果。
2 BN的思路
现在我们从问题出发,也就是我们知道现在网络收敛慢的原因了——ICS,那么我们如何来进行突破呢?从ICS的字面上,我们知道是因为中间层的输入数据分布的不断变化导致的。那么自然就想到固定每一层的输入数据分布,岂不是就可以了。那么问题又来了,如何固定呢,应该选择怎样的分布来进行固定呢?
2.1 数据白化(标准化)
做深度学习或机器学习的人们都知道,在训练之前,我们的数据都是要进行预处理的。要么做数据白化(使数据不同维度去相关,使数据每个维度的方差为1),让数据近似满足独立同分布的条件,或者退而求其次,做数据标准化(减去均值,除以方差),让数据满足近似的同分布。然后这样做了,就可以加快模型的收敛。
2.1.1 原因
那么为什么做了这样的数据预处理就可以加快收敛呢?请参考博主很早的博客feature scaling以及Efficient BackProp
2.2 子网络
这里我们引入子网络的概念,正常一个N层的网络,我们剥离开第1层,那么剩下的N-1层可以看成是一个新网络,它就是原来网络的一个子网络,那同理,剥离掉第1,2层,剩下的N-2层又是一个新的子网络。
结合2.1,我们知道了对输入数据做白化是能加快收敛的,那么对于子网络的输入数据做白化按理来说也是可以加快收敛的,以此类推。
我们结合2.1和2.2,是不是就回答了我们刚才的问题,那么BN的思路就是对每一层进行数据白化。
3 BN里面的简化处理
我们已经知道我们要怎么做了,可是真正做的时候遇到一些阻碍,需要进行简化处理,原文提到了两种简化处理。
3.1 标准化取代白化
做数据白化是很繁琐且计算量巨大的,因为涉及到协方差矩阵的运算,要求取所有特征之间的协方差,同时在反传的时候还要求取相应变换,这会随着特征的增多而指数性的增长,因此,我们退而求其次,进行简单的标准化处理。就像计算机视觉中,对于输入图像,我们往往进行简单的标准化处理,而非白化处理。
3.2 使用mini-batch统计信息来近似全局分布
既然要进行标准化处理,就涉及到对于每个特征的均值和方差的求取,原则上我们是希望使用全局的训练数据来统计均值和方差的,但是使用SGD的话,或者说mini-batch SGD的话,我们无法得到全局的信息(我们虽然有所有的训练数据,但是我们也只能求到输入层的均值和方差,我们无法得到中间层的均值和方差,因为它们是在随时变化的)。所以我们使用mini-batch来生成每个特征的均值和方差的估计。
4 BN公式
5 疑问
我第一次看到这个公式的时候,讲道理是一头雾水,前面顺下来都讲的通,你让我标准化,那我就给你标准化,然后你又告诉我要进行平移缩放,wat?仿佛在玩我的样子,这里自然就有海量疑问。
5.1 为什么要进行再次的缩放和平移?
对于这个地方,原文真的是一笔带过,虽然加入了斜体,但真真是轻描淡写,the transformation inserted in the network can represent the identity transform。也就是现在我们已经完成了标准化了,每一层的输入都被我们强行调整成了近似0均值,1方差。那么直观上来讲,就是我学了半天,你给我标准化了,我再学,你再标准化,我岂不是白学了。所以为了解决这个问题,需要进行缩放和平移,来以网络自己学习的方式来复原该层所学习到的东西,它可能是完全复原,也可能变成别的分布,这样就是所谓的恢复了模型的容量(capacity),恢复了网络的表达能力。
5.2 两次变换是否有用,是否会相互抵消,是否真的有效?
首先需要肯定的是,这两次变换肯定是有效的,毕竟BN已经被反复验证是work了的,个人觉得,这样看似矛盾的来去变换其本质是在进行参数更新的解耦,让各自层的参数尽量各自的学习,减少层之间的影响。这里从反传梯度的角度来看一下。
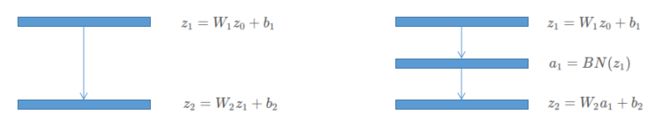
左图为我原始网络的其中两层,右图为在其间加入BN层,这里我将激活函数省略了。
ICS现象告诉我们,后面层会因为前面层的输出的不断变化而迫使自己不断的去学习这个新的分布,所以我们主要看 W 2 W_2 W2的更新情况。
左图原始的参数更新:
∂ ℓ ∂ W 2 = ∂ ℓ ∂ z 2 ∂ z 2 ∂ W 2 = ∂ ℓ ∂ z 2 z 1 ∝ z 1 \frac{\partial \ell}{\partial W_2}=\frac{\partial \ell}{\partial z_2}\frac{\partial z_2}{\partial W_2}=\frac{\partial \ell}{\partial z_2}z_1\propto z_1 ∂W2∂ℓ=∂z2∂ℓ∂W2∂z2=∂z2∂ℓz1∝z1
右图:
∂ ℓ ∂ W 2 = ∂ ℓ ∂ z 2 ∂ z 2 ∂ W 2 = ∂ ℓ ∂ z 2 a 1 ∝ a 1 a 1 = γ z ^ 1 + β ∂ ℓ ∂ γ = ∂ ℓ ∂ z 2 ∂ z 2 ∂ a 1 ∂ a 1 ∂ γ = ∂ ℓ ∂ z 2 W 2 z ^ 1 ∝ W 2 z ^ 1 \frac{\partial \ell}{\partial W_2}=\frac{\partial \ell}{\partial z_2}\frac{\partial z_2}{\partial W_2}=\frac{\partial \ell}{\partial z_2}a_1\propto a_1 \\ a_1 = \gamma \widehat z_1+\beta \\ \frac{\partial \ell}{\partial \gamma}=\frac{\partial \ell}{\partial z_2}\frac{\partial z_2}{\partial a_1} \frac{\partial a_1}{\partial \gamma}=\frac{\partial \ell}{\partial z_2}W_2 \widehat z_1\propto W_2 \widehat z_1 ∂W2∂ℓ=∂z2∂ℓ∂W2∂z2=∂z2∂ℓa1∝a1a1=γz 1+β∂γ∂ℓ=∂z2∂ℓ∂a1∂z2∂γ∂a1=∂z2∂ℓW2z 1∝W2z 1
那么从反传的上下对比的话,我们可以明显的看出,新参数的学习形态与原参数完全不同了,不再与上一层的输出有着直接的关系,甚至说关系很小了。
也就是虽然再一次的平移变换,可能会完全复原以前的数据分布,但是在后续的梯度反传,参数更新的的时候,它们将朝着不同的方向更新了。也就所谓的我不会再根据你变化来变化了,我现在就自己在学习,在学习自己的分布。
那么我们再换一个角度来想,
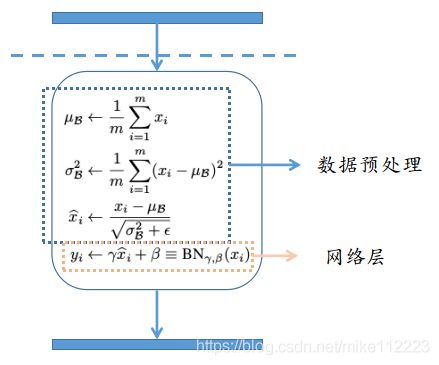
对于每个BN层,我们将其与前面层分开,我们看该BN层与其后面网络层所组成的子网络,BN的前三步就是数据预处理的部分,BN的第四步只是单纯添加了一层网络层。那么其实就很像是在单独的训练一个网络,这样也同样印证了这个解耦操作,减弱了ICS。
6 Inference
前面的部分已经基本理清楚了BN的操作以及对一些疑问的解答,那么接下来我们考虑infer的时候是如何使用BN的,因为训练的时候用了BN,自然测试的时候也要使用。但是测试的时候,就会遇到问题,这个时候,我们没有mini-batch这个概念了,测试样例可能是一个个过来的,所以无法通过训练时候mini-batch的方法求得均值和方差。
这个时候网络已经训练完毕,理论上是希望使用全部训练数据来得到一个均值和方差来用于测试。这里依然是考虑到训练样本总数可能太过庞大,还有就是在训练的时候也希望能够跟踪我们模型的准确率,所以考虑在训练的时候使用滑动平均的方式来对均值和方差的无偏估计进行一个跟踪和保存,然后最后infer的时候,就使用这个保存的值。
7 BN的好处
1.3节我们提到了BN的优势和好处,一共有4点,前面其实我们只讲到了一点,减弱了ICS现象。本节,我们讲剩下的三点。
7.1 梯度弥散
原文讲到的是,BN能够使得带饱和激活的网络也能够收敛,我们知道sigmoid两侧是梯度饱和区,中间是线性区域,那标准化之后,自然特征的都移动到了线性区域,就没有了梯度弥散的问题,可以加快收敛。
7.2 减小对学习率和初始化的依赖
在没有BN的时候,我们要训练深度网络是无法使用很大的学习率的,这是因为太高的学习率会导致梯度的爆炸或者弥散,使得模型无法训练,使用了BN之后,防止参数的小的变化被放大,增加了训练对于参数尺度变化的韧性。下式就反映了这一点
∂ BN ( ( a W ) u ) ∂ u = ∂ BN ( W u ) ∂ u ∂ BN ( ( a W ) u ) ∂ ( a W ) = 1 a ⋅ ∂ BN ( W u ) ∂ W \begin{aligned} \frac{\partial \text{BN}((a W)\text u)}{\partial \text u}=\frac{\partial \text{BN}(W\text u)}{\partial \text u} \\ \frac{\partial \text{BN}((a W)\text u)}{\partial (aW)}=\frac{1}{a} \cdot \frac{\partial\text{BN}(W\text u)}{\partial W} \end{aligned} ∂u∂BN((aW)u)=∂u∂BN(Wu)∂(aW)∂BN((aW)u)=a1⋅∂W∂BN(Wu)
就算使用大的学习率,让参数的变化幅度增大,但是在梯度反穿的时候,这种类似缩放的尺度变化会被BN吃掉。甚至对于大参数的梯度还有抑制的作用,也就是越大的权重梯度越小,这就保证了所有参数的稳定训练。其实这里也同时说明了BN对于梯度弥散和梯度爆炸的抑制。
7.3 泛化效果
训练时,每个mini-batch的平移缩放过程使用的均值和方差都是基于该mini-batch来计算的,就算是同样的样本, 在不同的mini-batch里,它的输出也是不一样的,这里就引入了噪声,自然引入了噪声就带入了泛化的效果。
8 CNN里的BN
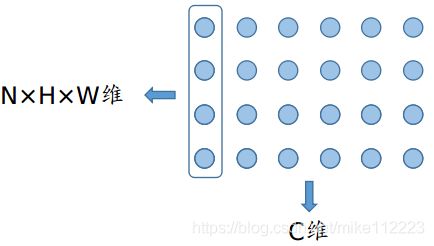
对于d维数据,也就是d维向量,我们知道均值和方差是在每个特征维度上用mini-batch来进行统计的,如下图带框的部分,也就是特征维度的标准化,对不同样本的同一个特征进行平移缩放。

那对于CNN,我们要如何来做BN呢?这时我们的特征从 ( m , d ) (m,d) (m,d)变成了 ( N , C , H , W ) (N,C,H,W) (N,C,H,W),如果直接照搬的话,就如下图,等同于将一个batch里的每张图片的对应通道的对应像素来进行标准化。但是很明显这种方法是不对的,因为每张图片的对应通道的对应像素并不代表一种特征,它们只是单纯的位于图像的同一个位置。

那么具体应该怎么做呢,按原文来说,通道才是我们的特征维度,所以我们一个batch的大小从 N N N 变成了 N × H × W N \times H \times W N×H×W。这样做其实才是符合我们对于卷积网络的假设的,因为图像具有局部相关性,所以我们使用卷积的方式来提取一个patch的局部特征,而每个通道的特征图是使用同一个卷积核卷积出来的,自然就是同一种特征了(比如都是提取横向的edge),那这样的话,就可以对其进行标准化。
其他 Normalization
接下来我们讲解一下其他的Normalization。先放出这张图,能够很大程度上,帮助理解接下来的几种不同的normalization。
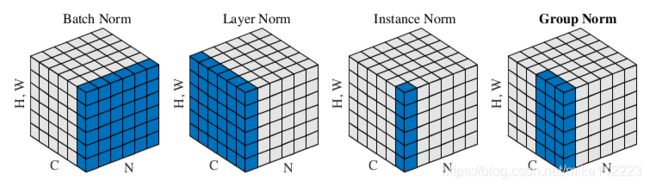
Layer Normalization
BN是需要对输入数据求取滑动平均的。对于拥有固定深度的网络来说,可以直接对每个隐藏层的滑动平均数据进行存储。但是对于RNN来说,网络的深度是变化的,如果使用BN的话,就需要存储不同时间步不同层的统计数据,这听起来似乎就不是很直观,且还有点复杂了。为此,引入LN直接对每一层的每个样本进行标准化,不再需要引入训练样本间的依赖性了,也不需要存储任何信息。
适用于需要使用递归神经网络的场景,对于视觉任务如果用LN取代BN,效果会变差,这是因为这并不符合CNN的假设,CNN每个通道的特征是学习出来的,相对独立的,将每个样本的所有通道联合起来进行标准化,就等同于把学习到的特征都抹去了,所以效果会变差。
Instance Normalization
IN直观上来讲就是对每张图像的每个通道进行标准化,这实际上就是对每张图像进行亮度和对比度的调整,经过标准化后,就相当于去除掉了图像的亮度和对比度信息。
目前,IN一般应用于图像风格转换任务,在该任务中,我们要将风格图像的风格(颜色、纹理等)与内容图像的内容相结合,那么我们就希望内容图像的风格不要影响到风格图像,所以IN应运而生,也确实与任务的需求相吻合。
Group Normalization
目前计算机视觉中很多任务(检测,分割,视频等)由于存储限制,只能使用很小的batch进行训练,而BN随着batch越来越小,效果是越来越差的。这是因为越小的batch,其统计的均值和方差就越不准确。由此引入GN,和LN,IN一样,要独立于batch的维度来进行normalization。
GN的核心思想就是引入group的概念,将channel划分成不同的group,在group内求均值和方差。如果group为1,那么GN就等同于LN。同理group等于通道数的话,那么GN等于IN。
LN和IN在视觉任务中效果并不好,但是GN效果不错,由此可见group的设定很重要。它也符合我们对于CNN的假设,深度网络每层的通道数是很多的,尤其到了网络的深层。可以想象这么多特征,特征与特征之间其实是有一定的微妙关系的,有些很相关,其特征分布很相似,有些就大相径庭。group的想法,其实就类似于特征聚类,让网络通过学习将相似相关的特征集中学习到一个group里,然后进行标准化,很合情合理。
这里其实顺理成章的就想到了BN和GN的结合,它们对于CNN的假设都是友好的,合理的,如果能将两者结合,是不是会效果更好呢?博主没有做过相关实验,就说到这儿了。
