神经网络——深度学习应用于计算机视觉

深度学习应用于计算机视觉

本章将介绍卷积神经网络，也叫 convnet，它是计算机视觉应用几乎都在使用的一种深度学习模型。你将学到将卷积神经网络应用于图像分类问题，特别是那些训练数据集较小的问题。 如果你工作的地方并非大型科技公司，这也将是你最常见的使用场景。

1、卷积神经网络简介

我们将深入讲解卷积神经网络的原理，以及它在计算机视觉任务上为什么如此成功。但在此之前，我们先来看一个简单的卷积神经网络示例，即使用卷积神经网络对 MNIST 数字进行分类，这个任务用密集连接网络做过（当时的测试精度为 97.8%）。虽然本例中的卷积神经网络很简单，但其精度肯定会超过密集连接的网络。

下列代码将会展示一个简单的卷积神经网络。它是 Conv2D 层和 MaxPooling2D 层的堆叠。 很快你就会知道这些层的作用。

# 实例化一个小型的卷积神经网络
from keras import layers
from keras import models

model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))

重要的是，卷积神经网络接收形状为 (image_height, image_width, image_channels) 的输入张量（不包括批量维度）。本例中设置卷积神经网络处理大小为 (28, 28, 1) 的输入张量， 这正是 MNIST 图像的格式。我们向第一层传入参数 input_shape=(28, 28, 1) 来完成此设置。

我们来看一下目前卷积神经网络的架构。

model.summary()

'''
Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d (Conv2D)              (None, 26, 26, 32)        320       
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None, 13, 13, 32)        0         
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 11, 11, 64)        18496     
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 5, 5, 64)          0         
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 3, 3, 64)          36928     
=================================================================
Total params: 55,744
Trainable params: 55,744
Non-trainable params: 0
_________________________________________________________________
'''

可以看到，每个 Conv2D 层和 MaxPooling2D 层的输出都是一个形状为 (height, width, channels) 的 3D 张量。宽度和高度两个维度的尺寸通常会随着网络加深而变小。通道数量由传 入 Conv2D 层的第一个参数所控制（32 或 64）。

下一步是将最后的输出张量［大小为 (3, 3, 64)］输入到一个密集连接分类器网络中， 即 Dense 层的堆叠，你已经很熟悉了。这些分类器可以处理 1D 向量，而当前的输出是 3D 张量。 首先，我们需要将 3D 输出展平为 1D，然后在上面添加几个 Dense 层。

# 在卷积神经网络上添加分类器
model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10, activation='softmax'))

我们将进行 10 类别分类，最后一层使用带 10 个输出的 softmax 激活。现在网络的架构如下。

'''
Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d (Conv2D)              (None, 26, 26, 32)        320       
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None, 13, 13, 32)        0         
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 11, 11, 64)        18496     
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 5, 5, 64)          0         
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 3, 3, 64)          36928     
_________________________________________________________________
flatten (Flatten)            (None, 576)               0         
_________________________________________________________________
dense (Dense)                (None, 64)                36928     
_________________________________________________________________
dense_1 (Dense)              (None, 10)                650       
=================================================================
Total params: 93,322
Trainable params: 93,322
Non-trainable params: 0
_________________________________________________________________
'''

如你所见，在进入两个 Dense 层之前，形状 (3, 3, 64) 的输出被展平为形状 (576,) 的 向量。

下面我们在 MNIST 数字图像上训练这个卷积神经网络。我们将复用前面 MNIST 示例中的很多代码。

# 在 MNIST 图像上训练卷积神经网络
from keras.datasets import mnist
from keras.utils import to_categorical

(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

train_images = train_images.reshape((60000, 28, 28, 1))
train_images = train_images.astype('float32') / 255

test_images = test_images.reshape((10000, 28, 28, 1))
test_images = test_images.astype('float32') / 255

train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)

# 拟合模型
model.compile(optimizer='rmsprop',
              loss='categorical_crossentropy',
              metrics=['accuracy'])
model.fit(train_images, train_labels, epochs=5, batch_size=64)

Epoch 1/5
938/938 [==============================] - 16s 17ms/step - loss: 0.1744 - accuracy: 0.9453
Epoch 2/5
938/938 [==============================] - 16s 17ms/step - loss: 0.0488 - accuracy: 0.9848
Epoch 3/5
938/938 [==============================] - 16s 17ms/step - loss: 0.0336 - accuracy: 0.9900
Epoch 4/5
938/938 [==============================] - 16s 17ms/step - loss: 0.0247 - accuracy: 0.9926
Epoch 5/5
938/938 [==============================] - 24s 26ms/step - loss: 0.0192 - accuracy: 0.9939

我们在测试数据上对模型进行评估。

# 在测试数据上对模型进行评估
test_loss, test_acc = model.evaluate(test_images, test_labels)
# 313/313 [==============================] - 2s 6ms/step - loss: 0.0291 - accuracy: 0.9909
print(test_acc)
# 0.9908999800682068

密集连接网络的测试精度为 97.8%，但这个简单卷积神经网络的测试精度达到了 99.0%，我们将错误率降低了 68%（相对比例）。相当不错！

与密集连接模型相比，为什么这个简单卷积神经网络的效果这么好？要回答这个问题，我 们来深入了解 Conv2D 层和 MaxPooling2D 层的作用。

1.1、卷积运算

密集连接层和卷积层的根本区别在于，Dense 层从输入特征空间中学到的是全局模式（比如对于 MNIST 数字，全局模式就是涉及所有像素的模式），而卷积层学到的是局部模式（见下图），对于图像来说，学到的就是在输入图像的二维小窗口中发现的模式。在上面的例子中， 这些窗口的大小都是 3×3。

这个重要特性使卷积神经网络具有以下两个有趣的性质。

• 卷积神经网络学到的模式具有平移不变性（translation invariant）。卷积神经网络在图像右下角学到某个模式之后，它可以在任何地方识别这个模式，比如左上角。对于密集连接网络来说，如果模式出现在新的位置，它只能重新学习这个模式。这使得卷积神经网络在处理图像时可以高效利用数据（因为视觉世界从根本上具有平移不变性），它只需要更少的训练样本就可以学到具有泛化能力的数据表示。

• 卷积神经网络可以学到模式的空间层次结构（spatial hierarchies of patterns），见下图。 第一个卷积层将学习较小的局部模式（比如边缘），第二个卷积层将学习由第一层特征组成的更大的模式，以此类推。这使得卷积神经网络可以有效地学习越来越复杂、越来越抽象的视觉概念（因为视觉世界从根本上具有空间层次结构）。

  

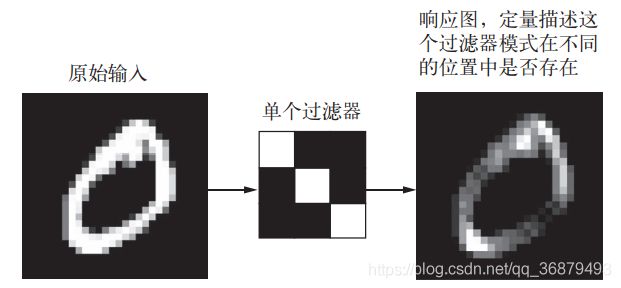
对于包含两个空间轴（高度和宽度）和一个深度轴（也叫通道轴）的 3D 张量，其卷积也叫特征图（feature map）。对于 RGB 图像，深度轴的维度大小等于 3，因为图像有 3 个颜色通道： 红色、绿色和蓝色。对于黑白图像（比如 MNIST 数字图像），深度等于 1（表示灰度等级）。卷积运算从输入特征图中提取图块，并对所有这些图块应用相同的变换，生成输出特征图（output feature map）。该输出特征图仍是一个 3D 张量，具有宽度和高度，其深度可以任意取值，因为输出深度是层的参数，深度轴的不同通道不再像 RGB 输入那样代表特定颜色，而是代表过滤器 （filter）。过滤器对输入数据的某一方面进行编码，比如，单个过滤器可以从更高层次编码这样一个概念：“输入中包含一张脸。”

在 MNIST 示例中，第一个卷积层接收一个大小为 (28, 28, 1) 的特征图，并输出一个大小为 (26, 26, 32) 的特征图，即它在输入上计算 32 个过滤器。对于这 32 个输出通道，每个通道都包含一个 26×26 的数值网格，它是过滤器对输入的响应图（response map），表示这个过滤器模式在输入中不同位置的响应（见下图）。这也是特征图这一术语的含义：深度轴的每个维度都是一个特征（或过滤器），而 2D 张量 output[:, :, n] 是这个过滤器在输入上的响应的二维空间图（map）。

卷积由以下两个关键参数所定义。

• 从输入中提取的图块尺寸：这些图块的大小通常是 3×3 或 5×5。本例中为 3×3，这是很常见的选择。
• 输出特征图的深度：卷积所计算的过滤器的数量。本例第一层的深度为 32，最后一层的深度是 64。

对于 Keras 的 Conv2D 层，这些参数都是向层传入的前几个参数：Conv2D(output_depth, (window_height, window_width))。

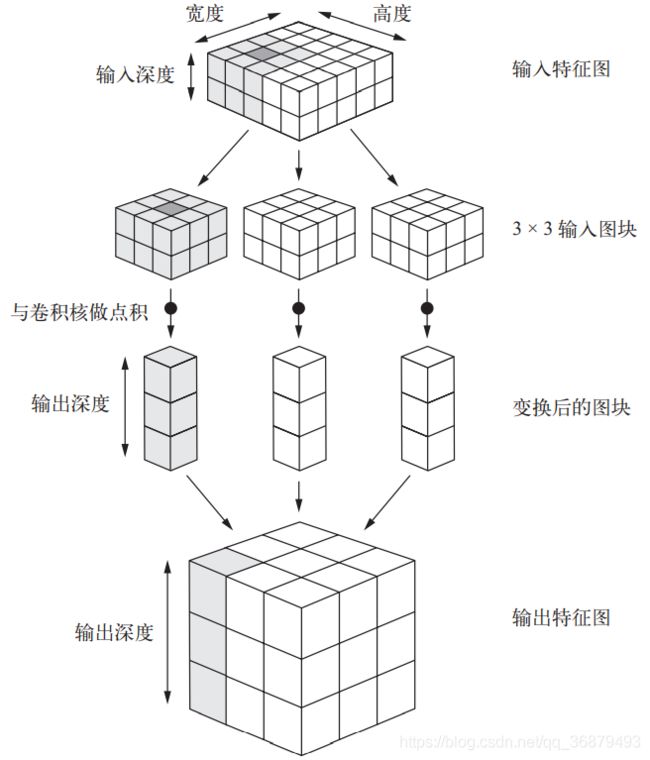
卷积的工作原理：在 3D 输入特征图上滑动（slide）这些 3×3 或 5×5 的窗口，在每个可能的位置停止并提取周围特征的 3D 图块［形状为 (window_height, window_width, input_ depth)］。然后每个 3D 图块与学到的同一个权重矩阵［叫作卷积核（convolution kernel）］做张量积，转换成形状为 (output_depth,) 的 1D 向量。然后对所有这些向量进行空间重组， 使其转换为形状为 (height, width, output_depth) 的 3D 输出特征图。输出特征图中的每个空间位置都对应于输入特征图中的相同位置（比如输出的右下角包含了输入右下角的信 息）。举个例子，利用 3×3 的窗口，向量 output[i, j, :] 来自 3D 图块 input[i-1:i+1, j-1:j+1, :]。整个过程详见下图。

注意，输出的宽度和高度可能与输入的宽度和高度不同。不同的原因可能有两点。

• 边界效应，可以通过对输入特征图进行填充来抵消。
• 使用了步幅（stride），稍后会给出其定义。

我们来深入研究一下这些概念。

1. 理解边界效应与填充

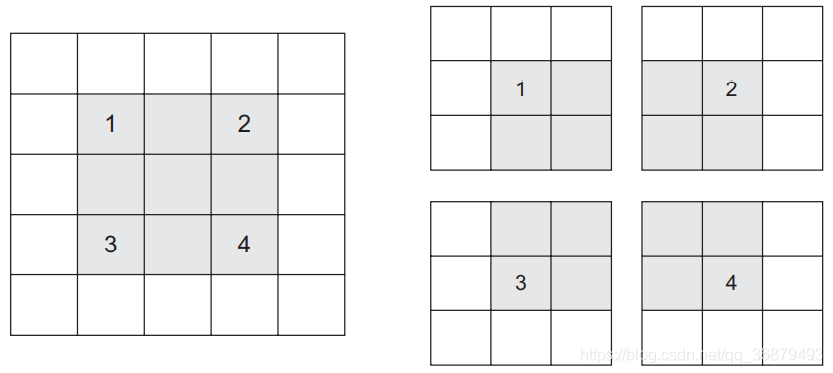
   假设有一个 5×5 的特征图（共 25 个方块）。其中只有 9 个方块可以作为中心放入一个 3×3 的窗口，这 9 个方块形成一个 3×3 的网格（见下图）。因此，输出特征图的尺寸是 3×3。 它比输入尺寸小了一点，在本例中沿着每个维度都正好缩小了 2 个方块。在前一个例子中你也可以看到这种边界效应的作用：开始的输入尺寸为 28×28，经过第一个卷积层之后尺寸变为 26×26。

   

   如果你希望输出特征图的空间维度与输入相同，那么可以使用填充（padding）。填充是在输入特征图的每一边添加适当数目的行和列，使得每个输入方块都能作为卷积窗口的中心。对于 3×3 的窗口，在左右各添加一列，在上下各添加一行。对于 5×5 的窗口，各添加两行和两列（见下图）。

   

   对于 Conv2D 层，可以通过 padding 参数来设置填充，这个参数有两个取值：“valid” 表示不使用填充（只使用有效的窗口位置）；“same” 表示 “填充后输出的宽度和高度与输入相同”。 padding 参数的默认值为 “valid”。

2. 理解卷积步幅

   影响输出尺寸的另一个因素是步幅的概念。目前为止，对卷积的描述都假设卷积窗口的中心方块都是相邻的。但两个连续窗口的距离是卷积的一个参数，叫作步幅，默认值为 1。也可以使用步进卷积（strided convolution），即步幅大于 1 的卷积。在下图中，你可以看到用步幅为 2 的 3×3 卷积从 5×5 输入中提取的图块（无填充）。

   

   步幅为 2 意味着特征图的宽度和高度都被做了 2 倍下采样（除了边界效应引起的变化）。虽 然步进卷积对某些类型的模型可能有用，但在实践中很少使用。熟悉这个概念是有好处的。

   为了对特征图进行下采样，我们不用步幅，而是通常使用最大池化（max-pooling）运算， 你在第一个卷积神经网络示例中见过此运算。下面我们来深入研究这种运算。

1.2、最大池化运算

在卷积神经网络示例中，你可能注意到，在每个 MaxPooling2D 层之后，特征图的尺寸都会减半。例如，在第一个 MaxPooling2D 层之前，特征图的尺寸是 26×26，但最大池化运算将其减半为 13×13。这就是最大池化的作用：对特征图进行下采样，与步进卷积类似。

**最大池化是从输入特征图中提取窗口，并输出每个通道的最大值。**它的概念与卷积类似， 但是最大池化使用硬编码的 max 张量运算对局部图块进行变换，而不是使用学到的线性变换（卷积核）。最大池化与卷积的最大不同之处在于，最大池化通常使用 2×2 的窗口和步幅 2，其目的是将特征图下采样 2 倍。与此相对的是，卷积通常使用 3×3 窗口和步幅 1。

为什么要用这种方式对特征图下采样？为什么不删除最大池化层，一直保留较大的特征图？ 我们来这么做试一下。这时模型的卷积基（convolutional base）如下所示。

# 最大池化运算的一个举例
from keras import layers
from keras import models

model_no_max_pool = models.Sequential()
model_no_max_pool.add(layers.Conv2D(32, (3, 3), activation='relu',
 input_shape=(28, 28, 1)))
model_no_max_pool.add(layers.Conv2D(64, (3, 3), activation='relu'))
model_no_max_pool.add(layers.Conv2D(64, (3, 3), activation='relu'))

model_no_max_pool.summary()
'''
Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d (Conv2D)              (None, 26, 26, 32)        320       
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 24, 24, 64)        18496     
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 22, 22, 64)        36928     
=================================================================
Total params: 55,744
Trainable params: 55,744
Non-trainable params: 0
_________________________________________________________________
'''

这种架构有什么问题？有如下两点问题。

• 这种架构不利于学习特征的空间层级结构。第三层的 3×3 窗口中只包含初始输入的 7×7 窗口中所包含的信息。卷积神经网络学到的高级模式相对于初始输入来说仍然很小， 这可能不足以学会对数字进行分类（你可以试试仅通过 7 像素×7 像素的窗口观察图像来识别其中的数字）。我们需要让最后一个卷积层的特征包含输入的整体信息。
• 最后一层的特征图对每个样本共有 22×22×64=30 976 个元素。这太多了。如果你将其展平并在上面添加一个大小为 512 的 Dense 层，那一层将会有 1580 万个参数。这对于这样一个小模型来说太多了，会导致严重的过拟合。

简而言之，使用下采样的原因，一是减少需要处理的特征图的元素个数，二是通过让连续卷积层的观察窗口越来越大（即窗口覆盖原始输入的比例越来越大），从而引入空间过滤器的层级结构。

注意，最大池化不是实现这种下采样的唯一方法。你已经知道，还可以在前一个卷积层中使用步幅来实现。此外，你还可以使用平均池化来代替最大池化，其方法是将每个局部输入图块变换为取该图块各通道的平均值，而不是最大值。但最大池化的效果往往比这些替代方法更好。 简而言之，原因在于特征中往往编码了某种模式或概念在特征图的不同位置是否存在（因此得名特征图），而观察不同特征的最大值而不是平均值能够给出更多的信息。因此，最合理的子采样策略是首先生成密集的特征图（通过无步进的卷积），然后观察特征每个小图块上的最大激活， 而不是查看输入的稀疏窗口（通过步进卷积）或对输入图块取平均，因为后两种方法可能导致错过或淡化特征是否存在的信息。

现在你应该已经理解了卷积神经网络的基本概念，即特征图、卷积和最大池化，并且也知道如何构建一个小型卷积神经网络来解决简单问题，比如 MNIST 数字分类。下面我们将介绍更加实用的应用。

---

2、在小型数据集上从头开始训练一个卷积神经网络

使用很少的数据来训练一个图像分类模型，这是很常见的情况，如果你要从事计算机视觉方面的职业，很可能会在实践中遇到这种情况。“很少的” 样本可能是几百张图像，也可能是几万张图像。来看一个实例，我们将重点讨论猫狗图像分类，数据集中包含 4000 张猫和狗的图像 （2000 张猫的图像，2000 张狗的图像）。我们将 2000 张图像用于训练，1000 张用于验证，1000 张用于测试。

本节将介绍解决这一问题的基本策略，即使用已有的少量数据从头开始训练一个新模型。 首先，在 2000 个训练样本上训练一个简单的小型卷积神经网络，不做任何正则化，为模型目标设定一个基准。这会得到 71% 的分类精度。此时主要的问题在于过拟合。然后，我们会介绍数据增强（data augmentation），它在计算机视觉领域是一种非常强大的降低过拟合的技术。使用数据增强之后，网络精度将提高到 82%。

之后还会介绍将深度学习应用于小型数据集的另外两个重要技巧：用预训练的网络做特征提取（得到的精度范围在 90% ~ 96%），对预训练的网络进行微调（最终精度为 97%）。总而言之， 这三种策略——从头开始训练一个小型模型、使用预训练的网络做特征提取、对预训练的网络进行微调——构成了你的工具箱，未来可用于解决小型数据集的图像分类问题。

2.1、深度学习与小数据问题的相关性

有时你会听人说，仅在有大量数据可用时，深度学习才有效。这种说法部分正确：深度学习的一个基本特性就是能够独立地在训练数据中找到有趣的特征，无须人为的特征工程，而这只在拥有大量训练样本时才能实现。对于输入样本的维度非常高（比如图像）的问题尤其如此。

但对于初学者来说，所谓 “大量” 样本是相对的，即相对于你所要训练网络的大小和深度而言。只用几十个样本训练卷积神经网络就解决一个复杂问题是不可能的，但如果模型很小， 并做了很好的正则化，同时任务非常简单，那么几百个样本可能就足够了。由于卷积神经网络学到的是局部的、平移不变的特征，它对于感知问题可以高效地利用数据。虽然数据相对较少， 但在非常小的图像数据集上从头开始训练一个卷积神经网络，仍然可以得到不错的结果，而且无须任何自定义的特征工程。本节你将看到其效果。

此外，深度学习模型本质上具有高度的可复用性，比如，已有一个在大规模数据集上训练的图像分类模型或语音转文本模型，你只需做很小的修改就能将其复用于完全不同的问题。特别是在计算机视觉领域，许多预训练的模型（通常都是在 ImageNet 数据集上训练得到的）现在都可以公开下载，并可以用于在数据很少的情况下构建强大的视觉模型。我们先来看一下数据。

2.2、下载数据

这个数据集包含 25 000 张猫狗图像（每个类别都有 12 500 张），大小为 543MB（压缩后）。 下载数据并解压之后，你需要创建一个新数据集，其中包含三个子集：每个类别各 1000 个样本 的训练集、每个类别各 500 个样本的验证集和每个类别各 500 个样本的测试集。

创建新数据集的代码如下所示。

import os, shutil

# The path to the directory where the original
# dataset was uncompressed
original_dataset_dir = 'G:\\practice\\python\\kaggle\\train'

# The directory where we will
# store our smaller dataset
base_dir = 'G:\\practice\\python\\kaggle\\cats_and_dogs_small'
os.mkdir(base_dir)

# Directories for our training,
# validation and test splits
train_dir = os.path.join(base_dir, 'train')
os.mkdir(train_dir)
validation_dir = os.path.join(base_dir, 'validation')
os.mkdir(validation_dir)
test_dir = os.path.join(base_dir, 'test')
os.mkdir(test_dir)

# Directory with our training cat pictures
train_cats_dir = os.path.join(train_dir, 'cats')
os.mkdir(train_cats_dir)

# Directory with our training dog pictures
train_dogs_dir = os.path.join(train_dir, 'dogs')
os.mkdir(train_dogs_dir)

# Directory with our validation cat pictures
validation_cats_dir = os.path.join(validation_dir, 'cats')
os.mkdir(validation_cats_dir)

# Directory with our validation dog pictures
validation_dogs_dir = os.path.join(validation_dir, 'dogs')
os.mkdir(validation_dogs_dir)

# Directory with our validation cat pictures
test_cats_dir = os.path.join(test_dir, 'cats')
os.mkdir(test_cats_dir)

# Directory with our validation dog pictures
test_dogs_dir = os.path.join(test_dir, 'dogs')
os.mkdir(test_dogs_dir)

# Copy first 1000 cat images to train_cats_dir
fnames = ['cat.{}.jpg'.format(i) for i in range(1000)]
for fname in fnames:
    src = os.path.join(original_dataset_dir, fname)
    dst = os.path.join(train_cats_dir, fname)
    shutil.copyfile(src, dst)

# Copy next 500 cat images to validation_cats_dir
fnames = ['cat.{}.jpg'.format(i) for i in range(1000, 1500)]
for fname in fnames:
    src = os.path.join(original_dataset_dir, fname)
    dst = os.path.join(validation_cats_dir, fname)
    shutil.copyfile(src, dst)

# Copy next 500 cat images to test_cats_dir
fnames = ['cat.{}.jpg'.format(i) for i in range(1500, 2000)]
for fname in fnames:
    src = os.path.join(original_dataset_dir, fname)
    dst = os.path.join(test_cats_dir, fname)
    shutil.copyfile(src, dst)

# Copy first 1000 dog images to train_dogs_dir
fnames = ['dog.{}.jpg'.format(i) for i in range(1000)]
for fname in fnames:
    src = os.path.join(original_dataset_dir, fname)
    dst = os.path.join(train_dogs_dir, fname)
    shutil.copyfile(src, dst)

# Copy next 500 dog images to validation_dogs_dir
fnames = ['dog.{}.jpg'.format(i) for i in range(1000, 1500)]
for fname in fnames:
    src = os.path.join(original_dataset_dir, fname)
    dst = os.path.join(validation_dogs_dir, fname)
    shutil.copyfile(src, dst)

# Copy next 500 dog images to test_dogs_dir
fnames = ['dog.{}.jpg'.format(i) for i in range(1500, 2000)]
for fname in fnames:
    src = os.path.join(original_dataset_dir, fname)
    dst = os.path.join(test_dogs_dir, fname)
    shutil.copyfile(src, dst)

我们来检查一下，看看每个分组（训练 / 验证 / 测试）中分别包含多少张图像。

print('total training cat images:', len(os.listdir(train_cats_dir)))
# total training cat images: 1000
print('total training dog images:', len(os.listdir(train_dogs_dir)))
# total training dog images: 1000
print('total validation cat images:', len(os.listdir(validation_cats_dir)))
# total validation cat images: 500
print('total validation dog images:', len(os.listdir(validation_dogs_dir)))
# total validation dog images: 500
print('total test cat images:', len(os.listdir(test_cats_dir)))
# total test cat images: 500
print('total test dog images:', len(os.listdir(test_dogs_dir)))
# total test dog images: 500

所以我们的确有 2000 张训练图像、1000 张验证图像和 1000 张测试图像。每个分组中两个类别的样本数相同，这是一个平衡的二分类问题，分类精度可作为衡量成功的指标。

2.3、构建网络

在前一个 MNIST 示例中，我们构建了一个小型卷积神经网络，所以你应该已经熟悉这种网络。我们将复用相同的总体结构，即卷积神经网络由 Conv2D 层（使用 relu 激活）和 MaxPooling2D 层交替堆叠构成。

但由于这里要处理的是更大的图像和更复杂的问题，你需要相应地增大网络，即再增加一 个 Conv2D+MaxPooling2D 的组合。这既可以增大网络容量，也可以进一步减小特征图的尺寸， 使其在连接 Flatten 层时尺寸不会太大。本例中初始输入的尺寸为 150×150（有些随意的选择），所以最后在 Flatten 层之前的特征图大小为 7×7。

注意

网络中特征图的深度在逐渐增大（从 32 增大到 128），而特征图的尺寸在逐渐减小（从 150×150 减小到 7×7）。这几乎是所有卷积神经网络的模式。

你面对的是一个二分类问题，所以网络最后一层是使用 sigmoid 激活的单一单元（大小为 1 的 Dense 层）。这个单元将对某个类别的概率进行编码。

# 将猫狗分类的小型卷积神经网络实例化

from keras import layers
from keras import models

model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu',
                        input_shape=(150, 150, 3)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Flatten())
model.add(layers.Dense(512, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

我们来看一下特征图的维度如何随着每层变化。

model.summary()
'''
Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d (Conv2D)              (None, 148, 148, 32)      896       
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None, 74, 74, 32)        0         
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 72, 72, 64)        18496     
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 36, 36, 64)        0         
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 34, 34, 128)       73856     
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 17, 17, 128)       0         
_________________________________________________________________
conv2d_3 (Conv2D)            (None, 15, 15, 128)       147584    
_________________________________________________________________
max_pooling2d_3 (MaxPooling2 (None, 7, 7, 128)         0         
_________________________________________________________________
flatten (Flatten)            (None, 6272)              0         
_________________________________________________________________
dense (Dense)                (None, 512)               3211776   
_________________________________________________________________
dense_1 (Dense)              (None, 1)                 513       
=================================================================
Total params: 3,453,121
Trainable params: 3,453,121
Non-trainable params: 0
_________________________________________________________________
'''

在编译这一步，和前面一样，我们将使用 RMSprop 优化器。因为网络最后一层是单一 sigmoid 单元，所以我们将使用二元交叉熵作为损失函数。

# 配置模型用于训练
from keras import optimizers

model.compile(loss='binary_crossentropy',
              optimizer=optimizers.RMSprop(lr=1e-4),
              metrics=['acc'])

2.4、数据预处理

你现在已经知道，将数据输入神经网络之前，应该将数据格式化为经过预处理的浮点数张量。 现在，数据以 JPEG 文件的形式保存在硬盘中，所以数据预处理步骤大致如下。

1. 读取图像文件；
2. 将 JPEG 文件解码为 RGB 像素网格；
3. 将这些像素网格转换为浮点数张量；
4. 将像素值（0~255 范围内）缩放到 [0, 1] 区间（正如你所见，神经网络喜欢处理这样较小的输入值）。

这些步骤可能看起来有点吓人，但幸运的是，Keras 拥有自动完成这些步骤的工具。Keras 有一个图像处理辅助工具的模块，位于 keras.preprocessing.image。特别地，它包含 ImageDataGenerator 类，可以快速创建 Python 生成器，能够将硬盘上的图像文件自动转换为预处理好的张量批量。下面我们将用到这个类。

# 使用 ImageDataGenerator 从目录中读取图像
from keras.preprocessing.image import ImageDataGenerator

# All images will be rescaled by 1./255
train_datagen = ImageDataGenerator(rescale=1./255)
test_datagen = ImageDataGenerator(rescale=1./255)

train_generator = train_datagen.flow_from_directory(
        # This is the target directory
        train_dir,
        # All images will be resized to 150x150
        target_size=(150, 150),
        batch_size=20,
        # Since we use binary_crossentropy loss, we need binary labels
        class_mode='binary')

validation_generator = test_datagen.flow_from_directory(
        validation_dir,
        target_size=(150, 150),
        batch_size=20,
        class_mode='binary')

理解 Python 生成器

Python 生成器（Python generator）是一个类似于迭代器的对象，一个可以和 for … in 运算符一起使用的对象。生成器是用 yield 运算符来构造的。

下面一个生成器的例子，可以生成整数。

def generator():
 	i=0
 	while True:
 		i += 1
 		yield i
 
 for item in generator():
 	print(item)
 	if item > 4:
 		break

输出结果如下。

1
2
3
4
5

我们来看一下其中一个生成器的输出：它生成了 150×150 的 RGB 图像［形状为 (20, 150, 150, 3)］与二进制标签［形状为 (20,)］组成的批量。每个批量中包含 20 个样本（批 量大小）。注意，生成器会不停地生成这些批量，它会不断循环目标文件夹中的图像。因此，你需要在某个时刻终止（break）迭代循环。

for data_batch, labels_batch in train_generator:
    print('data batch shape:', data_batch.shape)
    print('labels batch shape:', labels_batch.shape)
    break

data batch shape: (20, 150, 150, 3)
labels batch shape: (20,)

利用生成器，我们让模型对数据进行拟合。我们将使用 fit_generator 方法来拟合，它在数据生成器上的效果和 fit 相同。它的第一个参数应该是一个 Python 生成器，可以不停地生成输入和目标组成的批量，比如 train_generator。因为数据是不断生成的，所以 Keras 模型要知道每一轮需要从生成器中抽取多少个样本。这是 steps_per_epoch 参数的作用：从生成器中抽取 steps_per_epoch 个批量后（即运行了 steps_per_epoch 次梯度下降），拟合过程将进入下一个轮次。本例中，每个批量包含 20 个样本，所以读取完所有 2000 个样本需要 100 个批量。

使用 fit_generator 时，你可以传入一个 validation_data 参数，其作用和在 fit 方 法中类似。值得注意的是，这个参数可以是一个数据生成器，但也可以是 Numpy 数组组成的元组。如果向 validation_data 传入一个生成器，那么这个生成器应该能够不停地生成验证数据批量，因此你还需要指定 validation_steps 参数，说明需要从验证生成器中抽取多少个批次用于评估。

# 利用批量生成器拟合模型
history = model.fit_generator(
      train_generator,
      steps_per_epoch=100,
      epochs=30,
      validation_data=validation_generator,
      validation_steps=50)

Epoch 1/30
100/100 [==============================] - 30s 301ms/step - loss: 0.6817 - acc: 0.5420 - val_loss: 0.6578 - val_acc: 0.5980
Epoch 2/30
100/100 [==============================] - 30s 302ms/step - loss: 0.6389 - acc: 0.6220 - val_loss: 0.6675 - val_acc: 0.5960
Epoch 3/30
100/100 [==============================] - 30s 302ms/step - loss: 0.5922 - acc: 0.6735 - val_loss: 0.5982 - val_acc: 0.6680
Epoch 4/30
100/100 [==============================] - 32s 319ms/step - loss: 0.5599 - acc: 0.7075 - val_loss: 0.6065 - val_acc: 0.6620
Epoch 5/30
100/100 [==============================] - 32s 319ms/step - loss: 0.5363 - acc: 0.7270 - val_loss: 0.5885 - val_acc: 0.6790
Epoch 6/30
100/100 [==============================] - 32s 322ms/step - loss: 0.5075 - acc: 0.7470 - val_loss: 0.5752 - val_acc: 0.6960
Epoch 7/30
100/100 [==============================] - 32s 317ms/step - loss: 0.4950 - acc: 0.7690 - val_loss: 0.5670 - val_acc: 0.6930
Epoch 8/30
100/100 [==============================] - 32s 319ms/step - loss: 0.4568 - acc: 0.7830 - val_loss: 0.5512 - val_acc: 0.7140
Epoch 9/30
100/100 [==============================] - 48s 479ms/step - loss: 0.4273 - acc: 0.7980 - val_loss: 0.5330 - val_acc: 0.7280
Epoch 10/30
100/100 [==============================] - 53s 527ms/step - loss: 0.4097 - acc: 0.8125 - val_loss: 0.5585 - val_acc: 0.7120
Epoch 11/30
100/100 [==============================] - 53s 526ms/step - loss: 0.3777 - acc: 0.8340 - val_loss: 0.5456 - val_acc: 0.7260
Epoch 12/30
100/100 [==============================] - 52s 521ms/step - loss: 0.3583 - acc: 0.8400 - val_loss: 0.6046 - val_acc: 0.7040
Epoch 13/30
100/100 [==============================] - 52s 524ms/step - loss: 0.3372 - acc: 0.8515 - val_loss: 0.5640 - val_acc: 0.7240
Epoch 14/30
100/100 [==============================] - 52s 525ms/step - loss: 0.3143 - acc: 0.8645 - val_loss: 0.5997 - val_acc: 0.7220
Epoch 15/30
100/100 [==============================] - 52s 525ms/step - loss: 0.2936 - acc: 0.8785 - val_loss: 0.7024 - val_acc: 0.6960
Epoch 16/30
100/100 [==============================] - 53s 526ms/step - loss: 0.2786 - acc: 0.8875 - val_loss: 0.5482 - val_acc: 0.7380
Epoch 17/30
100/100 [==============================] - 53s 525ms/step - loss: 0.2496 - acc: 0.9010 - val_loss: 0.6000 - val_acc: 0.7310
Epoch 18/30
100/100 [==============================] - 52s 523ms/step - loss: 0.2335 - acc: 0.9110 - val_loss: 0.5786 - val_acc: 0.7450
Epoch 19/30
100/100 [==============================] - 53s 529ms/step - loss: 0.2081 - acc: 0.9220 - val_loss: 0.6560 - val_acc: 0.7460
Epoch 20/30
100/100 [==============================] - 53s 531ms/step - loss: 0.1879 - acc: 0.9300 - val_loss: 0.6891 - val_acc: 0.7270
Epoch 21/30
100/100 [==============================] - 53s 532ms/step - loss: 0.1707 - acc: 0.9410 - val_loss: 0.8710 - val_acc: 0.7010
Epoch 22/30
100/100 [==============================] - 53s 529ms/step - loss: 0.1592 - acc: 0.9405 - val_loss: 0.8242 - val_acc: 0.7210
Epoch 23/30
100/100 [==============================] - 53s 528ms/step - loss: 0.1425 - acc: 0.9590 - val_loss: 0.6899 - val_acc: 0.7460
Epoch 24/30
100/100 [==============================] - 52s 522ms/step - loss: 0.1168 - acc: 0.9600 - val_loss: 0.7340 - val_acc: 0.7360
Epoch 25/30
100/100 [==============================] - 53s 527ms/step - loss: 0.1100 - acc: 0.9670 - val_loss: 0.7563 - val_acc: 0.7320
Epoch 26/30
100/100 [==============================] - 52s 524ms/step - loss: 0.0993 - acc: 0.9675 - val_loss: 0.7509 - val_acc: 0.7530
Epoch 27/30
100/100 [==============================] - 52s 525ms/step - loss: 0.0845 - acc: 0.9750 - val_loss: 1.1076 - val_acc: 0.7010
Epoch 28/30
100/100 [==============================] - 52s 520ms/step - loss: 0.0710 - acc: 0.9775 - val_loss: 0.8252 - val_acc: 0.7340
Epoch 29/30
100/100 [==============================] - 52s 524ms/step - loss: 0.0599 - acc: 0.9850 - val_loss: 0.8578 - val_acc: 0.7490
Epoch 30/30
100/100 [==============================] - 52s 523ms/step - loss: 0.0506 - acc: 0.9855 - val_loss: 0.8733 - val_acc: 0.7450

始终在训练完成后保存模型，这是一种良好实践。

model.save('cats_and_dogs_small_1.h5')

我们来分别绘制训练过程中模型在训练数据和验证数据上的损失和精度。

# 绘制训练过程中的损失曲线和精度曲线

import matplotlib.pyplot as plt

acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']

epochs = range(len(acc))

plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()

plt.figure()

plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()

plt.show()

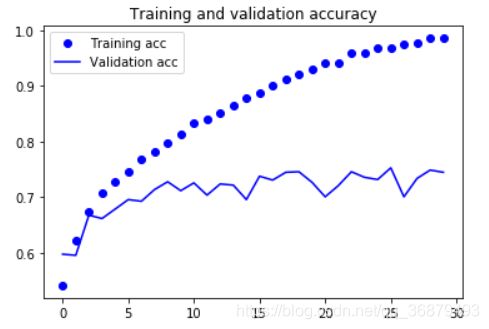
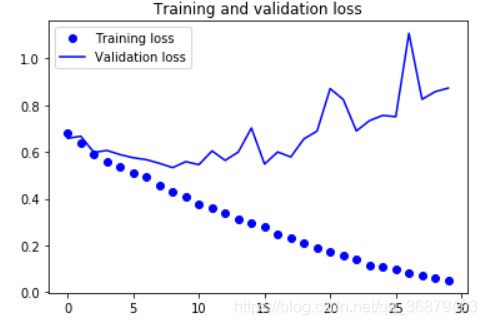
从这些图像中都能看出过拟合的特征。训练精度随着时间线性增加，直到接近 100%，而验证精度则停留在 70%~72%。验证损失仅在 5 轮后就达到最小值，然后保持不变，而训练损失则一直线性下降，直到接近于 0。

因为训练样本相对较少（2000 个），所以过拟合是你最关心的问题。前面已经介绍过几种降低过拟合的技巧，比如 dropout 和权重衰减（L2 正则化）。现在我们将使用一种针对于计算机视觉领域的新方法，在用深度学习模型处理图像时几乎都会用到这种方法，它就是数据增强 （data augmentation）。

2.5、使用数据增强

过拟合的原因是学习样本太少，导致无法训练出能够泛化到新数据的模型。如果拥有无限的数据，那么模型能够观察到数据分布的所有内容，这样就永远不会过拟合。数据增强是从现有的训练样本中生成更多的训练数据，其方法是利用多种能够生成可信图像的随机变换来增加 （augment）样本。其目标是，模型在训练时不会两次查看完全相同的图像。这让模型能够观察到数据的更多内容，从而具有更好的泛化能力。

在 Keras 中，这可以通过对 ImageDataGenerator 实例读取的图像执行多次随机变换来实现。我们先来看一个例子。

# 利用 ImageDataGenerator 来设置数据增强
datagen = ImageDataGenerator(
      rotation_range=40,
      width_shift_range=0.2,
      height_shift_range=0.2,
      shear_range=0.2,
      zoom_range=0.2,
      horizontal_flip=True,
      fill_mode='nearest')

这里只选择了几个参数（想了解更多参数，请查阅 Keras 文档）。我们来快速介绍一下这些参数的含义。

• rotation_range 是角度值（在 0~180 范围内），表示图像随机旋转的角度范围。
• width_shift 和 height_shift 是图像在水平或垂直方向上平移的范围（相对于总宽度或总高度的比例）。
• shear_range 是随机错切变换的角度。
• zoom_range 是图像随机缩放的范围。
• horizontal_flip 是随机将一半图像水平翻转。如果没有水平不对称的假设（比如真 实世界的图像），这种做法是有意义的。
• fill_mode是用于填充新创建像素的方法，这些新像素可能来自于旋转或宽度/高度平移。 我们来看一下增强后的图像（见下图）。

# This is module with image preprocessing utilities
from keras.preprocessing import image

fnames = [os.path.join(train_cats_dir, fname) for fname in os.listdir(train_cats_dir)]

# We pick one image to "augment"
img_path = fnames[3]

# Read the image and resize it
img = image.load_img(img_path, target_size=(150, 150))

# Convert it to a Numpy array with shape (150, 150, 3)
x = image.img_to_array(img)

# Reshape it to (1, 150, 150, 3)
x = x.reshape((1,) + x.shape)

# The .flow() command below generates batches of randomly transformed images.
# It will loop indefinitely, so we need to `break` the loop at some point!
i = 0
for batch in datagen.flow(x, batch_size=1):
    plt.figure(i)
    imgplot = plt.imshow(image.array_to_img(batch[0]))
    i += 1
    if i % 4 == 0:
        break

plt.show()

如果你使用这种数据增强来训练一个新网络，那么网络将不会两次看到同样的输入。但网络看到的输入仍然是高度相关的，因为这些输入都来自于少量的原始图像。你无法生成新信息， 而只能混合现有信息。因此，这种方法可能不足以完全消除过拟合。为了进一步降低过拟合， 你还需要向模型中添加一个 Dropout 层，添加到密集连接分类器之前。

# 定义一个包含 dropout 的新卷积神经网络

model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu',
                        input_shape=(150, 150, 3)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(128, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Flatten())
model.add(layers.Dropout(0.5))
model.add(layers.Dense(512, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

model.compile(loss='binary_crossentropy',
              optimizer=optimizers.RMSprop(lr=1e-4),
              metrics=['acc'])

# 利用数据增强生成器训练卷积神经网络

train_datagen = ImageDataGenerator(
    rescale=1./255,
    rotation_range=40,
    width_shift_range=0.2,
    height_shift_range=0.2,
    shear_range=0.2,
    zoom_range=0.2,
    horizontal_flip=True,)

# Note that the validation data should not be augmented!
test_datagen = ImageDataGenerator(rescale=1./255)

train_generator = train_datagen.flow_from_directory(
        # This is the target directory
        train_dir,
        # All images will be resized to 150x150
        target_size=(150, 150),
        batch_size=32,
        # Since we use binary_crossentropy loss, we need binary labels
        class_mode='binary')

validation_generator = test_datagen.flow_from_directory(
        validation_dir,
        target_size=(150, 150),
        batch_size=32,
        class_mode='binary')

history = model.fit_generator(
      train_generator,
      steps_per_epoch=100,
      epochs=100,
      validation_data=validation_generator,
      validation_steps=50)

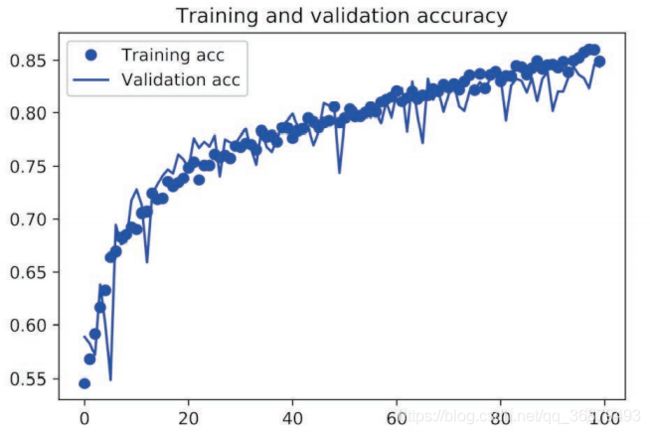
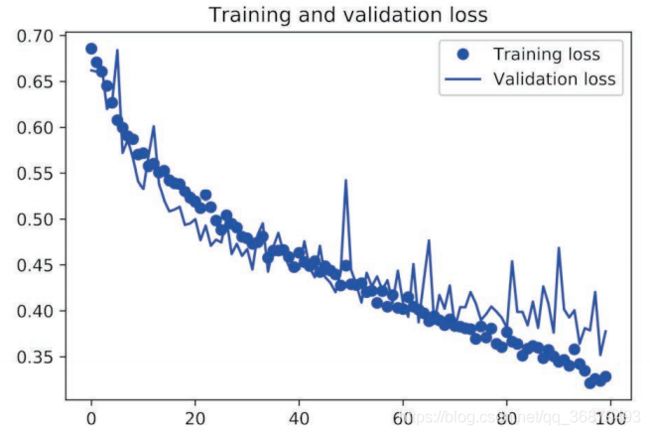
我们再次绘制结果。使用了数据增强和 dropout 之后，模型不再过拟合： 训练曲线紧紧跟随着验证曲线。现在的精度为 82%，比未正则化的模型提高了 15%（相对比例）。

通过进一步使用正则化方法以及调节网络参数（比如每个卷积层的过滤器个数或网络中的层数），你可以得到更高的精度，可以达到 86% 或 87%。但只靠从头开始训练自己的卷积神经网络， 再想提高精度就十分困难，因为可用的数据太少。想要在这个问题上进一步提高精度，下一步需要使用预训练的模型，这是接下来两节的重点。