学习数学建模算法与应用【回归分析】

前半部分为基础知识，后半部分为举例分析及MATLAB实践

一元线性回归

数学模型及定义

换句话说，也就是要使 所有样本点到样本回归 线的竖直距离的平方和最小。

模型参数估计

检验，预测及控制

可线性化的一元非线性回归

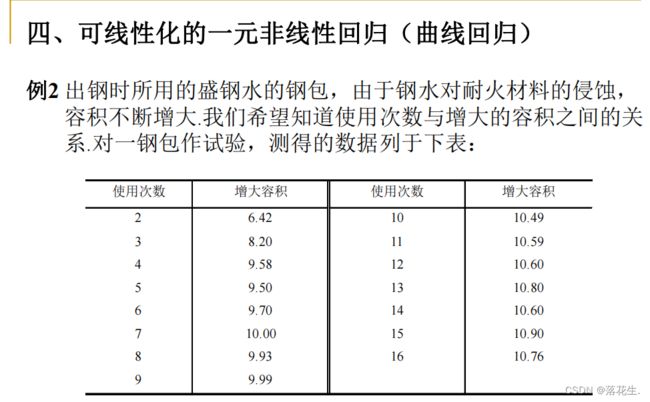
此即非线性回归或曲线回归 问题（需要配曲线）
配曲线的一般方法是：
先对两个变量x和y 作 n 次试验观察得(x;,y;),i=12,…,n 画出散点图根据散点图确定须配曲线的类型.然后由n对试验数据确定每一类曲线的未知参数 和b.采用的方法是通过变量代换把非线性回归化成线性回归，即采用非线性回归线性化的方法.

相关性分析和回归分析的区别
分析是否有相关关系，相关程度是多少；回归分析是构建表变量和变量之间具体的函数式，用函数或方程去拟合。
显著性水平：估计总体参数落在某一个区间整体犯错的概率，一般取5%

多元线性回归

回归命令分析及举例
1.多元线性回归
2.多项式回归
3.非线性回归
4.逐步回归

一、数学模型及定义

二、模型参数估计

三、多元线性回归中的检验与预测

四、逐步回归分析

“最优”的回归方程就是包含所有对Y有影响的变量, 而不包
含对Y影响不显著的变量回归方程. 选择“最优”的回归方程有以下几种方法：
（1）从所有可能的因子（变量）组合的回归方程中选择最优者；
（2）从包含全部变量的回归方程中逐次剔除不显著因子；
（3）从一个变量开始，把变量逐个引入方程；
（4）“有进有出”的逐步回归分析. 以第四种方法，即逐步回归分析法在筛选变量方面较
为理想

逐步回归分析法的思想：
• 从一个自变量开始，视自变量Y对作用的显著程度，从
大到小地依次逐个引入回归方程. • 当引入的自变量由于后面变量的引入而变得不显著时，
要将其剔除掉. • 引入一个自变量或从回归方程中剔除一个自变量，为
逐步回归的一步. • 对于每一步都要进行Y值检验，以确保每次引入新的显
著性变量前回归方程中只包含对Y作用显著的变量. • 这个过程反复进行，直至既无不显著的变量从回归方
程中剔除，又无显著变量可引入回归方程时为止

多元线性回归

解答
代码

%输入数据
x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]';
X=[ones(16,1) x];
Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]';
%回归分析与检验
[b,bint,r,rint,stats]=regress(Y,X)
rcoplot(r,rint)%做残差图
%图像的预测与对比
z=b(1)+b(2)*5%这里乘几都可以，只是为了做个对比。
plot(x,Y,'k+',x,z,'r')

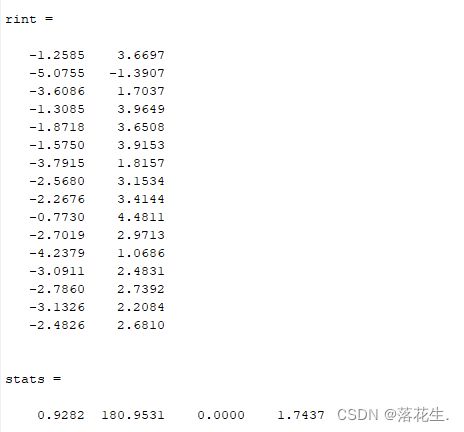
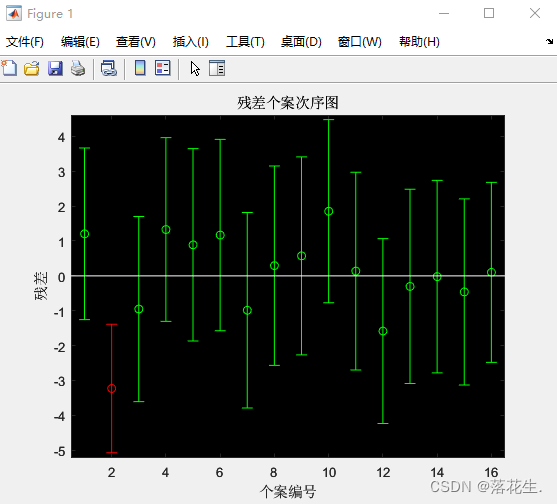
从残差图可以看出，除第二个数据外，其余数据的残差离零点均较近，且残差的置信区间均包含零点，这说明回归模型y-16.073+0.7194x能较好的符合原始数据，而第二个数据可视为异常点。

多项式回归

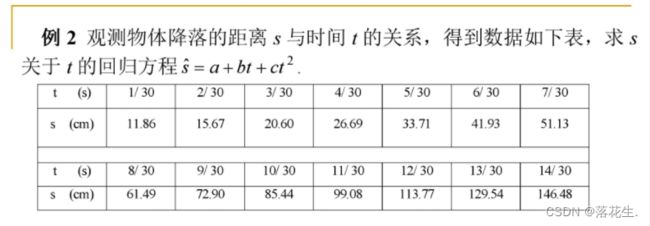
直接做二次多项式回归：

t=1/30:1/30:14/30;
s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49  72.90 85.44 99.08 113.77 129.54 146.48];
[p,S]=polyfit(t,s,2)%2指的是最高次数为2次

运行结果


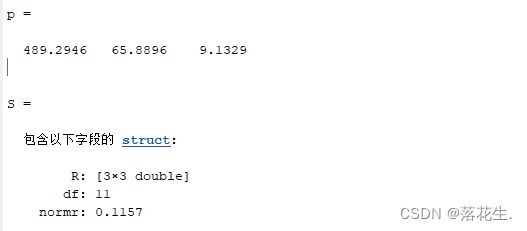
第二种方法：可以化做多元线性回归
将t²看成是一个元即x2，从而就变成了多元线性回归，来进行计算

%多项式回归化为多元线性回归
t=1/30:1/30:14/30;
s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];
T=[ones(14,1) t' (t.^2)'];%为14*3的矩阵
[b,bint,r,rint,stats]=regress(s',T);%回归系数，回归系数的区间估计，残差，置信期间
b,stats%回复系数和检验回归模型的统计量
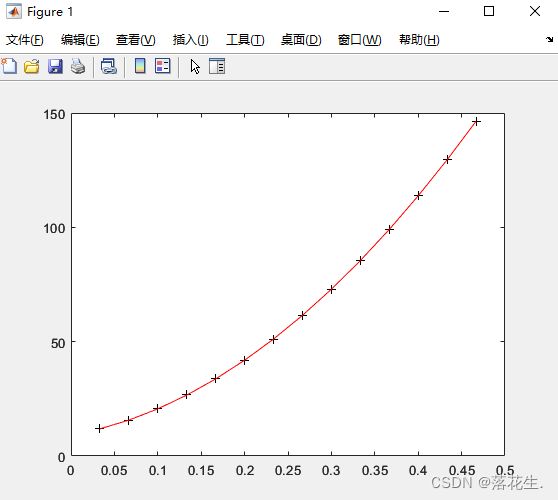
%预测及作图
Y=polyconf(p,t,S)%求回归多项式在x处的预测值Y
plot(t,s,'k+',t,Y,'r')

运行结果

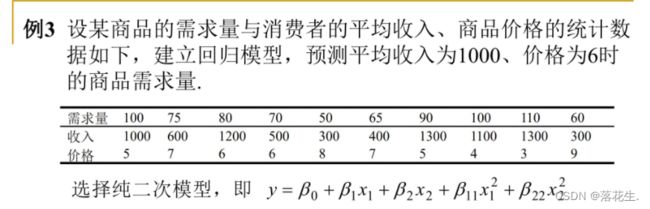
多元二项式回归

法一
直接用多元二项式回归
代码

x1=[1000 600 1200 500 300 400 1300 1100 1300 300];
x2=[5 7 6 6 8 7 5 4 3 9];
y=[100 75 80 70 50 65 90 100 110 60]';
x=[x1' x2'];
rstool(x,y,'purequadratic')%多元二项式回归，纯二次型

运行结果

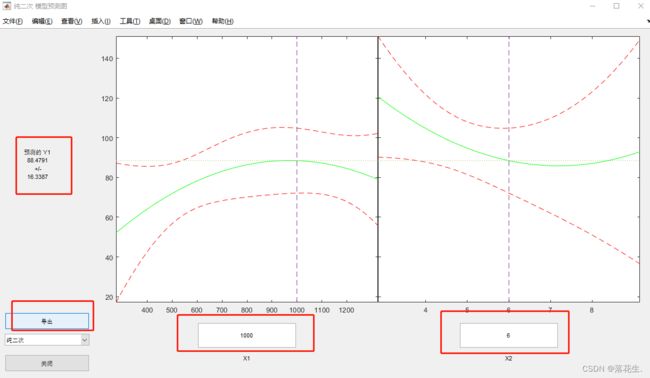
x1和x2处的值需要自己去手动更改，更改到自己需要的数值即可
左侧会显示预测结果
点击输出则beta．rmse和residuals都传送到MATLAB工作区中



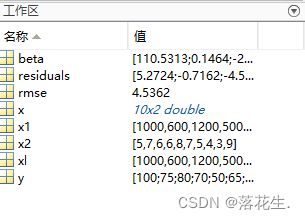
rmse一般小于10就可以。
法二：
将纯二次型转化为多元线性回归
代码

%多元二项式化为多元线性回归
x1=[1000 600 1200 500 300 400 1300 1100 1300 300];
x2=[5 7 6 6 8 7 5 4 3 9];
y=[100 75 80 70 50 65 90 100 110 60]';
x=[ones(10,1) x1' x2' (x1.^2)' (x2.^2)'];
[b,bint,r,rint,stats]=regress(y,x);
b,stats

运行结果

非线性回归

例题

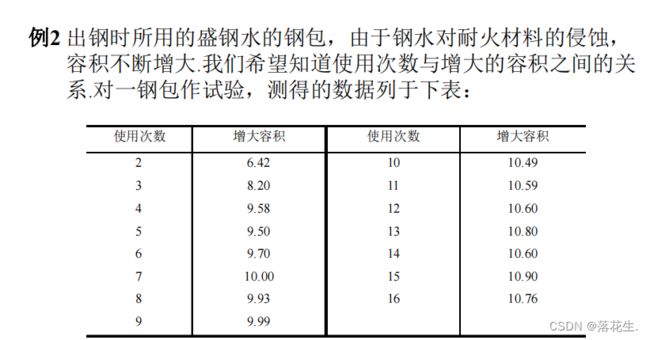
首先对将要拟合的非线性模型y=ae^b/x,建立M文件volum.m
代码

%非线性拟合
        %对将要拟合的非线性模型y=ae^b/x,建立M文件volum.m
        %function yhat=volum(beta,x)
        % yhat=beta(1)*exp(beta(2)./x);
%输入数据
x=2:16;
y=[6.42 8.20 9.58 9.5 9.7 10 9.93 9.99 10.49 10.59 10.60 10.80 10.60 10.90 10.76];
beta0=[8 2]';%初值
%求回归系数
[beta,r ,J]=nlinfit(x',y','volum',beta0);
beta

运行结果

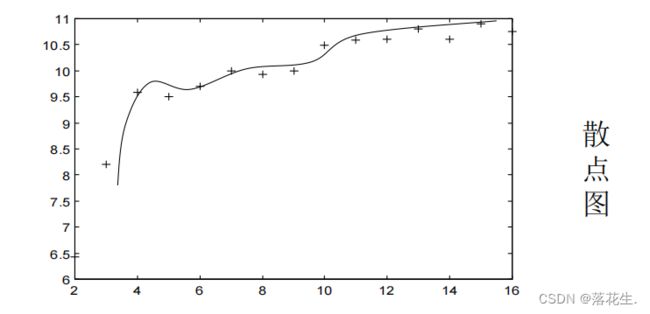
即得回归模型为：
y =11.6036e^-1.0641/x
图

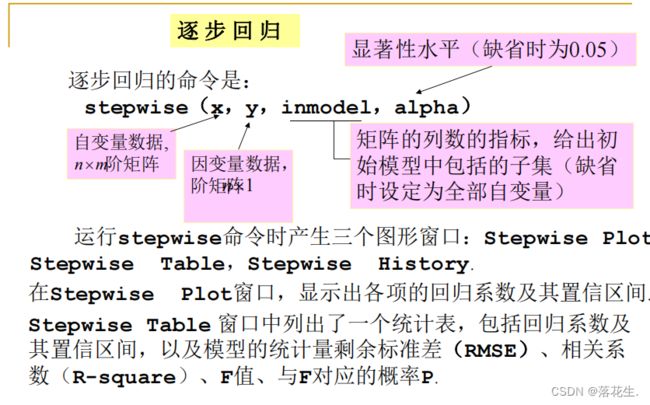
逐步回归

代码

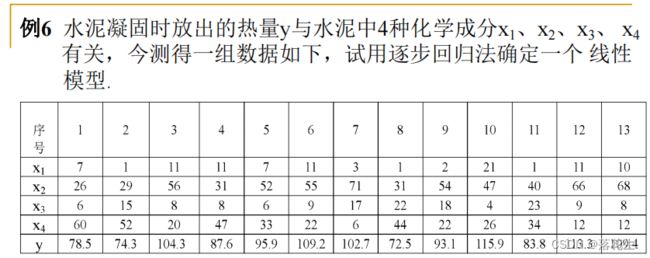
x1=[7 1 11 11 7 11 3 1 2 21 1 11 10]';
x2=[26 29 56 31 52 55 71 31 54 47 40 66 68]';
x3=[6 15 8 8 6 9 17 22 18 4 23 9 8]';
x4=[60 52 20 47 33 22 6 44 22 26 34 12 12]';
y=[78.5 74.3 104.3 87.6 95.9 109.2 102.7 72.5 93.1 115.9 83.8 113.3 109.4]';
x=[x1 x2 x3 x4];
stepwise(x,y)

运行结果

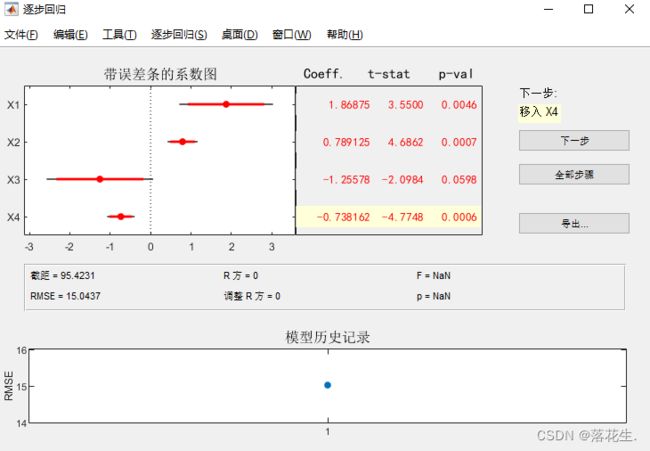
点击下一步，逐步移入各个变量，观察各个指标的变化，直到找到最合适的自变量组合
点击下一步，即移入x4观察结果

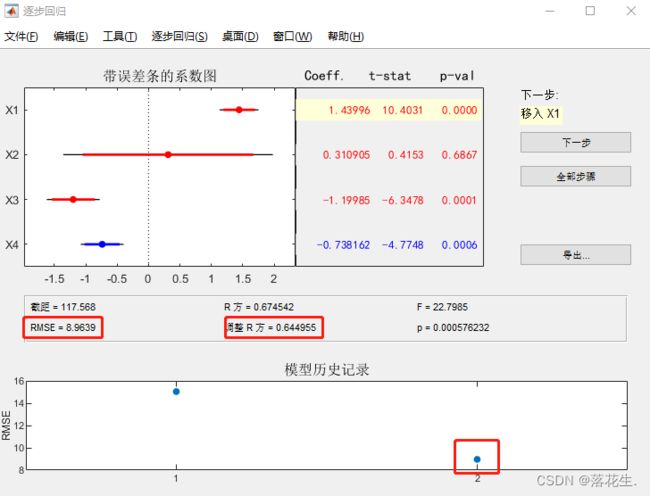
继续点击下一步，即移入x1观察结果，

可以看到RMSE经过这两步明显下降。相关系数明显提升，趋近于1。此时软件已经不能自己移入自变量了，不过魔门可以手动点击图中红线或者蓝线，自己去更改移入和移出自变量。
经过反复确认，将x1或x2移出时性能会发生显著变化，所以只保留x1和x2。
然后导出结果
导出的结果存放在工作区
输入代码

X=[ones(13,1) x1 x2];
b=regress(y,X)%对y,x1,x2做线性回归