人工智能与Python的渊源

人工智能起源与发展

---

---

前言

---

人工智能的发展，在近几年的发展中显的尤为重要，人工智能的涉及领域也不单单是机器人的领域，实际上，人工智能的研究领域包括图像识别，语音识别，自然语言处理，专家系统以及机器人技术等。

一、达特茅斯会议与人工智能起源

人工智能的起源公认为是1956年的达特茅斯会议，这次大会标志着“人工智能”这一概念的诞生。1955年，“人工智能”一词首在一份关于召开国际人工智能会议的提案中被提出，该提案由约翰·麦卡锡（John McCarthy，1971图灵奖得主），马文·明斯基（Marvin Minsky，1969年图灵奖得者），纳撒尼尔·罗彻斯特（Nathaniel Rochester，IBM第一代通用计算机701主设计师）和克劳德·香农（Claude Shannon，信息论之父）联合递交。

二、人工智能发展的高峰与低谷

人工智能的发展从1956年开始经历了三次高峰，两次低谷。目前正处于第三次的高峰期。
第一次高峰（1956——1972）来源于“感知器”的踢出，它解决了一些在当时看起来非常难的问题。在这之后，到1972年左右，由于计算能力和数据的限制，导致当时的技术难以解决实际的人工智能问题。而且数据库也难以满足人工智能的需要。同时，当时的人工智能框架也难以解决实际的问题，所以政府以及资助机构对人工智能研究失去了信心，纷纷撤资，这也就导致了人工智能的发展第一次进入低谷期。
1981年–1987年，人工智能的发展迎来第二次高峰期，专家系统和知识工程在全世界发展为企业和用户赢的巨大利益。特别是1986年Hopfield神经网络与BP算法的踢出，以及计算能力和存储能力的提升，使得大规模的神经网络的训练成为可能，由此将人工智能推入第二次高峰。但是到了20实际80年代末，金融危机的爆发，促使科学家对已有的人工智能思想和方法进行反思，特别是日本推广第五代计算机的失败，将人工智能引入第二个冬天。
20世纪90年代末，人工智能在各个领域快速发展。1997年，IBM制造的电脑“深蓝”击败了国际象棋世界冠军卡斯帕罗夫，这是人工智能的一次完美体现。2006年，杰弗里·辛顿首次提出了“深度学习”神经网络的概念，使的人工智能在领域内快速发展。

Python与人工智能

Python是由荷兰人吉多·范罗苏姆（Guido van Rossum）于1989年首次提出，第一个公开版本是在1991年发行。Python是纯粹的开源自由软件，源码和解析器均遵循GPL（GNU General Public License）协议。
OPython是一种多范式语言，他支持多种编程风格，包括脚本，面向对象等。Python的一个重要的特色就是跨平台，这意味着它可以在Windows，Linux，UNIX，macOS等不同操作系统上运行。但是，作为一个解释型语言，他的运行速度和C，C++等编译型语言有不小的差距。
由于Python语言对数据的操作性更简便，对图像，视频的操作相当简单，于是后面的文章我们均采用Python作为人工智能算法的例行语言。

构建Python人工智能编程环境

1.Python版本

python目前有两个版本，一个是Python2，另一个是Python3.Python2法比与2000年底，是使用较多的一个版本，官方声明，在2020年将停止对Python2的技术支持，所以后面的学习，我们将以Python3作为主要的编程环境。

2.Anaconda编程环境

Anaconda是一个开源的Python发行版本，其中集成了Conda，Python等180多个常用的数据处理和科学计算等工具包以及相关的依赖项。在后面的学习中会用到大量的外来安装包，为了简化这种安装的繁琐步骤，这里我们可以使用Anaconda编程环境。这里就不过多介绍，如果要下载，就直接搜索Anaconda官网进行下载，注意版本。下载过后，可以直接使用Anaconda所带的编程环境，也可以使用你以前的编译环境，将Anaconda中的Python解析器路径放到你用的编译器中即可。
Anaconda编程环境：

数据处理常用算法

2.1傅里叶变换

在信号处理领域，傅里叶变换（Fourier Transfom）可谓“大名鼎鼎”，它不仅是个数学工具，更像是一种“横看成林侧成峰”的哲学思维模式，让我们的思想在时域和频域的世界里面自由穿梭。傅里叶变换，本质上而言，是一个将时域非周期的连续信号转换为在频域非周期的连续信号的数学方法。

2.1.1傅里叶分析的由来

傅立叶是一位法国数学家和物理学家的名字，英语原名是Jean Baptiste Joseph Fourier（1768-1830），Fourier对热传递很感兴趣，于1807年在法国科学学会上发表了一篇论文，运用正弦曲线来描述温度分布，论文里有个在当时具有争议性的决断：任何连续周期信号可以由一组适当的正弦曲线组合而成。

当时审查这个论文的人，其中有两位是历史上著名的数学家拉格朗日（Joseph Louis Lagrange，1736-1813）和拉普拉斯（Pierre Simon de Laplace，1749-1827），当拉普拉斯和其它审查者投票通过并要发表这个论文时，拉格朗日坚决反对，在近50年的时间里，拉格朗日坚持认为傅立叶的方法无法表示带有棱角的信号，如在方波中出现非连续变化斜率。

法国科学学会屈服于拉格朗日的威望，拒绝了傅立叶的工作，幸运的是，傅立叶还有其它事情可忙，他参加了政治运动，随拿破仑远征埃及，法国大革命后因会被推上断头台而一直在逃避。直到拉格朗日死后15年，这个论文才被发表出来。

谁是对的呢？拉格朗日是对的：正弦曲线无法组合成一个带有棱角的信号。但是，我们可以用正弦曲线来非常逼近地表示它，逼近到两种表示方法不存在能量差别，基于此，傅立叶是对的。

2.1.2傅里叶变换原理及应用

傅里叶变换是一种信号分析，时域分析和频域分析是对信号分析的两个观察面。时域分析是以时间轴为坐标，表示动态信号的关系。频域分析是以频率作为坐标轴，描述频率变化于幅度变化。时域与频域的对应关系是：``时域图像中每一条正弦波曲线代表的简谐信号，在频域中对应一条谱线。

傅里叶公式

正弦波有一个其他波形（恒定的直流波形除外）所不具备的特点，那就是将正弦波输入任何一个线性系统，得到的依然是正弦波。仅幅值和相位会变化。且不会产生新的频率成分。这意味着，我们只需要研究正弦波的输入和输出关系，就可以知道该系统对输入信号的响应，这也是我们研究傅里叶变换的意义。
傅里叶变化的数学公式：
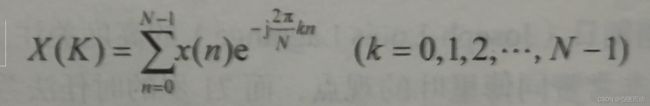其中X(K)表示离散傅里叶变换后的数据，x（n）为采样迷你数据。实际上，当x（n）为实际信号时，即虚部为0，则可以展开公式：

在进行数字信号分析的时候，傅里叶变换采样默认为等间隔采样，也就意味着无需时间序列而只需信号列表即可。进行傅里叶变换的基本步骤如下：

①.奈奎斯特采样定理（Nyquist Sampling Theorem）解释了采样频率和被测信号频率之间的关系。阐释了采样频率必须大于被测信号最高分量的两倍。该最高频率通常被称为奈奎斯特频率。亦即，对于含有m个样本值的数字信号序列，根据奈奎斯特采样定理，其中所包含的周期数最大为n/2（周期数为0代表直流分量）。因此，当周期数表示为离散序列0，1，2，3，4，5·······，n/2时，总数目为n/2+1个。
②.傅里叶变换后的结果为复数（complex），下标为k的复数a+bj表示时域信号中周期为N/k个取样值的正弦波和余弦波成分的多少，其中α表示余弦波的成分，b表示正弦波的成分。
③.产生一个长度为n的1倍周期的样本波形序列，该样本波形即为：
cos2Πkn/N - j *sin2Πkn/N
④.将数字信号序列中的每一个样本与1倍周期的样本波形序列相乘，得到n个乘积，并将乘积相加置于f[1]中。
⑤.继续类似步骤，产生一个长度为n，2倍周期的样本波形序列，再将数字信号序列中的每一个样本与该2倍周期样本波形序列相乘，得到n个乘积，并将乘积置于变量f[2]中，以此类推。
⑥.对于直流分量，亦即0倍周期样本波形，结果保存于变量f[0].

傅里叶变换代码展示

import numpy as np #主要用于信号处理相关操作
import matplotlib.pyplot as plt #主要用于数据可视化操作
def DFT(sig):
    t=np.linspace(0,1.0,len(sig)) #创建等间隔时间序列
    f=np.arange(len(sig)/2+1,dtype=complex)
    for index in range(len(f)):
        f[index]=complex(np.sum(np.cos(2*np.pi*index*t)*sig),-np.sum(np.sin(2*np.pi*index*t)*sig))
    return f
if __name__=='__main__':
    sampling_rate=1000 #采样率
    t=np.arange(0,1.0,1.0/sampling_rate) #时间轴
    N=30
    x=np.sin(N*np.pi*t) #定义信号，周期为T=2*pi/N*pi=1/15，概率为1/T=15
    x_ft=DFT(x)/len(x) #对信号进行傅里叶变换
    freqs=np.linspace(0,sampling_rate/2,int(len(x)/2+1))  #信号频率
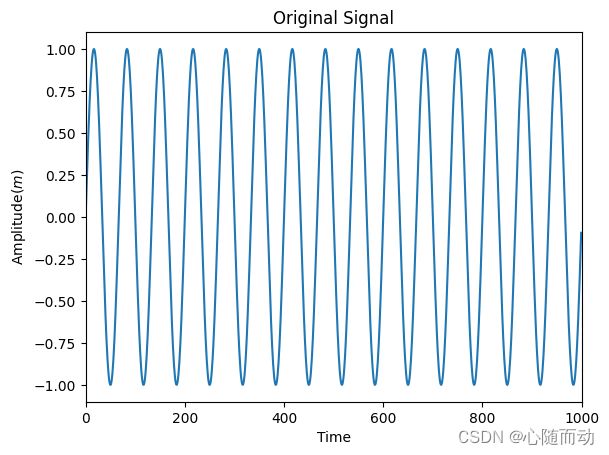
    #输出原正弦波信号
    plt.xlabel('Time')
    plt.ylabel('Amplitude($m$)')
    plt.title('Original Signal')
    plt.xlim(0,1000)
    plt.plot(x)
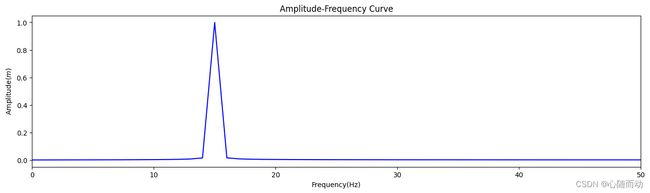
    #输出DFT后的信号频率，此处应为频率=15的幅率曲线
    plt.figure(figsize=(16,4))
    plt.plot(freqs,2*np.abs(x_ft),'b-')
    plt.xlabel('Frequency(Hz)')
    plt.ylabel('Amplitude($m$)')
    plt.title('Amplitude-Frequency Curve')
    plt.xlim(0,50)
    plt.show()

结果展示：

FFT算法

傅里叶分析因为其高效而频繁地使用于各种信号处理场合，因此，很多第三方Python模块，诸如Numpy和Scipy等，都内置了快速傅里叶变换（FFT）以及将信号从频域转换为时域的反快速傅里叶变换（IFFT）。为了我们更了解其相关函数，以下示例展示了一个包含3个人频率分量（120Hz,300Hz,500Hz）的混合样本波形经FFT变换后获取其频谱的过程，此处的傅里叶变换采用Scipy模块内置的FFT算法。示例代码如下：

import numpy as np
from scipy.fftpack import fft
import matplotlib.pyplot as plt
'''
根据奈奎斯特采样定理可知，采样率要大于2倍信号频率。故此采样率定为1000
'''
t=np.linspace(0,1,1000)
#定义正弦波信号，其中包含3个频率分量：120Hz，300Hz，500Hz
sig=7*np.sin(2*np.pi*120*t)+2.8*np.sin(2*np.pi*300*t)+5.1*np.sin(2*np.pi*500*t)
#对信号进行快速傅里叶变换，得到变换后的复数信号
sig_fft=fft(sig)
#对信号频谱取绝对值
abs_sig=abs(fft(sig))
#对信号进行归一化处理
normal_sig=abs(fft(sig))/len(t)
#根据信号的对称性，只取其中一半区间
half_sig=normal_sig[range(int(len(t)/2))]
x1=np.arange(len(sig))
x2=x1
x3=x1[range(int(len(t)/2))]
#显示原始信号
plt.subplot(221)
plt.plot(t[0:100],sig[0:100])
plt.title('Original wave')
#显示信号频谱的绝对值，滤除负信号频谱
plt.subplot(222)
plt.plot(x1,abs_sig,'b')
plt.title('Absolute Frequency Spectrum')
#显示归一化后的信号频谱
plt.subplot(223)
plt.plot(x2,normal_sig,'y')
plt.title('Normalized Frequency Spectrum')
#根据信号的对称性，显示半个区间的归一化信号频谱
plt.subplot(224)
plt.plot(x3,half_sig,'g')
plt.title('Half Normalized Frequency Spectrum')
plt.show()

结果展示：

总结

傅里叶变换的主题思想就是将时域转换为频域，这样可以很简单的将一些数据通过正弦函数的方式展现出来。本文介绍了傅里叶变换的相关知识，掌握好fft函数时本文的重点.