机器学习(李航统计学习方法)
目录
- 绪论-资料介绍
- 绪论-频率派vs贝叶斯派
-
- 频率派的观点
- 贝叶斯派的观点
- 监督学习与无监督学习
- 单变量线性回归
-
- 模型表示
- 代价函数
- 梯度下降
- 多变量线性回归
-
- 多维特征
- 多变量梯度下降
- 梯度下降法实践 1-特征缩放
- 梯度下降法实践 2-学习率
- 特征和多项式回归
- 正规方程
- 逻辑回归
-
- 分类问题
- 假说表示
- 判定边界
- 代价函数
- 简化的成本函数和梯度下降
- 高级优化
- 多类别分类:一对多
- 正则化
-
- 过拟合的问题
- 代价函数
- 正则化线性回归
- 正则化的逻辑回归模型
- 神经网络
-
- 非线性假设
- 模型表示1
- 模型表示2
- 特征和直观理解 1
- 特征和直观理解 2
- 神经网络的学习
-
- 代价函数
- 反向传播算法
- 反向传播算法的直观理解
- 实现注意:展开参数
- 梯度检验
- 随机初始化
- 综合起来
- 应用机器学习的建议
-
- 评估一个假设
- 模型选择和交叉验证集
- 诊断偏差和方差
- 正则化和偏差/方差
- 学习曲线
- 决定下一步做什么
- 机器学习系统的设计
-
- 首先要做什么
- 误差分析
- 类偏斜的误差度量
- 查准率和查全率之间的权衡
- 机器学习的数据
- 统计学习及监督学习概论
-
- 交叉验证
- 泛化能力
- 感知机
-
- 感知机模型
- 感知机学习策略
-
- 数据集的线性可分性
- 感知机学习策略
- 感知机学习算法
-
- 感知机学习算法的原始形式
- 感知机的对偶形式
- 本章概要
- 感知机代码理解
- k近邻法
-
- 1.1 k-近邻法简介
- 距离度量
- k近邻算法
- k近邻模型
- k近邻法的实现:kd树
- 本章概要
- 朴素贝叶斯法
-
- 朴素贝叶斯法的学习与分类
- 朴素贝叶斯法的参数估计
- 本章概要
- 决策树
-
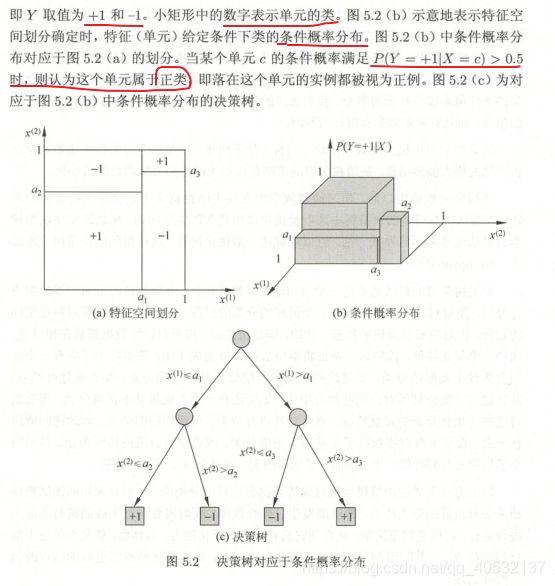
- 决策树模型与学习
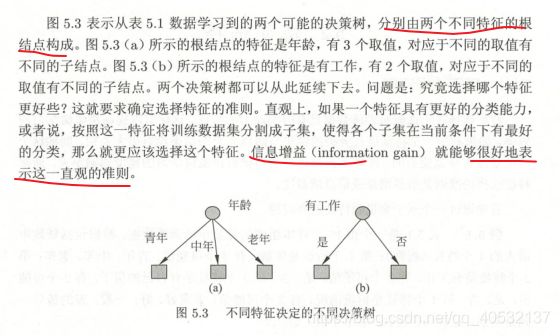
- 特征选择
- 决策树的生成
- 决策树的剪枝
- CART算法
- 本章概要
- 逻辑斯谛回归与最大熵模型
-
- 逻辑斯谛回归模型
- 最大熵模型
- 模型学习的最优化算法
- 支持向量机
-
- 线性可分支持向量机与间隔最大化
- 线性支持向量机与软间隔最大化
- 非线性支持向量机与核函数
- 序列最小最优化算法
- 本章概要
绪论-资料介绍
- 频率派->统计机器学习
- 贝叶斯派->概率图模型
书籍:统计学习方法,西瓜书,PRML,MLAPP,ESL,DeepLearning.
视频:台大的林轩田,基石,技法;张志华机器学习导论,统计机器学习;吴恩达cs229;徐亦达概率模型;台大李宏毅ML2017,MLDS2018;
绪论-频率派vs贝叶斯派
频率派的观点
∑:连加;∏:连乘;(A|):B条件下A的概率
MLE:极大似然估计
![]()
最大熵模型中的对数似然函数的解释:最大熵模型中的对数似然函数的解释
贝叶斯派的观点
贝叶斯:概率图模型,求积分
P(X| θ \theta θ):似然;P( θ \theta θ):先验概率;P( θ \theta θ|X):后验概率
MAP:最大后验概率估计
分母是积分所以是一个常量,所以整个值正比于分子

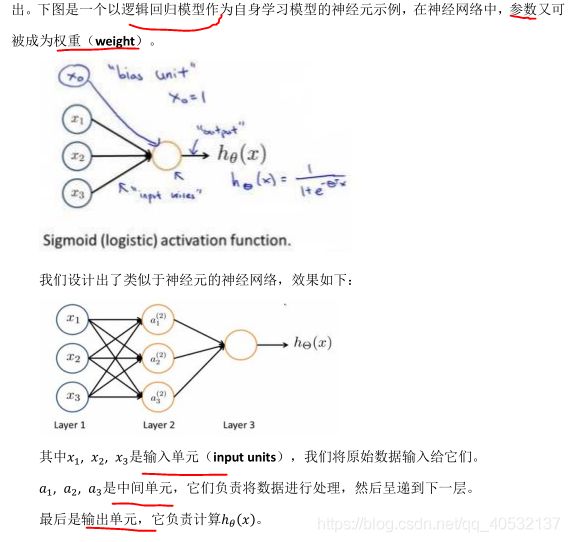
监督学习与无监督学习
监督学习:必须要有训练集与测试样本,在训练集中找规律,而对测试样本使用这种规律。
无监督学习:非监督学习没有训练集,只有一组数据,在该组数据集内寻找规律。
单变量线性回归
模型表示
例子是预测住房价格的,我们要使用一个数据集,数据集包含俄勒冈州波特兰市的住房价格。
一种可能的表达方式为:![]()
因为只含有一个特征/输入变量,因此这样的问题叫作单变量线性回归问题。
代价函数
代价函数 有助于我们弄清楚如何把最有可能的直线与我们的数据相拟合。
1.二维
模型所预测的值与训练集中实际值之间的差距(下图中蓝线所指)就是建模误差。
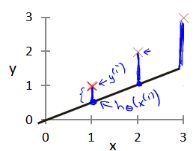
右图便是代价函数
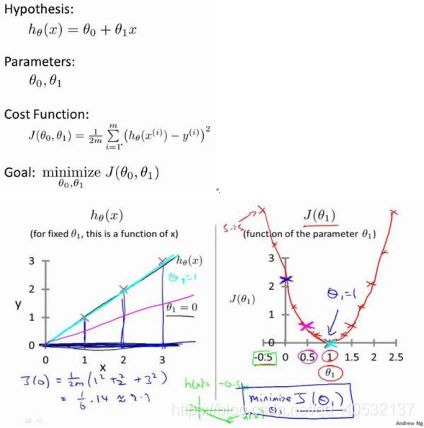
我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。 即使得代价
函数![]()
最小。
2.三维
我们绘制一个等高线图,三个坐标分别为0和1 和(0, 1):
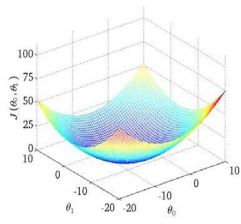
右图便是代价函数
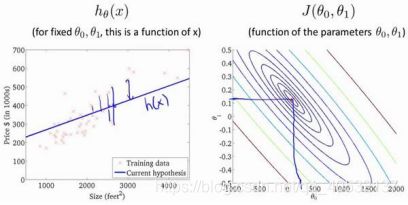
梯度下降
能够自动地找出能使代价函数 最小化的参数0和1的值。
批量梯度下降算法的公式为:
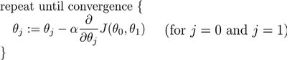

斜率越小,下降的越慢。斜率为0时,就不会下降。
多变量线性回归
多维特征
例子:对房价模型增加更多的特征,例如房间数楼层等,构成一个含有多个变量的模型,模型中的特征为(1,1, . . . , )。
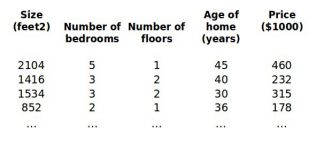
![]()
公式可以简化为:![]()
多变量梯度下降
我们也构建一个代价函数,则这个代价函数是所有建模误差的平方和,即:
![]()
其中:![]()
梯度下降法实践 1-特征缩放
面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛。
以房价问题为例,假设我们使用两个特征,房屋的尺寸和房间的数量,尺寸的值为 0-2000 平方英尺,而房间数量的值则是 0-5,以两个参数分别为横纵坐标,绘制代价函数的等高线图能,看出图像会显得很扁,梯度下降算法需要非常多次的迭代才能收敛。
解决的方法是尝试将所有特征的尺度都尽量缩放到-1 到 1 之间。

梯度下降法实践 2-学习率
梯度下降算法收敛所需要的迭代次数根据模型的不同而不同,我们不能提前预知,我们可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。
![]()
也有一些自动测试是否收敛的方法,例如将代价函数的变化值与某个阀值进行比较,但通常看上面这样的图表更好。
梯度下降算法的每次迭代受到学习率的影响,如果学习率过小,则达到收敛所需的迭代次数会非常高;如果学习率过大,每次迭代可能不会减小代价函数,可能会越过局部最小值导致无法收敛。 通常可以考虑尝试些学习率: = 0.01,0.03,0.1,0.3,1,3,10。
特征和多项式回归
如房价预测问题

线性回归并不适用于所有数据,有时我们需要曲线来适应我们的数据,比如一个二次方或者三次方。
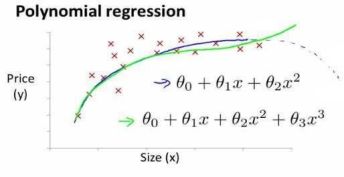
注:如果我们采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要。
正规方程
到目前为止,我们都在使用梯度下降算法,但是对于某些线性回归问题,正规方程方法是更好的解决方案。如:

总结一下,只要特征变量的数目并不大,标准方程是一个很好的计算参数的替代方法。具体地说,只要特征变量数量小于一万,我通常使用标准方程法,而不使用梯度下降法。
逻辑回归
分类问题
预测的变量 y是离散的值,我们将学习一种叫做逻辑回归算法。
二元的分类问题:将因变量可能属于的两个类分别称为负向类和正向类,则因变量 y∈0,1,其中 0 表示负向类,1 表示正向类。
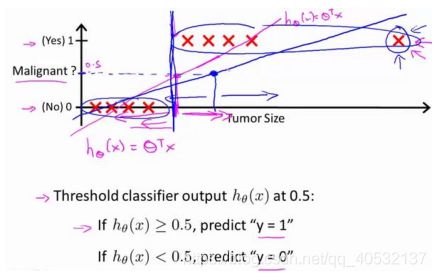
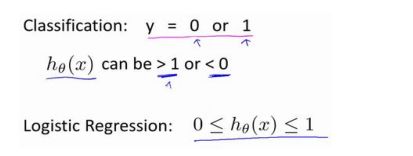
如果我们要用线性回归算法来解决一个分类问题,对于分类, 取值为 0 或者 1,但如果你使用的是线性回归,那么假设函数的输出值可能远大于 1,或者远小于 0,即使所有训练样本的标签 都等于 0 或 1。尽管我们知道标签应该取值 0 或者 1,但是如果算法得到的值远大于 1 或者远小于 0 的话,就会感觉很奇怪。所以我们在接下来的要研究的算法就叫做逻辑回归算法,这个算法的性质是:它的输出值永远在 0 到 1 之间。
顺便说一下,逻辑回归算法是分类算法,我们将它作为分类算法使用。有时候可能因为这个算法的名字中出现了“回归”使你感到困惑,但逻辑回归算法实际上是一种分类算法,它适用于标签 y 取值离散的情况,如:1 0 0 1。
假说表示
分类问题中,要用什么样的函数来表示我们的假设。此前我们说过,希望我们的分类器的输出值在 0 和 1 之间,因此,我们希望想出一个满足某个性质的假设函数,这个性质是它的预测值要在 0 和 1 之间。
根据线性回归模型我们只能预测连续的值,然而对于分类问题,我们需要输出 0 或 1,
我们可以预测:

可以看出,线性回归模型,因为其预测的值可以超越[0,1]的范围,并不适合解决这样的问题。
我们引入一个新的模型,逻辑回归,该模型的输出变量范围始终在 0 和 1 之间。 逻辑
回归模型的假设是:![]()
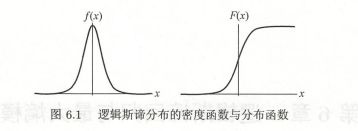
其中: X 代表特征向量 g 代表逻辑函数是一个常用的逻辑函数为 S 形函数,公式为:![]()
该函数的图像为:

例如,如果对于给定的,通过已经确定的参数计算得出ℎ (x) = 0.7,则表示有 70%的几率为正向类,相应地为负向类的几率为 1-0.7=0.3。
判定边界
现在讲下决策边界的概念。这个概念能更好地帮助我们理解逻辑回归的假设函数在计算什么。
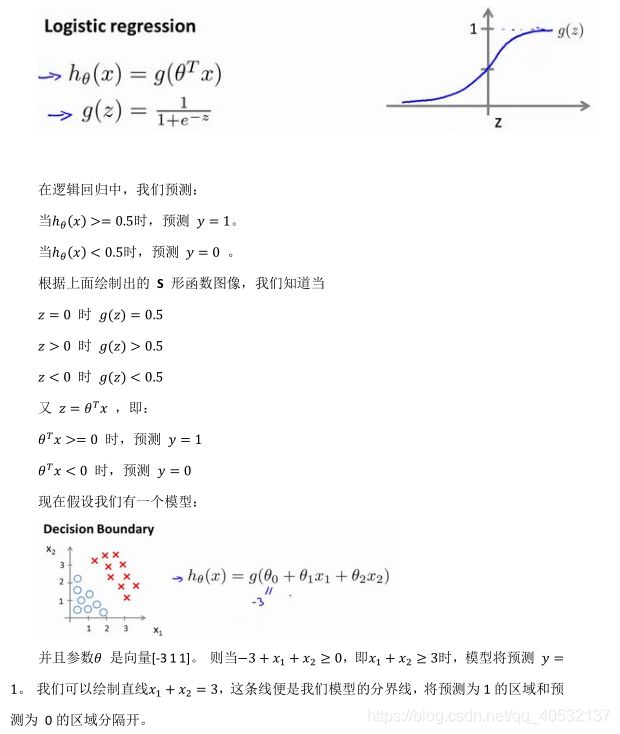
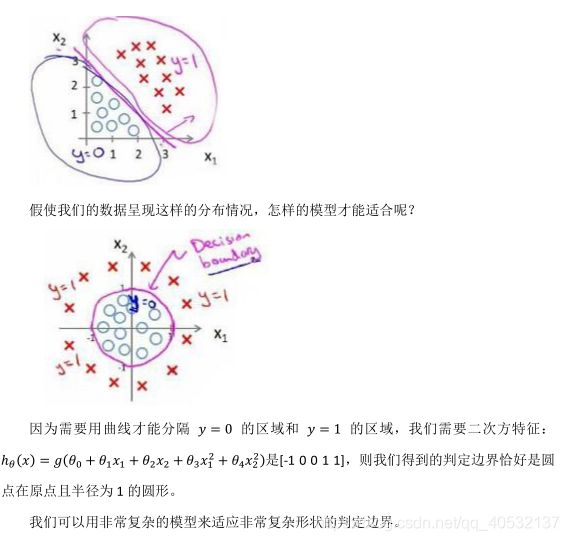
圆表达式:(x-a)²+(y-b)²=r² 。
代价函数
下面介绍如何拟合逻辑回归模型的参数 θ \theta θ。具体来说,我要定义用来拟合代价函数,这便是监督学习问题中的逻辑回归模型的拟合问题。
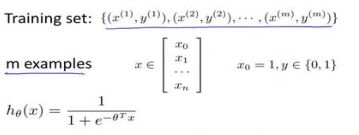
怎么选择参数 θ \theta θ?


在得到这样一个代价函数以后,我们便可以用梯度下降算法来求得能使代价函数最小的
参数了。算法为:
![]()

推导过程: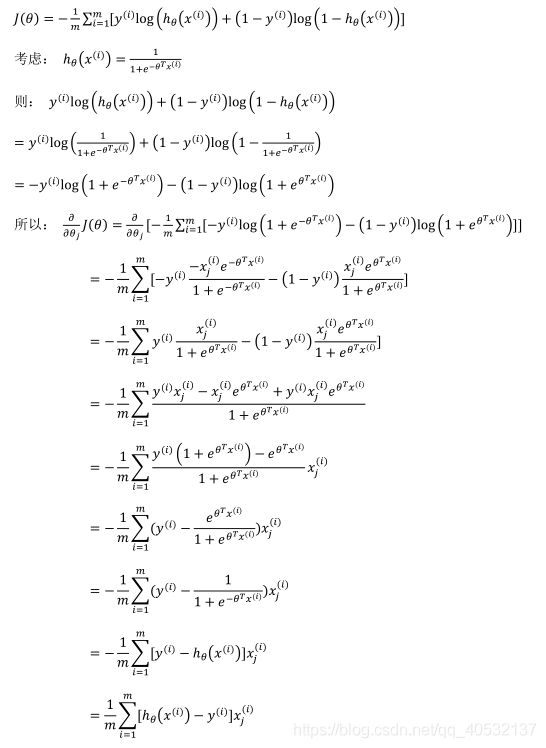


在下节中,我们会把单训练样本的代价函数的这些理念进一步发展,然后给出整个训练集的代价函数的定义,我们还会找到一种比我们目前用的更简单的写法,基于这些推导出的结果,我们将应用梯度下降法得到我们的逻辑回归算法。
简化的成本函数和梯度下降
我们将会找出一种稍微简单一点的方法来写代价函数,来替换我们现在用的方法。同时我们还要弄清楚如何运用梯度下降法,来拟合出逻辑回归的参数。因此看懂这节,你就应该知道如何实现一个完整的逻辑回归算法。

所以我们想要尽量减小这一项,这将我们将得到某个参数 θ \theta θ。
如果我们给出一个新的样本,假如某个特征 x,我们可以用拟合训练样本的参数 θ \theta θ,来
输出对假设的预测。
另外,我们假设的输出,实际上就是这个概率值:p(y = 1|x; θ \theta θ),就是关于 x以 θ \theta θ为参
数,y = 1 的概率,你可以认为我们的假设就是估计 y = 1 的概率,所以,接下来就是弄清楚如何最大限度地最小化代价函数J( θ \theta θ),作为一个关于 θ \theta θ的函数,这样我们才能为训练集拟合出参数 θ \theta θ。
最小化代价函数的方法,是使用梯度下降法。这是我们的代价函数:
![]()
如果我们要最小化这个关于 θ \theta θ的函数值,这就是我们通常用的梯度下降法的模板。

现在,如果你把这个更新规则和我们之前用在线性回归上的进行比较的话,你会惊讶地
发现,这个式子正是我们用来做线性回归梯度下降的。
那么,线性回归和逻辑回归是同一个算法吗?要回答这个问题,我们要观察逻辑回归看
看发生了哪些变化。实际上,假设的定义发生了变化。
对于线性回归假设函数:
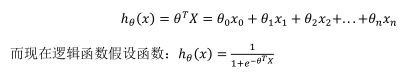
因此,即使更新参数的规则看起来基本相同,但由于假设的定义发生了变化,所以逻辑函数的梯度下降,跟线性回归的梯度下降实际上是两个完全不同的东西。
当我们在谈论线性回归的梯度下降法时,我们谈到了如何监控梯度下降法以确保其收敛,我通常也把同样的方法用在逻辑回归中,来监测梯度下降,以确保它正常收敛。
因此,即使更新参数的规则看起来基本相同,但由于假设的定义发生了变化,所以逻辑函数的梯度下降,跟线性回归的梯度下降实际上是两个完全不同的东西。
当我们在谈论线性回归的梯度下降法时,我们谈到了如何监控梯度下降法以确保其收敛,我通常也把同样的方法用在逻辑回归中,来监测梯度下降,以确保它正常收敛。
当使用梯度下降法来实现逻辑回归时,我们有这些不同的参数 θ \theta θ,就是 θ \theta θ 0 θ \theta θ 1 θ \theta θ 2 一直到 θ \theta θ n ,我们需要用这个表达式来更新这些参数。我们还可以使用 for 循环来更新这些参数值,用 for i=1 to n ,或者 for i=1 to n+1 。当然,不用 for 循环也是可以的,理想情况下,我们更提倡使用向量化的实现,可以把所有这些 n 个参数同时更新。
最后还有一点,我们之前在谈线性回归时讲到的特征缩放,我们看到了特征缩放是如何提高梯度下降的收敛速度的,这个特征缩放的方法,也适用于逻辑回归。如果你的特征范围差距很大的话,那么应用特征缩放的方法,同样也可以让逻辑回归中,梯度下降收敛更快。
就是这样,现在你知道如何实现逻辑回归,这是一种非常强大,甚至可能世界上使用最广泛的一种分类算法。
高级优化
在上节中,我们讨论了用梯度下降的方法最小化逻辑回归中代价函数J( θ \theta θ)。在本节中,学一些高级优化算法和一些高级的优化概念,利用这些方法,我们就能够使通过梯度下降,进行逻辑回归的速度大大提高,而这也将使算法更加适合解决大型的机器学习问题,比如,我们有数目庞大的特征量。
现在我们换个角度来看什么是梯度下降,我们有个代价函数J( θ \theta θ),而我们想要使其最小化,那么我们需要做的是编写代码,当输入参数 θ \theta θ时,它们会计算出两样东西:J( θ \theta θ) 以及J 等于 0、1 直到 n 时的偏导数项。

假设我们已经完成了可以实现这两件事的代码,那么梯度下降所做的就是反复执行这些更新。
另一种考虑梯度下降的思路是:我们需要写出代码来计算J( θ \theta θ) 和这些偏导数,然后把这些插入到梯度下降中,然后它就可以为我们最小化这个函数。
 法) 就是其中一些更高级的优化算法,它们需要有一种方法来计算 J( θ \theta θ),以及需要一种方法计算导数项,然后使用比梯度下降更复杂的算法来最小化代价函数。
法) 就是其中一些更高级的优化算法,它们需要有一种方法来计算 J( θ \theta θ),以及需要一种方法计算导数项,然后使用比梯度下降更复杂的算法来最小化代价函数。
多类别分类:一对多
在本节视频中,我们将谈到如何使用逻辑回归 来解决多类别分类问题,通过一个叫做"一对多" 的分类算法。
先看这样一些例子。
第一个例子:假如说你现在需要一个学习算法能自动地将邮件归类到不同的文件夹里,我们就有了这样一个分类问题:其类别有四个,分别用 = 1、 = 2、 = 3、 = 4 来代表。
第二个例子是有关药物诊断的,如果一个病人因为鼻塞来到你的诊所,他可能并没有生病,用 = 1 这个类别来代表;或者患了感冒,用 = 2 来代表;或者得了流感用 = 3来代表。
第三个例子:如果你正在做有关天气的机器学习分类问题,那么你可能想要区分哪些天是晴天、多云、雨天、或者下雪天,对上述所有的例子, 可以取一个很小的值,一个相对"谨慎"的数值,比如 1 到 3、1 到 4 或者其它数值,以上说的都是多类分类问题.
对于一个多类分类问题,我们的数据集或许看起来像这样:

我用 3 种不同的符号来代表 3 个类别,问题就是给出 3 个类型的数据集,我们如何得到一个学习算法来进行分类呢?
使用"一对余"方法。
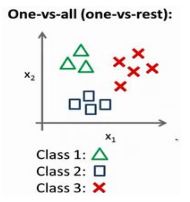
我们先从用三角形代表的类别 1 开始,实际上我们可以创建一个,新的"伪"训练集,类型 2 和类型 3 定为负类,类型 1 设定为正类,我们创建一个新的训练集,如下图所示的那样,我们要拟合出一个合适的分类器。


正则化
正则化的目的角度:正则化是为了防止过拟合
过拟合的问题
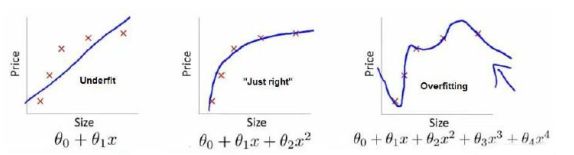
过拟合:看第一张图最右边就懂了。
我们学过的算法能够有效地解决许多问题,但是当将它们应用到某些特定的机器学习应用时,会遇到过拟合的问题,可能会导致它们效果很差。正则化的技术,它可以改善或者减少过度拟合问题。如果我们有非常多的特征,我们通过学习得到的假设可能能够非常好地适应训练集(代价函数可能几乎为 0),但是可能会不能推广到新的数据。
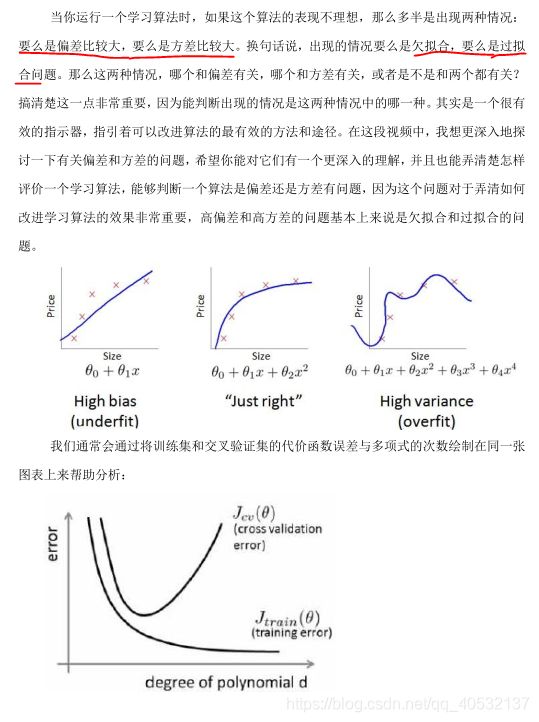
- 第一个模型是一个线性模型,欠拟合,不能很好地适应我们的训练集;
- 第三个模型是一个四次方的模型,过于强调拟合原始数据,而丢失了算法的本质:预测新数据。我们可以看
出,若给出一个新的值使之预测,它将表现的很差,是过拟合,虽然能非常好地适应我们的训练集但在新输入变量进行预测时可能会效果不好; - 中间的模型似乎最合适
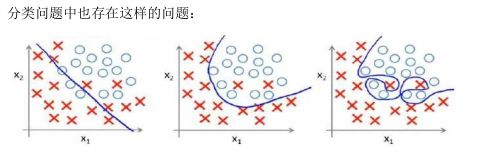
如果我们发现了过拟合问题,应该如何处理?
1.丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征,或者使用一些模型选择的算法来帮忙
2.正则化。 保留所有的特征,但是减少参数的大小。
代价函数
正则化线性回归
![]()
正则化的逻辑回归模型
下降法来优化代价函数J( θ \theta θ),接下来学习了更高级的优化算法,这些高级优化算法需要自己设计代价函数J( θ \theta θ)。


![]()

神经网络
非线性假设
无论是线性回归还是逻辑回归都有这样一个缺点,即:当特征太多时,计算的负荷会非常大。


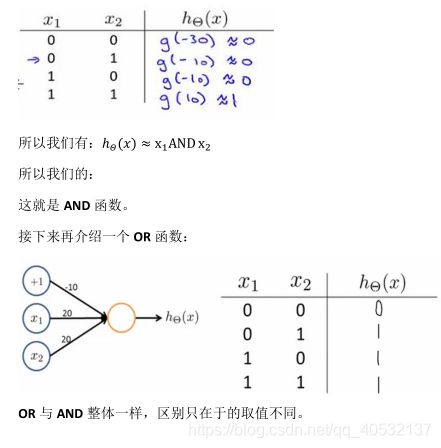
模型表示1
模型表示2
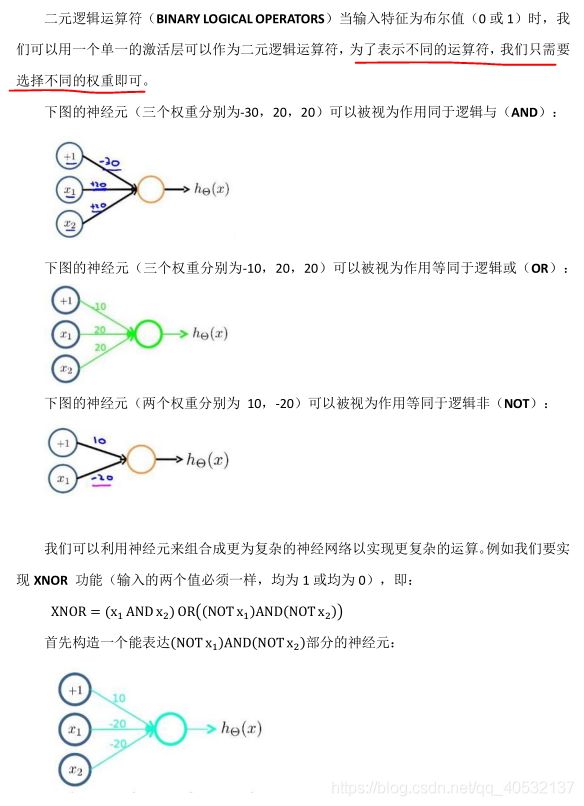
特征和直观理解 1
特征和直观理解 2
神经网络的学习
代价函数
反向传播算法
反向传播算法的直观理解
实现注意:展开参数
上节我们谈到了怎样使用反向传播算法计算代价函数的导数。在这节中,介绍一个细节的实现过程,怎样把参数从矩阵展开成向量,以便我们在高级最优化步骤中的使用需要。

梯度检验
随机初始化
任何优化算法都需要一些初始的参数。到目前为止我们都是初始所有参数为 0,这样的初始方法对于逻辑回归来说是可行的,但是对于神经网络来说是不可行的。
如果我们令所有的初始参数都为 0,这将意味着我们第二层的所有激活单元都会有相同的值。同理,如果我们初始所有的参数都为一个非 0 的数,结果也是一样的。
综合起来
应用机器学习的建议
评估一个假设
模型选择和交叉验证集
诊断偏差和方差
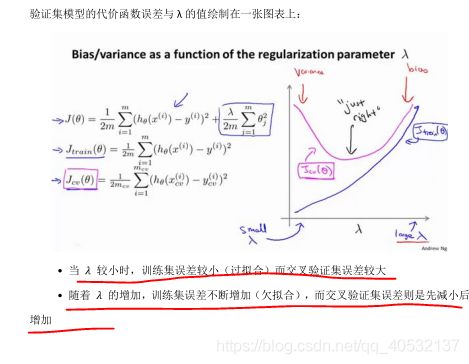
正则化和偏差/方差
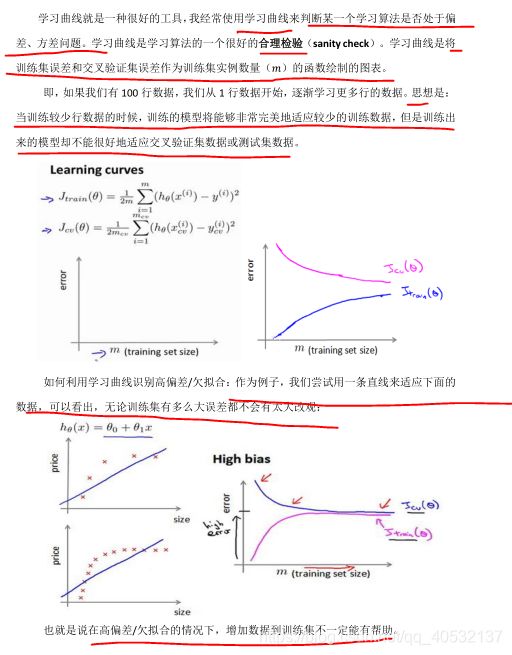
学习曲线
决定下一步做什么
机器学习系统的设计
首先要做什么
误差分析
类偏斜的误差度量
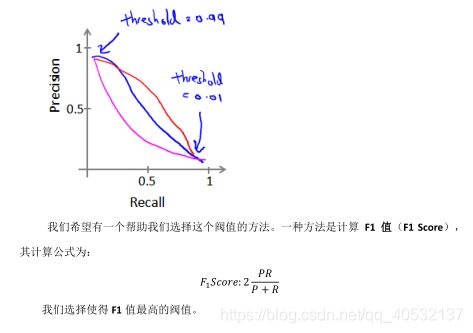
查准率和查全率之间的权衡
机器学习的数据


因为这可以证明 y可以根据特征值x被准确地预测出来。其次,我们实际上能得到一组庞大的训练集,并且在这个训练集中训练一个有很多参数的学习算法吗?如果你不能做到这两者,那么更多时候,你会得到一个性能很好的学习算法。
统计学习及监督学习概论
交叉验证
泛化能力
泛化能力是指机器学习算法对新鲜样本的适应能力。 学习的目的是学到隐含在数据背后的规律,对具有同一规律的学习集以外的数据,经过训练的网络也能给出合适的输出,该能力称为泛化能力。
感知机
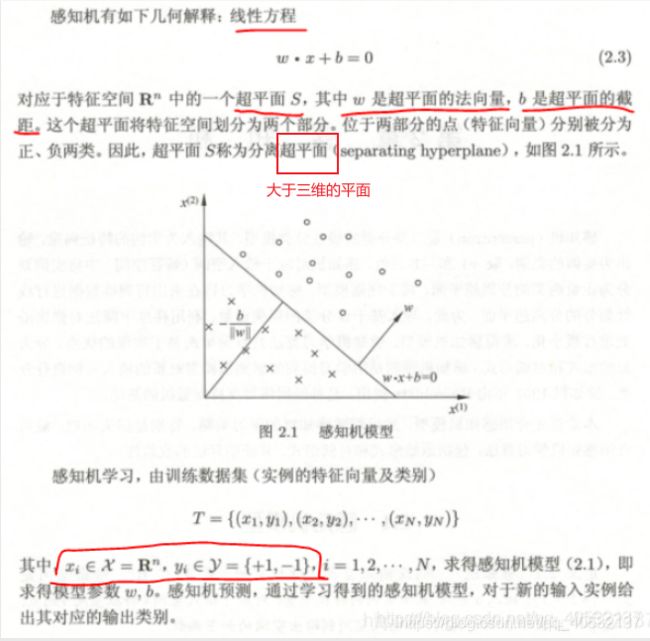
感知机模型
感知机学习策略
数据集的线性可分性
感知机学习策略
什么是范数?
感知机学习算法
感知机学习算法的原始形式

倒三角数学符号:表示对函数在各个正交方向上求导数以后再分别乘上各个方向上的单位向量;直接作用函数表示梯度,点乘函数(矢量)表示散度,叉乘函数(矢量)表旋度。

sign(x)或者Sign(x)叫做符号函数,在数学和计算机运算中,其功能是取某个数的符号(正或负):
当x>0,sign(x)=1;
当x=0,sign(x)=0;
当x<0, sign(x)=-1;

(1)(2)都是随机的;
更新w,b使用了上图的算法;
第一个是损失函数,目的为了求出损失函数最小的解;


感知机的对偶形式
对偶形式的目的是降低每次迭代的运算量,但是并不是在任何情况下都能降低运算量,而是在特征空间的维度远大于数据集大小时才起作用。




本章概要
感知机代码理解
matplotlib.pyplot使用简介
numpy 是什么?
import numpy as np
import matplotlib.pyplot as plt
p_x = np.array([[3, 3], [4, 3], [1, 1]])#创建数组
y = np.array([1, 1, -1])#这个数组相当于类别
plt.figure()
for i in range(len(p_x)):#把三个圆点画出来
if y[i] == 1:
plt.plot(p_x[i][0], p_x[i][1], 'ro')#o代表小圆圈,r=red
else:
plt.plot(p_x[i][0], p_x[i][1], 'bo')
w = np.array([1, 0])#这三个是随机取的初值
b = 0
delta = 1
for i in range(100):#计算出超平面的w和b
choice = -1
for j in range(len(p_x)):
if y[j] != np.sign(np.dot(w, p_x[0]) + b):
choice = j
break
if choice == -1:
break
w = w + delta * y[choice]*p_x[choice]
b = b + delta * y[choice]
line_x = [0, 10]
line_y = [0, 0]
for i in range(len(line_x)):#一点点点的画出了斜线
line_y[i] = (-w[0] * line_x[i]- b)/w[1]
plt.plot(line_x, line_y)
plt.savefig("picture.png")
k近邻法
1.1 k-近邻法简介
k近邻法是一种基本分类与回归方法。它的工作原理是:存在一个训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一个数据与所属分类的对应关系。
输入没有标签的新数据后,将新的数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本最相似数据(最近邻)的分类标签。一般来说,我们只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,通常k是不大于20的整数。最后,选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
举个简单的例子,我们可以使用k-近邻算法分类一个电影是爱情片还是动作片。
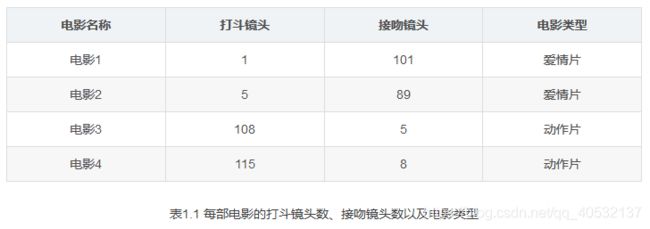
表1.1就是我们已有的训练样本集。这个数据集有两个特征,即打斗镜头数和接吻镜头数。除此之外,我们也知道每个电影的所属类型,即分类标签。用肉眼粗略地观察,接吻镜头多的,是爱情片。打斗镜头多的,是动作片。以我们多年的看片经验,这个分类还算合理。
如果现在给我一部电影,你告诉我这个电影打斗镜头数和接吻镜头数。不告诉我这个电影类型,我可以根据你给我的信息进行判断,这个电影是属于爱情片还是动作片。而k-近邻算法也可以像我们人一样做到这一点,不同的地方在于,我们的经验更"牛逼",而k-邻近算法是靠已有的数据。
比如,你告诉我这个电影打斗镜头数为2,接吻镜头数为102,我的经验会告诉你这个是爱情片,k-近邻算法也会告诉你这个是爱情片。你又告诉我另一个电影打斗镜头数为49,接吻镜头数为51,我"邪恶"的经验可能会告诉你,这有可能是个"爱情动作片",画面太美,我不敢想象。 但是k-近邻算法不会告诉你这些,因为在它的眼里,电影类型只有爱情片和动作片,它会提取样本集中特征最相似数据(最邻近)的分类标签,得到的结果可能是爱情片,也可能是动作片,但绝不会是"爱情动作片"。当然,这些取决于数据集的大小以及最近邻的判断标准等因素。
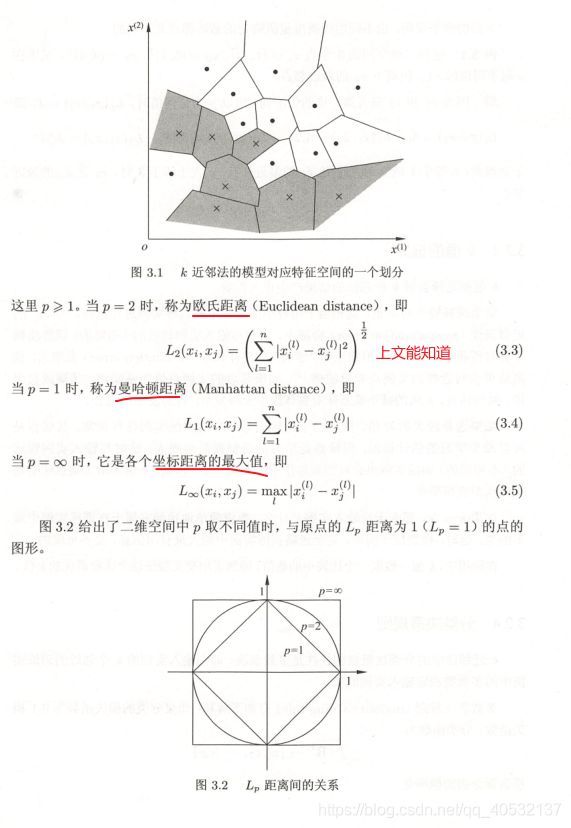
距离度量
我们已经知道k-近邻算法根据特征比较,然后提取样本集中特征最相似数据(最邻近)的分类标签。那么,如何进行比较呢?比如,我们还是以表1.1为例,怎么判断红色圆点标记的电影所属的类别呢?如图1.1所示。
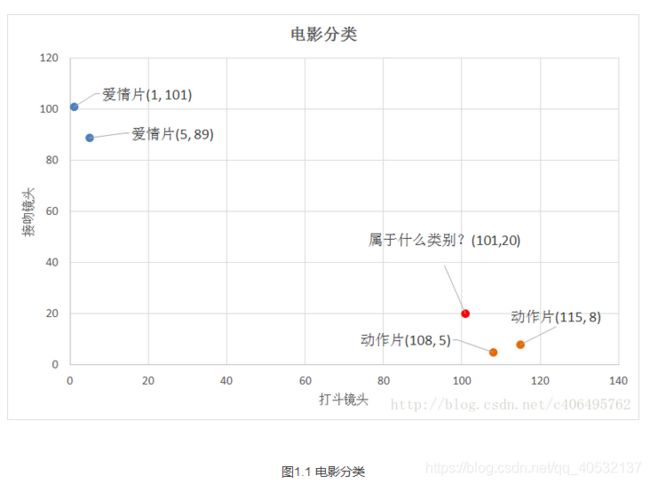
我们可以从散点图大致推断,这个红色圆点标记的电影可能属于动作片,因为距离已知的那两个动作片的圆点更近。k-近邻算法用什么方法进行判断呢?没错,就是距离度量。这个电影分类的例子有2个特征,也就是在2维实数向量空间,可以使用我们高中学过的两点距离公式计算距离,如图1.2所示。
![]()
通过计算,我们可以得到如下结果:
- (101,20)->动作片(108,5)的距离约为16.55
- (101,20)->动作片(115,8)的距离约为18.44
- (101,20)->爱情片(5,89)的距离约为118.22
- (101,20)->爱情片(1,101)的距离约为128.69
通过计算可知,红色圆点标记的电影到动作片 (108,5)的距离最近,为16.55。如果算法直接根据这个结果,判断该红色圆点标记的电影为动作片,这个算法就是最近邻算法,而非k-近邻算法。那么k-邻近算法是什么呢?
k-近邻算法步骤如下:
1.计算已知类别数据集中的点与当前点之间的距离;
2. 按照距离递增次序排序;
3.选取与当前点距离最小的k个点;
4.确定前k个点所在类别的出现频率;
5.返回前k个点所出现频率最高的类别作为当前点的预测分类。
比如,现在我这个k值取3,那么在电影例子中,按距离依次排序的三个点分别是动作片(108,5)、动作片(115,8)、爱情片(5,89)。在这三个点中,动作片出现的频率为三分之二,爱情片出现的频率为三分之一,所以该红色圆点标记的电影为动作片。这个判别过程就是k-近邻算法。
到这里,也许有人早已经发现,电影例子中的特征是2维的,这样的距离度量可以用两点距离公式计算,但是如果是更高维的呢?对,没错。我们可以用欧氏距离,如图1.5所示。我们高中所学的两点距离公式就是欧氏距离在二维空间上的公式,也就是欧氏距离的n的值为2的情况。

看到这里,有人可能会问:“分类器何种情况下会出错?”或者“答案是否总是正确的?”答案是否定的,分类器并不会得到百分百正确的结果,我们可以使用多种方法检测分类器的正确率。
此外分类器的性能也会受到多种因素的影响,如分类器设置和数据集等。不同的算法在不同数据集上的表现可能完全不同。为了测试分类器的效果,我们可以使用已知答案的数据,当然答案不能告诉分类器,检验分类器给出的结果是否符合预期结果。通过大量的测试数据,我们可以得到分类器的错误率-分类器给出错误结果的次数除以测试执行的总数。
错误率是常用的评估方法,主要用于评估分类器在某个数据集上的执行效果。完美分类器的错误率为0,最差分类器的错误率是1.0。同时,我们也不难发现,k-近邻算法没有进行数据的训练,直接使用未知的数据与已知的数据进行比较,得到结果。因此,可以说k-邻近算法不具有显式的学习过程。
k近邻算法
y = argmax f(x) 代表:y 是f(x)函式中,会产生最大输出的那个参数x。
指示函数:定义在某集合X上的函数,表示其中有哪些元素属于某一子集A。


k近邻模型

近似误差:可以理解为对现有训练集的训练误差。
估计误差:可以理解为对测试集的测试误差。
近似误差关注训练集,如果近似误差小了会出现过拟合的现象,对现有的训练集能有很好的预测,但是对未知的测试样本将会出现较大偏差的预测。模型本身不是最接近最佳模型。
估计误差关注测试集,估计误差小了说明对未知数据的预测能力好。模型本身最接近最佳模型。



k近邻法的实现:kd树
本章概要
朴素贝叶斯法
朴素贝叶斯法的学习与分类

y = argmax f(x) 代表:y 是f(x)函式中,会产生最大输出的那个参数x。
分母使用了全概率公式。


条件期望和联合分布
![]()

朴素贝叶斯法的参数估计
条件概率,指示函数,先验概率,贝叶斯定理
朴素贝斯法中学习意味着估计先验概率和后验概率,进而求出后验概率,即分类。所以要学参数估计。
N:样本的个数。
机器学习中参数估计方法最基du本的zhi就是极大似然估计。,极大似然估计结果完全依赖于给定的样本数据,它视待估参数为一个未知但固定的量,从而不考虑先验知识的影响。因此如果样本数据不能很好反映模型的情况,那么得到的参数估计结果就会有较大偏差。为了减小这个偏差,于是我们就采用贝叶斯估计方法。


这个算法用了贝叶斯定理,求出后验概率(即通过结果求原因)
因为argmax 所以不需要贝叶斯定理中的分母。

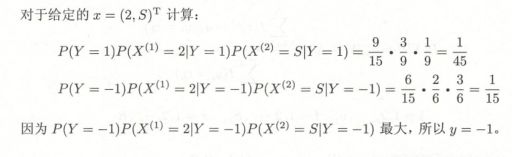
本章概要
决策树
决策树模型与学习
特征选择
决策树的生成
决策树的剪枝
CART算法
本章概要
逻辑斯谛回归与最大熵模型
逻辑斯谛回归模型
最大熵模型
模型学习的最优化算法


二值函数是指通过某种函数将值输出二值化。简单讲就是指将输入转化为仅有两种可能结果的输出
Jensen不等式
exp()函数