MATLAB实现费诺编码的计算与分析
一、实验目的
1、理解霍费诺编码的原理。
2、掌握费诺编码的方法和步骤。
3、熟悉费诺编码的效率。
4、本实验用Matlab语言编程实现费诺(Fano)编码。
二、实验环境
windows XP,MATLAB 7
三、实验原理
费诺编码算法如下:在信源符号集合中,首先将概率空间分为两个大致一样的概率集合,再将这两个概率集合进行重复分解,直到只剩下两个概率值为止。得到了一张树图,从树根开始,将编码符号1 和0 分配在同一节点的任意两分支上,这一分配过程重复直到树叶。从树根到树叶途经支路上的编码最后就构成了一组异前置码,就是费诺编码输出。
离散无记忆信源:
例如:
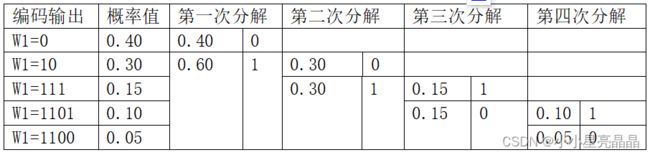
U u1 u2 u3 u4 u5
P(U) = 0.4 0.3 0.15 0.1 0.05
通过上表的对信源等格划分分解过程,从而完成对信源的费诺编码。主要分为两步,首先是码树形成过程:对信源概率进行二次分解得到编码码树。然后是码树赋值过程:在码树上分配编码码字并最终得到费诺编码。
包括:
1、码树形成过程:将信源概率按照从小到大顺序排序并建立相应的位置索引。然后按上述规则进行信源分解划分,再对二划分信源重新分解建立新的位置索引,直到分解到最后分支结束。
2、码树回溯过程:在码树上分配编码码字并最终得到费诺编码。从索引矩阵M 的首行开始前置得到编码输出。
四、实验内容
1、在给定离散无记忆信源
S s1 s2 s3 s4
P = 1/8 5/16 7/16 1/8
条件下,实现费诺编码,求最后得到的码字并算出编码效率。
2、请自己构造两个信源空间,每个空间数据不少于10个,根据费诺编码结果对比理解其相关索引指标,并进行编码效率结果对比分析验证。
五、实验过程
1、在给定离散无记忆信源条件下,实现费诺编码
费诺编码步骤为:
(1)将信源符号按其出现的概率由大到小依次排列;
(2)将依次排列的信源符号按概率值分为两大组,使两个组的概率之和近于相同,并对各组分别赋予一个二进制码元“0”和“1”;
(3)将每一大组的信源符号进一步再分成两组,使划分后的两个组的概率之和近于相同,并又分别赋予一个二进制符号“0”和“1”;
(4)如此重复,直至每个组只剩下一个信源符号为止;
(5)信源符号所对应的码字即为费诺码。
费诺编码代码如下:
function[W,L,q]=fano(P)
%1)排序
n=length(P);
x=1:n;
% 2)将信源符号分组并得到对应的码宇
for i=1:n
current_index=i;
j=1;
current_P=P;
while 1
[next_P,code_num,next_index]=compare(current_P,current_index);
current_index=next_index;
current_P=next_P;
W(i,j)=code_num;
j=j+1;
if(length(current_P)==1)
break;
end
end
l(i)=length(find(abs(W(i,:))~=0));%得到各码宇的长度
end
L=sum(P.*l);%计算平均码字长度
H=sum(P.*(-log2(P)));%计算信源熵
q=H/L; %计算编码效率
%打印输出结果
for i=1:n
B{i}=x(i);
end
[m,n]=size(W);
TEMP=blanks(m);
W=[W,TEMP',TEMP',TEMP'];
[m,n]=size(W);
W=reshape(W',1,m*n);
fprintf('信源符号出现的概率为:\n');
disp(P);
fprintf('Fano编码所得码字W:\n');
disp(B),disp(W);
fprintf('Fano编码平均码字长度L:');
disp(L);
fprintf('信源的信息熵H:');
disp(H);
fprintf('Fano编码的编码效率q:');
disp(q);
其中还使用了一个比较函数,用于信源符号的分组:
function[next_P,code_num,next_index]=compare(current_P,current_index);
n=length(current_P);
add(1)=current_P(1);
%1)求概率的依次累加和
for i=2:n
add(i)=0;
add(i)=add(i-1)+current_P(i);
end
%2)求概率和最接近的两小组
s=add(n);
for i=1:n
temp(i)=abs(s-2*add(i));
end
[c,k]=min(temp);
%3)对分组的信源赋ASCII值
if(current_index<=k)
next_index=current_index;
code_num=48;
next_P=current_P(1:k);
else
next_index=current_index-k;
code_num=49;
next_P=current_P((k+1):n);
end
在给定信源的主函数代码如下:
clc
clear
s=[1 2 3 4];
p=[1/8 5/16 7/16 1/8];%给定信源
fano(p);
2、构造两个信源空间,求它们的费诺编码
在上例1中的费诺编码代码(即fano.m)基础上,修改主程序代码如下:
clc
clear
p1=[0.08 0.12 0.05 0.20 0.15 0.06 0.17 0.01 0.09 0.07];%信源空间1
fano(p1);
p2=[0.10 0.20 0.05 0.04 0.05 0.06 0.25 0.15 0.01 0.09];%信源空间2
fano(p2);
信源空间p1=[0.08 0.12 0.05 0.20 0.15 0.06 0.17 0.01 0.09 0.07]的运行结果如下:
信源空间p2=[0.10 0.20 0.05 0.04 0.05 0.06 0.25 0.15 0.01 0.09]的运行结果如下:
比较两组信源结果可知:一个信源空间中经常出现的信源符号(即信源概率高的符号)能对应码长较短的编码字,反之,信源概率出现较低的符号的编码字对应的码长就较长。
六、实验小结
费诺编码也是一种常见的信源编码方法,它考虑了信源的统计特性,使概率大的信源符号能对应码长较短的码字,从而有效地提高了编码效率,因此,费诺码也是一种好的编码方法。
费诺编码较为适合于对分组概率相等或接近的信源编码,但不一定能使短码得到充分利用。当信源符号较多时,若有一些符号概率分布很接近,分两大组的组合方法就会有很多种,可能某种分大组的结果,会使后面小组的“概率和”相差较远,从而使平均码长增加。