密码学基础自研
密码学基础
博主一个23考研党,寒假自己复习密码学,一些笔记希望能给大家一些帮助,博主一般将一个要考试的科目知识的掌握度分为:理解知识点;会做本知识点的题目;知道本知识点会怎么出题(知道了这个知识点那里重要哪里易于混淆)。
基础术语
明文(M) :加密前你所要发送的信息。
密文(C):加密明文得到的结果。
加密密钥(K):加密明文时的一个参数。
解密密钥(K):解密密文时的一个参数。
加密算法和解密算法(E和D):加解密时所用的算法。
以上的字母都表示一个集合,例如M表示所有可能的明文组成的有限集。
密码体制分类
对称密码体制:简单来说就是发送方使用的加密密钥和接收方使用的解密密钥相同。此类体制的安全性主要取决于密钥保密性而非算法保密性。
非对称密码体制:发送方使用的加密密钥和接收方使用的解密密钥不相同。
密码攻击概述
密码分析是基于Kerckhoffs原则:攻击者知道加密算法内部机理但不知道加密密钥。
(1)唯密文攻击:攻击者有一些消息密文,这些密文都由相同加密算法加密的到,攻击者要恢复尽可能多的明文,或者能推算出加密密钥,以便采取相同的密钥解密更多密文。
(2)已知明文攻击:攻击者不仅得到一部分密文,并且知道了密文对应的明文,攻击者要用已知信息推算出加密密钥或者导出加密算法,此算法可以对同一密钥加密的任何信息加密。
(3)选择明文攻击:攻击者可以选择明文知道对应的密文,比已知明文更加有效,因为可以选择特定的明文消息进行加密,得到密钥的更多信息,攻击者要用已知信息推算出加密密钥或者导出加密算法,此算法可以对同一密钥加密的任何信息加密。
(4)选择密文攻击:可选择对应密文的明文,以此推导出加密密钥。

还有两个概念值得注意。第一, 一个加密算法是无条件安全的,如果算法产生的密文
不能给出惟一决定相应明文的足够信息。此时无论敌手截获多少密文、花费多少时间,都
不能解密密文。第二, Shannon 指出, 仅当密钥至少和明文一样长时, 才能达到无条件安
全。也就是说除了一次一密方案外, 再无其他加密方案是无条件安全的。因此,加密算法
只要满足以下两条准则之一就行:
① 破译密文的代价超过被加密信息的价值。
② 破译密文所花的时间超过信息的有用期。
满足以上两个准则的加密算法称为计算上安全的。
古典密码
古典密码是指从密码产生到近代密码之间这段时期。古典密码中很多经典的密码如凯撒密码,维吉尼亚密码等。
凯撒密码:其实就是移位密码,通过对明文里每一个消息向前移动固定个key个单位来实现加密。
先在英文字母和0~25之间形成一一对应的关系。
| A | 0 |
|---|---|
| B | 1 |
| C | 2 |
| … | … |
| Z | 25 |
然后e(x)= (x+key)mod 26 得出加密后的序列,再根据上表得到密文。
解密过程和上述流程相同,仅需要改变算法d(y)= (y-key)mod 26
仿射密码:仿射密码是移位密码的一种推广,也是需要建立对应关系。
仿射密码体制:e(x)= (k1 * x+ k2)mod 26 , gcd(k1 , 26) = 1,k1与26互素。
解密:d(y)= k1^(-1) *(y-k2)mod 26 这里就牵扯到一部分数论的知识,求逆元,常用的方法是扩展欧几里得算法。
要说扩展欧几里得算法,则要先知道欧几里得算法,在这里,我们不多做证明,只用结论,比如求156和27的最大公因数
156 = 27 * 5 + 21
27 = 21 * 1 +6
21 = 6 * 3 +3
6 = 32 + 0
故156和27最大公因数为3,而扩展欧几里得算法则是逆用,可以得出s a + t* b=gcd(a,b),中的解s,t.具体方法是将gcd(a,b)带入上式倒数第二步,然后逆运算,若a与b互素则可以得出s=a^(-1) mod b称作s为a在模b下的逆元。
例:已知一仿射密码加密密钥k1,k2分别为7,3求解密算法
这道题目其实就是求7^(-1) mod 26,首先写出求26和7的欧几里得算法步骤
26 = 7 * 3 + 5
7 = 5 * 1 + 2
5 = 2 * 2 + 1 ok,我们写到余数为一就足够了
此时,1 = 5 - 2* 2 mod26
1 = 5 - (7-5* 1)* 2 mod26
1 = 5 - (7-(26-7*3)*1)*2 mod26
然后我们在化简时要注意,7前的系数就是它的逆元 1 = 5 - 7 * 8 mod 26 而 5mod26 = -21 所以
1 = -11 * 7mod26,所以7的逆元为-11 也可以15,因为-11mod26 = 15
所以解密算法:d(y)= 15 *(y-3)mod 26
我们在计算逆元时简化后一定要形成 1 = s * a mod n的形式
维吉尼亚密码:上述的两种加密方式都是基于单表代换,也就是说字母表中的每一个字母会被加密成唯一密文,考虑到频率分析法具有很强的破解单表代换的能力,人们开始考虑使用多表代换。
频率分析法:对大量密文进行分析,通过明密文高低频率字母的对应关系来破解密钥。此种方法密文越多越容易破解。
密码体制定义:设有整数m,对任意密钥key = (k1,k2…km)
e(x1,x2…xm) = (x1+k1,x2+k2…)mod26
d(y1,y2…ym) = (y1-k1, y2-k2…)mod26这体现了分组密码的思想
一定程度上具有抵抗频率分析法的攻击。
例:m=8,密钥字为computer,明文为abcdefghig,密文是什么
首先由密钥字得k = (02,14,12,15,20,19,04,17)
密文序列是 02,15,14,18,24,24,10,24,10,23密文为cposyykykx
Hill密码:Hill密码是置换密码中非常典型的例子,置换密码不像上面几种是将英文字母写成另一个形式加密,而是通过重新排列位置来进行加密其中体现着分组——置换的思想。其中非常典型的Hill密码的加密体制为:设m为一大于等于2的整数,k为m* m的矩阵的集合,且A属于k
e(x)= A* xmod26
d(y)= A^(-1)*ymod26
x和y为一长度为m的列向量,A^(-1)为A的逆矩阵。
对称密码体制
对称密码体制包含两大类密码:流密码与分组密码,我们先来说分组密码。我们之前接触过具有分组思想的Hill密码,但它还称不上分组密码,现代密码学体系中有标准的分组密码设计准则,我们从最基础的Feistel分组密码来学习分组密码。
Feistel分组密码基本结构: Feistel分组密码基于香农提出的交替使用替换和置换的方式构造密码体制的设想构造的密码,在密码设计中,香浓提出了能够破坏对密码系统进行各种统计的分析攻击的两个基本操作,混淆和扩散。
混淆:使密文和密钥间统计关系尽可能复杂。在混淆过程中,我们让每一个密文和加密密钥之间取得得关系更加复杂
扩散:使明文和密文间统计关系尽可能复杂。在扩散过程中,我们让每一个明文信息尽可能和更多的密文相关,就是将明文的统计特性散布到密文中去,实现方式是使得明文的每一位影响密文中多位的值, 等价于说密文中每一位均受明文中多位影响。
如何实现混淆与扩散,根据我们前面学习的古典密码思想,在置换密码中我们其实已经实现了扩散,在仿射密码中我们实现了混淆。接下来我们来在Feistel分组密码体制中更加深刻认识混淆和扩散。
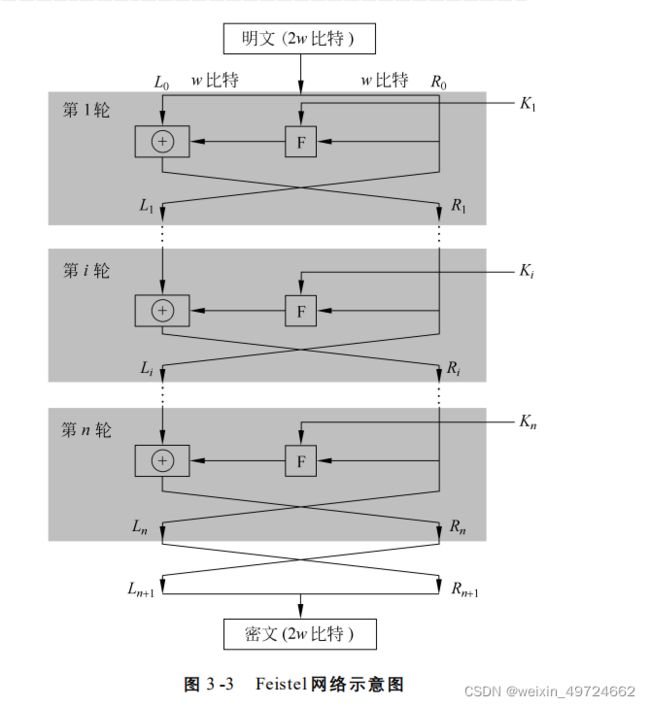
通过图片我们能初步认识Feistel分组密码体制,简要概括就是先将长为2w明文分为两个长度为w的L0和R0,R0通过F函数变换后再与L0异或,得到的结果作为下一次输入的R1,上一步的R0作为下一步的L1,首先在整个加密过程中密文长度始终不变,我们再来分析每一步的作用,分组后R0进入轮函数F中目的是做混淆操作(使密文和密钥之间统计关系变复杂),这里得到的输出再与L0进行异或目的是做扩散操作。而Ki实际上由密钥生成算法(已知初始密钥)得到每一轮加密的密钥。解密就是从下向上再返回回去。
此种加密体制安全性取决于以下:1.明文消息与密文消息分组大小(分组长度越大越安全)
2.子密钥大小,算法安全性随子密钥长度增加但效率随之降低。
3.循环次数:循环次数越多越安全随之效率越低。
4.子密钥产生算法:初始密钥给定,密钥产生算法越复杂加密越安全。
5.轮函数F:越复杂,一般来说加密越安全。
F函数的设计准则
F函数必须是非线性的,其非线性程度越强其对应的算法安全性能越高