深度学习（3）——softmax回归

前言

之前所讲的是利用线性回归来预测一个离散结果，例如波士顿房价的那个例子，当房价与房屋参数存在线性关系，那么可以在已知房屋参数的前提下利用线性回归来预测房价。
那么现在的生活中可能还有许多分类问题，给出一张照片判断是个什么类型的物品，这就需要用到今天所讲的softmax回归了。

要解决的问题

深度学习在解决一些分类问题时，有一个特别常用的数据集：Fashion-MNIST数据集，他在MNIST数据集上作了大幅改进，它里面包含了6000张训练图片以及10000张测试图片，每张图片都有一个分类结果，总共有10个类别。接下来我们将用softmax来试试分类效果如何。
传统线性回归的模型是：Y=Xw+b，通过小批量随机梯度下降来使得权重值w以及误差值b趋近于最合理的值。
softmax回归模型也是通过小批量梯度下降来获得最合理的权重值与误差值，线性回归以房屋属性作为一种变量，来获取它对应的权重；在图片分类问题中，将图片的像素点作为最小单位变量，这些像素点将对应着权重；然后这些图片将最终被分为10个类，每个类对每张图片像素点的权重值是不一样的；最终通过Y=Xw+b的模型得到每张图片在十个类别下的概率分布，至于为什么会变成概率分布，我们下文再讲。
这里举个极简的例子：
一张图片只有4像素：a,b,c,d
假设图片最终会被分成三类，每张图片中的每个像素点将对应着一个权重，那么4个像素就有4个权重，那么这三类就会有3套不同的权重组合。
第一类图片给予每个像素的权重是x1，y1，z1，w1；
第二类图片给予每个像素的权重是x2，y2，z2，w2；
第三类图片给予每个像素的权重是x3，y3，z3，w3
一类图片的权重作为一列，那么形成4*3的矩阵，
那么当像素点的数值点乘每类图片的权重值时，我们就形成了A_1*4 ·A_4*3 =A_1*3

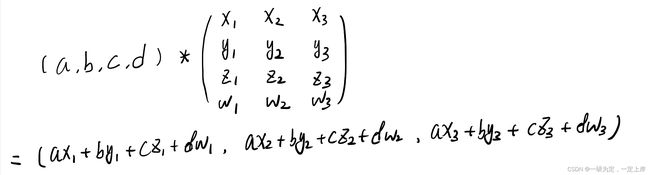
矩阵点乘出来的这三个数据分别对应着三个类别，最大数字对应的类别就是softmax预测出来的结果。
简单讲述了一下大致思路，下面将详细讲解

数据集的读取

要用的包

%matplotlib inline
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l

d2l.use_svg_display()

在torchvision里面内置了我们要用的Mnist数据集

读取数据集

def load_data_fashion_mnist(batch_size, resize=None):  #@save
    """下载Fashion-MNIST数据集，然后将其加载到内存中"""
    # 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式
    # 并除以255使得所有像素的数值均在0到1之间
    trans = [transforms.ToTensor()]
    #默认图像是28*28的尺寸，resize变量可以更改尺寸大小
    if resize:
        trans.insert(0, transforms.Resize(resize))
    trans = transforms.Compose(trans)
    #读取训练与测试数据
    mnist_train = torchvision.datasets.FashionMNIST(
        root="../data", train=True, transform=trans, download=True)
    mnist_test = torchvision.datasets.FashionMNIST(
        root="../data", train=False, transform=trans, download=True)
    #返回batch_size个训练和测试数据，shuffle变量表示是否要打乱下标，上一个blog有讲过
    #打乱下标可以让每一次的迭代选取的顺序不一样，训练需要，测试一般不需要
    #get_dataloader_workers表示需要几个进程来读取数据
    return (data.DataLoader(mnist_train, batch_size, shuffle=True,
                            num_workers=get_dataloader_workers()),
            data.DataLoader(mnist_test, batch_size, shuffle=False,
                            num_workers=get_dataloader_workers()))

基于softmax回归实现图片分类问题

要用的包

import torch
from IPython import display
from d2l import torch as d2l

之前数据集读取的那些方法全部集成在d2l这个包里了

获得图片数据

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

分别获得每批256个的训练样本以及测试样本

初始化模型参数

回忆一下我们要用的模型，依旧是y=Xw+b，我们这里要初始化的就是w和b

# 因为每张图片都是28*28的格式，我们把这个二维图形降维成一个长度为784个像素的数组，此时我们忽略降维带来的误差
num_inputs = 784
#有十个图形类别，就会有十组长度为784的权重组
num_outputs = 10
#w默认随机取正态分布中的值，w的矩阵规格为784*10，b初始赋0，长度为10
W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

定义softmax操作

这步是用来干嘛的呢，我们在之前介绍softmax回归大致思路的时候讲到了我们最终是根据Xw+b后得到的概率，取概率最大值所代表的图像类别最后的预测结果。
那么我们一定会有疑问，X是一堆0至1的数据代表每个像素的颜色深浅，w是一堆-1到1的正态分布数字，b初始为0暂且不谈，就看Xw有正有负怎么可能被作为概率，势必要做处理，那么softmax就是来做这件事的。

实现softmax由三个步骤组成：

1（变正）、对每个项求幂（使用exp）；
2、对每一行求和（小批量中每个样本是一行），得到每个样本的规范化常数；
3、(形成概率）将每一行除以其规范化常数，确保结果的和为1。
在查看代码之前，我们回顾一下这个表达式：

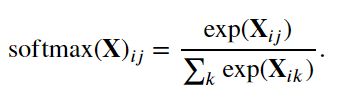
分母或规范化常数，有时也称为配分函数（其对数称为对数-配分函数）。 该名称来自统计物理学中一个模拟粒子群分布的方程。

接下来，看代码：
三行代码对应步骤123

def softmax(X):
    X_exp = torch.exp(X)
    partition = X_exp.sum(1, keepdim=True) #torch.sum（）中的第一个参数：0代表列求和，1代表行求和
    return X_exp / partition  # 这里应用了广播机制

找个例子看一下效果：

# X是一个2行5列的正态分布矩阵
X = torch.normal(0, 1, (2, 5))
print(X)
#softmax后的结果
X_prob = softmax(X)
X_prob, X_prob.sum(1)

结果：

原始数据：tensor([[-0.9751,  0.0864,  1.1050,  0.6132, -0.9473],
        [ 1.8591,  0.8396, -1.1432, -0.2780,  0.7191]])
softmax后：(tensor([[0.0561, 0.1622, 0.4492, 0.2747, 0.0577],
         [0.5410, 0.1952, 0.0269, 0.0638, 0.1730]]),
每行和： tensor([1., 1.]))

定义模型

这步就是将Xw+b后的结果softmax处理。

def net(X):
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + 

损失函数

在机器学习中损失函数算是比较重要的一环，在后续学习中慢慢体会.
本章介绍一个经典损失函数：交叉熵损失函数，用于分类问题比较多。
交叉熵采用真实标签的预测概率的负对数似然，公式如下：

具体推导过程参考李沐大神的课件：

代码展示：

def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y])

其中y_hat（）举个例子便于理解：

y = torch.tensor([0, 2, 1]) #真实结果
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5], [0, 1, 0]]) #预测结果
#其中[0.1, 0.3, 0.6]代表该图像是类别012的概率分别是0.1，0.3，0.6
y_hat[[0, 1, 2], y]#获得每张图片预测正确的概率，第一张图真实是类别0，那么他的预测概率就是0.1

tensor([0.1000, 0.5000, 1.0000])

那么我们的交叉熵损失函数的代码就好理解了

cross_entropy(y_hat, y)

tensor([2.3026, 0.6931, -0.0000])

类似上一章节，我们将损失函数作小批量随机梯度下降，下文再展开

模型精度测试

获取预测正确数量

这个代码逻辑就是一张图片的预测概率最大值所对应的图片类别等于这张图片的真实图片类别，那就正确

def accuracy(y_hat, y):  #@save
    """计算预测正确的数量"""
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.type(y.dtype) == y
    return float(cmp.type(y.dtype).sum())
accuracy(y_hat, y) / len(y) #用这个可以计算准确率了
0.66

计算模型精度

这个代码可以计算任意数据在任何一个模型下的精度

def evaluate_accuracy(net, data_iter):  #@save
    """计算在指定数据集上模型的精度"""
    if isinstance(net, torch.nn.Module): #使用神经网络模型的情形 
        net.eval()  # 将模型设置为评估模式，不计算梯度
    metric = Accumulator(2)  # 正确预测数、预测总数
    with torch.no_grad():
        for X, y in data_iter:
        	#向metric增加每一批次数据预测正确的数量以及每批的数据量
            metric.add(accuracy(net(X), y), y.numel()) 
    return metric[0] / metric[1] #返回这个模型的准确率

Accumulator函数代码：

class Accumulator:  #@save
    """在n个变量上累加"""
    def __init__(self, n):
        self.data = [0.0] * n

    def add(self, *args):
        self.data = [a + float(b) for a, b in zip(self.data, args)]

    def reset(self):
        self.data = [0.0] * len(self.data)

    def __getitem__(self, idx):
        return self.data[idx]

使用随机权重的任意模型精度大约在10%

训练

一次迭代

一次迭代周期，也就是把6000个训练数据都过一遍的结果

def train_epoch_ch3(net, train_iter, loss, updater):  #@save
    """训练模型一个迭代周期"""
    # 将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train() #要计算梯度
    # 训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)
    for X, y in train_iter: 
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad()
            l.mean().backward()
            updater.step()
        else:
            # 使用定制的优化器和损失函数
            # 我们这里会用到小批量随机梯度下降
            l.sum().backward()
            updater(X.shape[0])
        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回训练损失和训练精度
    return metric[0] / metric[2], metric[1] / metric[2]

可视化

这个函数用于可视化展示通过多次迭代后图片分类的准确性变化

class Animator:  #@save
    """在动画中绘制数据"""
    def __init__(self, xlabel=None, ylabel=None, legend=None, xlim=None,
                 ylim=None, xscale='linear', yscale='linear',
                 fmts=('-', 'm--', 'g-.', 'r:'), nrows=1, ncols=1,
                 figsize=(3.5, 2.5)):
        # 增量地绘制多条线
        if legend is None:
            legend = []
        d2l.use_svg_display()
        self.fig, self.axes = d2l.plt.subplots(nrows, ncols, figsize=figsize)
        if nrows * ncols == 1:
            self.axes = [self.axes, ]
        # 使用lambda函数捕获参数
        self.config_axes = lambda: d2l.set_axes(
            self.axes[0], xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
        self.X, self.Y, self.fmts = None, None, fmts

    def add(self, x, y):
        # 向图表中添加多个数据点
        if not hasattr(y, "__len__"):
            y = [y]
        n = len(y)
        if not hasattr(x, "__len__"):
            x = [x] * n
        if not self.X:
            self.X = [[] for _ in range(n)]
        if not self.Y:
            self.Y = [[] for _ in range(n)]
        for i, (a, b) in enumerate(zip(x, y)):
            if a is not None and b is not None:
                self.X[i].append(a)
                self.Y[i].append(b)
        self.axes[0].cla()
        for x, y, fmt in zip(self.X, self.Y, self.fmts):
            self.axes[0].plot(x, y, fmt)
        self.config_axes()
        display.display(self.fig)
        display.clear_output(wait=True)

最终训练函数

def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  #@save
    """训练模型"""
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                        legend=['train loss', 'train acc', 'test acc'])
    for epoch in range(num_epochs):
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
        test_acc = evaluate_accuracy(net, test_iter)
        animator.add(epoch + 1, train_metrics + (test_acc,))
    train_loss, train_acc = train_metrics
    #assert 断言 false 报错
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc

本问题使用小批量随机梯度下降

lr = 0.1

def updater(batch_size):
    return d2l.sgd([W, b], lr, batch_size)

测试

num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

预测

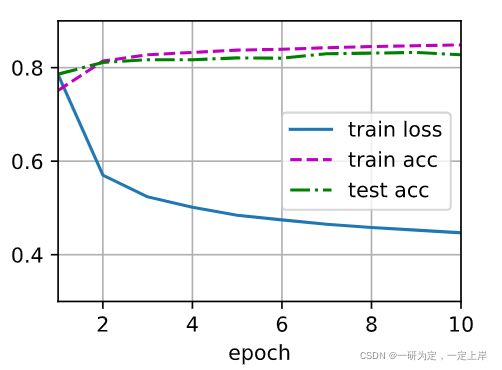
完成了上述的十次迭代后，看到准确率已经达到了9成左右，因此可以来做实际的预测工作

def predict_ch3(net, test_iter, n=6):  #@save
    """预测标签（定义见第3章）"""
    for X, y in test_iter:
        break
    #trues记录真实的图片分类，并转换成字符串
    trues = d2l.get_fashion_mnist_labels(y)
    #preds记录每张图片在十个分类中最高概率的图片分类名称
    preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
    titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
    #可视化展示结果
    d2l.show_images(
        X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])

predict_ch3(net, test_iter)

小结

像这种图片分类问题，他其实是有一定规律的，像鞋子，他一定会在某些像素点上有比较深的体现，像这样的类似分类问题，我们可以用softmax来求解。
本文详细的讲了softmax的实现，当然pytorch这个强大的库里当然内置了softmax方法，我们直接调用就好了，我们现在去刨开详细讲是为了给深度学习打下坚实基础。另外作为一名研究生，我们不仅仅要学会去使用这些方法，我们更要能够去优化这些方法，使得它更优，这样也方便我们发论文了。好，下一章介绍使用内置方法快速实现softmax！
欢迎批评与指正！