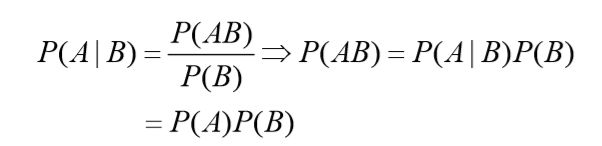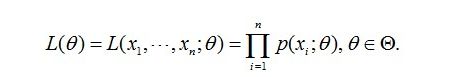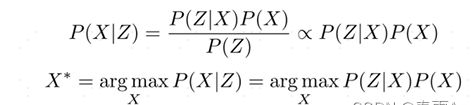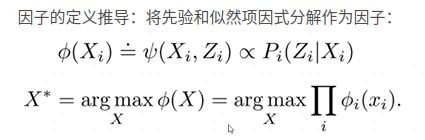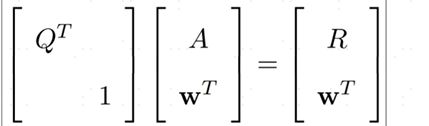似然与贝叶斯
一、理解
1、基础
独立:
全概率:P(A)=P(B1)P(A|B1)+P(B2)P(A|B2)+...+P(Bn)P(A|Bn)
2、贝叶斯公式:
1、公式
2、理解
我们在日常生活中常常是观察到某种现象,然后去反推造成这种现象的各种原因的概率。简单来说,就是由果推因
最终求得的条件概率P(Bi|A),就是在观察到结果事件A已经发生的情况下,推断结果事件A是由原因Bi造成的概率的大小,以支撑我们后续的判断
3、似然
概率是根据条件推测结果,而似然则是根据结果反推条件
假定已知某个参数B时,推测事件A会发生的概率写作
通过贝叶斯公式,可以得出
现在我们反过来:事件A发生已经了,请通过似然函数
,估计参数B的可能性
3.1、 似然函数举例:已知样本X,求参数θ
在七月在线那么多男学员中,我一抽就抽到这100个男生,而不是其他人,那说明在整个学校中,这100个人(的身高)出现的概率最大啊,这个概率就是上面这个似然函数L(θ),怎么做到的呢?换言之,怎样的θ能让L(θ)最大?
3.2、极大似然即最大可能
3.3、EM算法中的隐变量
一般的用Y表示观测到的随机变量的数据,Z表示隐随机变量的数据(因为我们观测不到结果是从哪个概率分布中得出的,所以将这个叫做隐变量)。于是Y和Z连在一起被称为完全数据,仅Y一个被称为不完全数据。
这时有没有发现EM算法面临的问题主要就是:有个隐变量数据Z。而如果Z已知的话,那问题就可用极大似然估计求解了。 于是乎,怎么把Z变成已知的?
EM算法的思想就是:
1给θ自主规定个初值(既然我不知道想实现“两个碟子平均分配锅里的菜”的话每个碟子需要有多少菜,那我就先估计个值);
2根据给定观测数据和当前的参数θ,求未观测数据z的条件概率分布的期望(在上一步中,已经根据手感将菜倒进了两个碟子,然后这一步根据“两个碟子里都有菜”和“当前两个碟子都有多少菜”来判断自己倒菜的手感);
3上一步中z已经求出来了,于是根据极大似然估计求最优的θ’(手感已经有了,那就根据手感判断下盘子里应该有多少菜,然后把菜匀匀);
4因为第二步和第三步的结果可能不是最优的,所以重复第二步和第三步,直到收敛(重复多次匀匀的过程,直到两个碟子中菜的量大致一样)。
二、公式推导
- EM算法的目标函数
从(2)式到(3)式,神奇的地方有两点:
当我们在求(2)式的极大值时,(2)式不太好计算,我们便想(2)式大于某个方便计算的下界(3)式,而我们尽可能让下界(3)式最大化,直到(3)式的计算结果等于(2)式,便也就间接求得了(2)式的极大值;
Jensen不等式,促进神奇发生的Jensen不等式到底是什么来历呢?
如果f是凸函数,X是随机变量,那么:E[f(X)]>=f(E[X]),通俗的说法是函数的期望大于等于期望的函数。
特别地,如果f是严格凸函数,当且仅当P(X = EX) = 1,即X是常量时,上式取等号,即E[f(X)] = f(EX)。凹函数则 反过来
当然,当f是(严格)凹函数当且仅当-f是(严格)凸函数,不等号方向反向,也就是
- EM算法的流程及证明
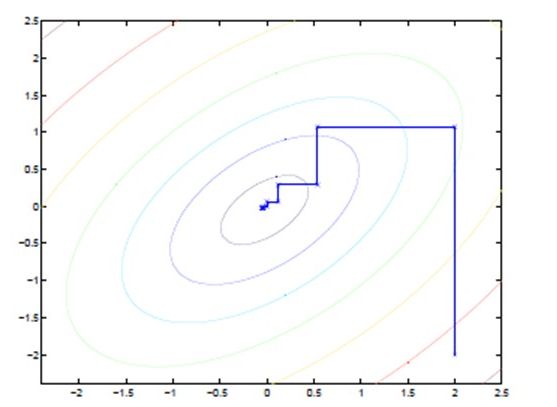
EM算法另一种理解
图中的直线式迭代优化的路径,可以看到每一步都会向最优值前进一步,而且前进路线是平行于坐标轴的,因为每一步只优化一个变量。
这犹如在x-y坐标系中找一个曲线的极值,然而曲线函数不能直接求导,因此什么梯度下降方法就不适用了。但固定一个变量后,另外一个可以通过求导得到,因此可以使用坐标上升法,一次固定一个变量,对另外的求极值,最后逐步逼近极值。
对应到EM上,就是:E步:固定θ,优化Q;M步:固定Q,优化θ;交替将极值推向最大。
三、slam 后端, 知道观测变量, 推出状态变量
后验概率问题MAP
通过上面的定义将MAP问题转换成求解一个最优的状态,使得似然概率和先验概率的乘积最大化
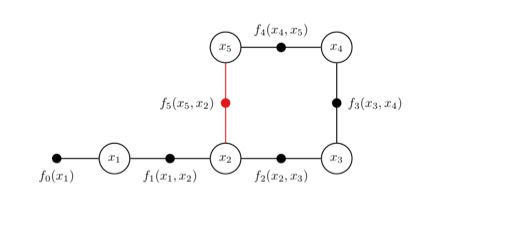
将上述乘积形式的每一项表示成因子,将状态变量表示成节点,观测量表示成边,就转化成了下面的因子图
其中红色的部分表示观测因子,绿色为里程计因子,紫色为先验因子。那我们要解决的问题是什么呢,就是寻找一个最优的X,使得这些因子图的乘积最大化
因子图中每个因子的定义:在因子图中通常每个因子都是通过指数函数的形式来定义的,这是因为我们得到的观测量是有不确定性的,而且现实中这种不确定性通常服从高斯分布
其中f(x)表示的是误差函数,当误差越小的时候,其指数函数越大,其定义如下图所示
贝叶斯网络可以解决已知状态变量来推出观测变量的问题,但是事实是我们通常可以得到观测变量,想要推出状态变量,所以我们推出了因子图,并且结合贝叶斯定理,将问题描述成一个最大后验概率问题。最终得到目标函数
贝叶斯网络可以解决已知状态变量来推出观测变量的问题,但是事实是我们通常可以得到观测变量,想要推出状态变量,所以我们推出了因子图,并且结合贝叶斯定理,将问题描述成一个最大后验概率问题。最终得到目标函数
取对数,转化为非线性最小二乘问题
1、非线性最小二乘问题求解
牛顿法
泰勒展开,将非线性转化为线性
现在的问题就转化成了如何求解这个线性最小二乘问题,对于一个线性最小二乘问题是由比较成熟的方法来得到线性最小而成问题的最优解,比较常见的方法为Normal equation:
对于Normal equation问题可以通过Cholesky分解来求解:
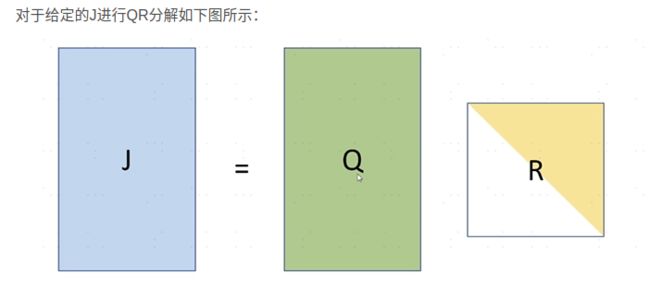
也可以通过QR分解来求解
2、例子
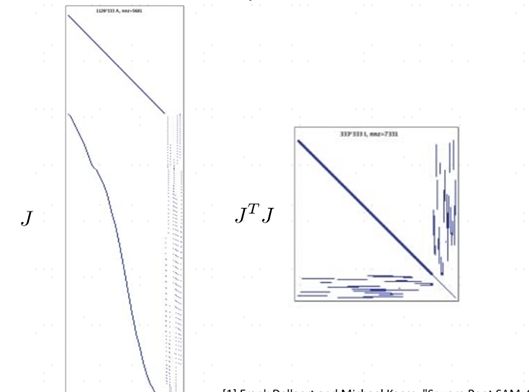
上图中的雅可比矩阵的每一行对应一个因子,右边的矩阵是一个信息矩阵,在现实中生成的因子图所获得的雅可比矩阵是稀疏矩阵,这是一个很好的性质,非常有利于线性系统的求解
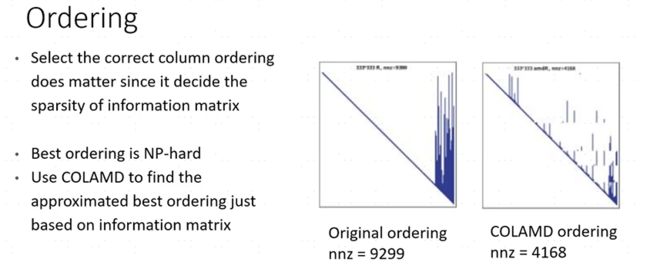
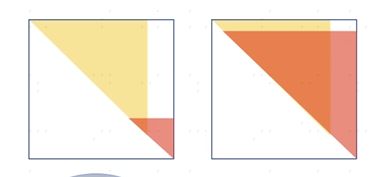
但是这个矩阵的稀疏性和变量的order有关,order不一样的话,矩阵的稀疏性体现也不一样,会出现下图所示的情况
对信息矩阵进行重排序来维持其好的稀疏性,目前较为成熟的算法为COLAMD。通过上面的描述我们知道了对于一个确定的因子图如何求解。但是常见的问题(比如SLAM问题)生成的因子图是增量的,并且在机器人运行的过程中,因子图只是又很小一部分的改变,如果我们从头对因子图进行分解来求解的话,不利于系统的实时性,那么如何解决这个问题呢?下面介绍论文isam中是怎么做的。.
3、isam1增量QR分解
论文:
其求解办法是通过givens rotation可以将R变成一个新的上三角矩阵
但是随着因子的增加,也会带来一个问题,就是如果我新加的因子只影响上一时刻的因子的时候,这个矩阵依然是有很好的稀疏性,但是如果新加入的因子是回环,那么givens rotation讲影响之前的所有节点,使R矩阵变得稠密,如下图所示
这时候就体现出了isam1的问题,在经过以一定的时间后就需要对元素进行重新排序,将稠密矩阵变得稀疏:
4、isam2
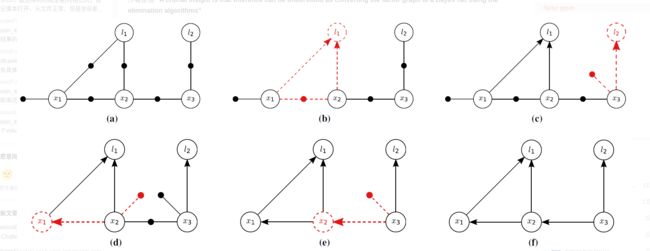
变量消去过程
上图中 (a) 是原始的 factor graph,(b) (c) (d) (e) (f) 分别对应消去变量 l1l1 l2l2 x1x1 x2x2 x3x3 时的 factor graph
简单来说就是图优化是一次获取所有位姿信息进行优化,因子图优化是逐帧获取逐帧优化,实时且只优化关联帧的位姿信息。
gra 就是图的两个点连线边的约束, 里面是相对的位姿变化量
initPose 是位姿点
然后定义graph 是整个图, 当前状态,包含小部分约束的
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
using namespace gtsam;
int main()
{
// 向量保存好模拟的位姿和测量,到时候一个个往isam2里填加
std::vector< BetweenFactor > gra;
std::vector< Pose2 > initPose;
noiseModel::Diagonal::shared_ptr model = noiseModel::Diagonal::Sigmas(Vector3(0.2, 0.2, 0.1));
gra.push_back(BetweenFactor(1, 2, Pose2(2, 0, 0 ), model));
gra.push_back(BetweenFactor(2, 3, Pose2(2, 0, M_PI_2), model));
gra.push_back(BetweenFactor(3, 4, Pose2(2, 0, M_PI_2), model));
gra.push_back(BetweenFactor(4, 5, Pose2(2, 0, M_PI_2), model));
gra.push_back(BetweenFactor(5, 2, Pose2(2, 0, M_PI_2), model));
initPose.push_back(Pose2(0.5, 0.0, 0.2 ));
initPose.push_back( Pose2(2.3, 0.1, -0.2 ));
initPose.push_back( Pose2(4.1, 0.1, M_PI_2));
initPose.push_back( Pose2(4.0, 2.0, M_PI ));
initPose.push_back( Pose2(2.1, 2.1, -M_PI_2));
ISAM2Params parameters;
parameters.relinearizeThreshold = 0.01;
parameters.relinearizeSkip = 1;
ISAM2 isam(parameters);
// 注意isam2的graph里只添加isam2更新状态以后新测量到的约束
NonlinearFactorGraph graph;
Values initialEstimate;
// the first pose don't need to update
for( int i =0; i<5 ;i++)
{
// Add an initial guess for the current pose
initialEstimate.insert(i+1, initPose[i]);
if(i == 0)
{
// Add a prior on the first pose, setting it to the origin
// A prior factor consists of a mean and a noise model (covariance matrix)
noiseModel::Diagonal::shared_ptr priorNoise = noiseModel::Diagonal::Sigmas(Vector3(0.3, 0.3, 0.1));
graph.push_back(PriorFactor(1, Pose2(0, 0, 0), priorNoise));
}else
{
graph.push_back(gra[i-1]); // ie: when i = 1 , robot at pos2, there is a edge gra[0] between pos1 and pos2
if(i == 4)
{
graph.push_back(gra[4]); // when robot at pos5, there two edge, one is pos4 ->pos5, another is pos5->pos2 (grad[4])
}
isam.update(graph, initialEstimate);
isam.update();
Values currentEstimate = isam.calculateEstimate();
cout << "****************************************************" << endl;
cout << "Frame " << i << ": " << endl;
currentEstimate.print("Current estimate: ");
// Clear the factor graph and values for the next iteration
// 特别重要,update以后,清空原来的约束。已经加入到isam2的那些会用bayes tree保管,你不用操心了。
graph.resize(0);
initialEstimate.clear();
}
}
return 0;
}
效果逐帧更新, 每帧是一个位姿,比如是x3
Lego-LOAM 因子图优化
//系列头文件
#include
#include
#include
#include
#include
#include
#include
#include
#include
//系列声明与初始化
using namespace gtsam;
NonlinearFactorGraph gtSAMgraph;
Values initialEstimate;
Values optimizedEstimate;
ISAM2 *isam;
Values isamCurrentEstimate;
noiseModel::Diagonal::shared_ptr priorNoise;
noiseModel::Diagonal::shared_ptr odometryNoise;
noiseModel::Diagonal::shared_ptr constraintNoise;
//初始化
ISAM2Params parameters;
parameters.relinearizeThreshold = 0.01;
parameters.relinearizeSkip = 1;
isam = new ISAM2(parameters);
gtsam::Vector Vector6(6);
Vector6 << 1e-6, 1e-6, 1e-6, 1e-8, 1e-8, 1e-6;
priorNoise = noiseModel::Diagonal::Variances(Vector6);
odometryNoise = noiseModel::Diagonal::Variances(Vector6);
.......
//在回环检测线程中,当找到闭环,就添加回环因子
gtsam::Pose3 poseFrom = Pose3(Rot3::RzRyRx(roll, pitch, yaw), Point3(x, y, z));
gtsam::Pose3 poseTo = pclPointTogtsamPose3(cloudKeyPoses6D->points[closestHistoryFrameID]);
gtsam::Vector Vector6(6);
float noiseScore = icp.getFitnessScore();
Vector6 << noiseScore, noiseScore, noiseScore, noiseScore, noiseScore, noiseScore;
constraintNoise = noiseModel::Diagonal::Variances(Vector6);
/* add constraints*/
std::lock_guard lock(mtx);
gtSAMgraph.add(BetweenFactor(latestFrameIDLoopCloure, closestHistoryFrameID, poseFrom.between(poseTo), constraintNoise));
isam->update(gtSAMgraph);
isam->update();
gtSAMgraph.resize(0);
.......
//在保存关键帧和因子中,先是添加固定先验因子
if (cloudKeyPoses3D->points.empty())
{
gtSAMgraph.add(PriorFactor(0, Pose3(Rot3::RzRyRx(transformTobeMapped[2], transformTobeMapped[0], transformTobeMapped[1]),Point3(transformTobeMapped[5], transformTobeMapped[3], transformTobeMapped[4])), priorNoise));
initialEstimate.insert(0, Pose3(Rot3::RzRyRx(transformTobeMapped[2], transformTobeMapped[0], transformTobeMapped[1]),Point3(transformTobeMapped[5], transformTobeMapped[3], transformTobeMapped[4])));
for (int i = 0; i < 6; ++i)
transformLast[i] = transformTobeMapped[i];
}
.......
//随后添加位姿间的二元因子
else
{
gtsam::Pose3 poseFrom = Pose3(Rot3::RzRyRx(transformLast[2], transformLast[0], transformLast[1]),Point3(transformLast[5], transformLast[3], transformLast[4]));
gtsam::Pose3 poseTo = Pose3(Rot3::RzRyRx(transformAftMapped[2], transformAftMapped[0], transformAftMapped[1]),Point3(transformAftMapped[5], transformAftMapped[3], transformAftMapped[4]));
gtSAMgraph.add(BetweenFactor(cloudKeyPoses3D->points.size()-1, cloudKeyPoses3D->points.size(), poseFrom.between(poseTo), odometryNoise));
initialEstimate.insert(cloudKeyPoses3D->points.size(), Pose3(Rot3::RzRyRx(transformAftMapped[2], transformAftMapped[0], transformAftMapped[1]),Point3(transformAftMapped[5], transformAftMapped[3], transformAftMapped[4])));
}
//更新isam和计算位姿
/*** update iSAM*/
isam->update(gtSAMgraph, initialEstimate);
isam->update();
gtSAMgraph.resize(0);
initialEstimate.clear();
/** save key poses*/
PointType thisPose3D;
PointTypePose thisPose6D;
Pose3 latestEstimate;
isamCurrentEstimate = isam->calculateEstimate();//计算出最终矫正后结果存放的地方
//访问最终矫正后的位姿
int numPoses = isamCurrentEstimate.size();
for (int i = 0; i < numPoses; ++i)
{
cloudKeyPoses3D->points[i].x = isamCurrentEstimate.at(i).translation().y();
cloudKeyPoses3D->points[i].y = isamCurrentEstimate.at(i).translation().z();
cloudKeyPoses3D->points[i].z = isamCurrentEstimate.at(i).translation().x();
cloudKeyPoses6D->points[i].x = cloudKeyPoses3D->points[i].x;
cloudKeyPoses6D->points[i].y = cloudKeyPoses3D->points[i].y;
cloudKeyPoses6D->points[i].z = cloudKeyPoses3D->points[i].z;
cloudKeyPoses6D->points[i].roll = isamCurrentEstimate.at(i).rotation().pitch();
cloudKeyPoses6D->points[i].pitch = isamCurrentEstimate.at(i).rotation().yaw();
cloudKeyPoses6D->points[i].yaw = isamCurrentEstimate.at(i).rotation().roll();
} 代码
https://github.com/borglab/gtsam
https://github.com/dongjing3309/gtsam-examples
参考
https://blog.csdn.net/unlimitedai/article/details/108500895?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522167375198716782428698882%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=167375198716782428698882&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_ecpm_v1~pc_rank_34-7-108500895-null-null.142^v71^pc_new_rank,201^v4^add_ask&utm_term=iSAM2