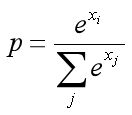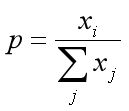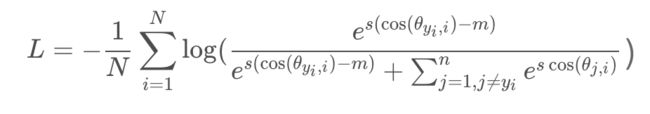度量学习（Metric learning）—— 基于分类损失函数（softmax、交叉熵、cosface、arcface）

概述

 

    首先，我们把loss归为两类：一类是本篇讲述的基于softmax的，一类是基于pair对的（如对比损失、三元损失等）。

    基于pair对的，参考我的另一篇博客： https://blog.csdn.net/u012863603/article/details/119246720

    基于softmax的改进主要有如下（有的loss拥有不同的名字）：softmax、center loss、range loss、Modified softmax、NormFace、large margin、 SphereFace （ angular softmax、A-Softmax ）、CosFace（AM Softmax两个团队撞车）、ArcFace（insightFace），其实基本上主要就是 针对特征和分类的权值向量做归一化以及不同方式的引入large margin，他们的区别就是一个不断集成的过程，发展至今，常用的是softmax，人脸等特征模型好用的CosFace、ArcFace。因此，本文主要讲这两个（当这个系列几乎到达瓶颈时，过多的去记名词和对应的改动历史，个人感觉意义不大），其余的建议参考： https://zhuanlan.zhihu.com/p/34404607

    

softmax

    在了解其他的模型的前提是先了解softmax，如上所述，其他均为softmax的改进，关于softmax这里需要解决几点常见的疑惑（之前我的疑惑和目前我的理解）：

    *softmax是什么

    *softmax 和 损失函数的关系是什么（交叉熵损失为例）

    *softmax 和 分类器什么关系

    

1、softmax 是什么

     首先，softmax 的作用是把 一个序列，变成概率。假设输入的向量为是 ，softmax的公式如下： 

    

     他能够保证：

    1）所有的值都是 [0, 1] 之间的（因为概率必须是 [0, 1]）

    2）所有的值加起来等于 1

    然后我们看一下直接求概率的结果，如下公式（我们这里称之为hardmax）

    

    Softmax 直接求解存在数值稳定的问题， 因为要算指数，只要你的输入稍微大一点，比如，[1000, 2000, 3000],  分母上就是 ， 很明显，在计算上一定会溢出。 其中一种解决方法就是使用 LogSoftmax  （然后再求  exp ）。 数值稳定性比 softmax 好一些。 可以看到， LogSoftmax 省了一个指数计算，省了一个除法，数值上相对稳定一些。

 

2、  softmax 和 损失函数的关系是什么（交叉熵损失为例）

    cross entropy 是用来衡量两个概率分布之间的距离的，假设现在有一个样本集中两个概率分布p,q，其中p为真实分布，对于离散变量，H(p,q)称之为交叉熵， 如下：

    

    softmax能把一切转换成概率分布，如（0.1，0.2，0.3，0.4）；对于多分类而言，如果采用one-hot 编码，那么label便也成了一个概率分布，如（0，0，0，1），那么自然二者自然可以结合在一起使用。

    而且通过上面讲到的softmax的述职稳定性的问题，似乎softmax和交叉熵就成了天设的一对，即使softmax数值计算更稳定，又节省了交叉熵的冗余log计算。  并且在反向求导中也变得异常简洁（求导不是本文重点，不再赘述，因为现在的训练框架支持自动求导，不需要自己实现反传过程）。

3、softmax 和分类器什么关系

    前面讲到softmax配合交叉熵构成了softmax 交叉熵损失，并且可以嵌入计算提高效率。以one hot编码，softmax的输入向量长度需要等同于类别的个数，因此需要一个全连接层将网络的特征向量映射为一个长度为类别数的向量，这个有区别于现代使用GAP（全局平均池化）替代多层FC的操作。如下图，可以认为从512维到10000维的映射全连接层为分类器，训练时接 softmax+交叉熵，测试时接softmax的到置信度（或者不接，直接取最大值）。

    

    

    对应公式如下，m代表样本数，W代表最后一层全连接的参数，b代表偏置项，x代表特征向量：

    

    我们来看用pytorch 怎么简单的实现（仅仅为了理解，pytorch本身已经实现了）

        

class Linear(nn.Module):
    def __init__(self):
        super(Linear, self).__init__()
        self.weight = nn.Parameter(torch.Tensor(2, 10))  # (input,output)
        nn.init.xavier_uniform_(self.weight)

    def forward(self, x, label):
        out = x.mm(self.weight) # 分类器的全连接层
        loss = F.cross_entropy(out, label) # 合并了softmax 和 交叉熵
        return out, loss

4、softmax存在的问题。

   hard的max和soft的max到底有什么区别呢？看几个例子

    

    如上表， 相同输入向量情况，soft max比hard max更容易达到终极目标one-hot形式，或者说，softmax降低了训练难度，使得多分类问题更容易收敛。 Softmax鼓励真实目标类别输出比其他类别要大，但并不要求大很多（如下图左） 。 Softmax Loss训练CNN，MNIST上10分类的2维特征映射可视化如下（从左到右： 二维化的特征中分布类分界线， 二维化的特征中特征的欧式距离实例， 二维化的特征中 特征归一化对应圆弧、最后一个FC的权重归一化对应该类的竖线 ）：

    

   L2距离越小，向量相似度越高。而L2距离在二维和三维空间上可以直观的理解为两个点的距离，如上右图黄色虚线代表的就是两个红色箭头指示的两个空间点（二维向量也就是特征）的距离。而分类器的最后那个全连接层对应到每个类的权重也可以理解为空间中的点（对于上面的2为mnist，时间原因，我没有写源码画出具体位置，可以猜猜大概为每个类簇的中心位置），那么softmax的输入其实就是图上的特征乘以对应的权重（忽略偏置项，直观上也就是每个特征点和对应权重的距离）。那么说对于一个固定类别（训练和真实场景一样，如mnist都是10分类）的场景来说，使用softmax， 训练的深度特征，会把整个超空间或者超球，按照分类个数进行划分，保证类别是 可分的 ， 这一点对多分类任务如MNIST和ImageNet非常合适，因为测试类别必定在训练类别中 （而且我自己认为，训练难度低会使得 优点可能更多：收敛快、一定程度上更不容易过拟合 ）。

    但是我们看到上面的场景的局限： 测试类别必定在训练类别中。 这一点非常不适合人脸识别任务，因为训练集的1W人数，相对测试集整个世界70亿人类来说，非常微不足道，而我们不可能拿到所有人的训练样本，更过分的是，一般我们还要求训练集和测试集不重叠。但是 Softmax并 不要求类内紧凑和类间分离，并且无法用通过排除类中心（分类器最后一层对应类目的权重）外去度量，比如L2距离（余弦距离同理）， 可能同类的特征向量距离（黄色）比不同类的特征向量距离（绿色）更大。

     所以需要改造Softmax，除了保证可分性外，还要做到特征向量类内尽可能紧凑，类间尽可能分离，以适用于度量的场景（测试类别不在训练类别中，如人脸）。 对比损失和三元组损失需要精心地构建图像对和三元组，耗时并且构建的训练对的好坏直接影响识别性能。

    

二、CosFace、ArcFace

1、 CosFace

    如上面的sortmax，cosface主要是将权重w和向量x进行了归一化，并乘以一个缩放系数，吸收（忽略）偏置项，增加margin。最后的损失如下：

    重点就是s和m超参数的设置，虽然官方给了两个公式，但是本质上并不能很精确的指导这两个参数的设置，尤其在类别数远大于嵌入特征的维度的case（却是人脸等嘴常见的场景，官方的实验结果是s=64，m=0.35时最好），不同的m的影响。以下是不同m的影响。

    

    

    具体实现比较简单，参考后面讲到的arcface。

2、 ArcFace

     在CosFace的基础上，ArcFace，将惩罚项由cosine函数外移到了函数内，在训练稳定的同时更进一步地提升了人脸识别网络的辨别能力。公式如下：

    

    具体实现上，在进行特征x和权重W标准化之后，它们之间的相乘等价于cosine距离cos ⁡ ( θ ) 。对其使用arc-cosine方程来计算特征和权重之间的角度θ ，然后添加一个额外的角度上的加的惩罚项m得到θ + m ，接着对其使用cosine函数得到cos ⁡ ( θ + m )，在之后进行re-scale（即按照CosFace中的方式得到s* cos ⁡ ( θ + m ) ），最后送入softmax损失函数中。

    伪代码如下：

    

开源代码如下（pytorch）

class ArcMarginProduct(nn.Module):
    r"""Implement of large margin arc distance: :
        Args:
            in_features: size of each input sample
            out_features: size of each output sample
            s: norm of input feature
            m: margin
            cos(theta + m)
        """
    def __init__(self, in_features, out_features, s=30.0, m=0.50, easy_margin=False):
        super(ArcMarginProduct, self).__init__()
        self.in_features = in_features #输入特征维度，一般是512
        self.out_features = out_features #输出维度，是类别数目
        self.s = s #re-scale
        self.m = m #角度惩罚项
        self.weight = Parameter(torch.FloatTensor(out_features, in_features)) #权重矩阵
        nn.init.xavier_uniform_(self.weight) #权重矩阵初始化

        self.easy_margin = easy_margin
        self.cos_m = math.cos(m)
        self.sin_m = math.sin(m)
        self.th = math.cos(math.pi - m)
        self.mm = math.sin(math.pi - m) * m

    def forward(self, input, label):
        # --------------------------- cos(theta) & phi(theta) ---------------------------
        # 对应伪代码中的1、2、3行：输入x标准化、输入W标准化和它们之间进行FC层得到cos(theta)
        cosine = F.linear(F.normalize(input), F.normalize(self.weight))
        # 计算sin(theta)
        sine = torch.sqrt((1.0 - torch.pow(cosine, 2)).clamp(0, 1))
        # 对应伪代码中的5、6行：计算cos(theta+m) = cos(theta)cos(m) - sin(theta)sin(m)
        phi = cosine * self.cos_m - sine * self.sin_m
        if self.easy_margin:
            phi = torch.where(cosine > 0, phi, cosine)
        else:
            # 当cos(theta)>cos(pi-m)时，phi=cos(theta)-sin(pi-m)*m
            phi = torch.where(cosine > self.th, phi, cosine - self.mm)
        # --------------------------- convert label to one-hot ---------------------------
        # 对应伪代码中的7行：对label形式进行转换，假设batch为2、有3类的话，即将label从[1,2]转换成[[0,1,0],[0,0,1]]
        one_hot = torch.zeros(cosine.size(), device='cuda')
        one_hot.scatter_(1, label.view(-1, 1).long(), 1)
        # 对应伪代码中的8行：计算公式(6)
        # -------------torch.where(out_i = {x_i if condition_i else y_i) -------------
        output = (one_hot * phi) + ((1.0 - one_hot) * cosine)  # you can use torch.where if your torch.__version__ is 0.4
        # 对应伪代码中的9行，进行re-scale
        output *= self.s

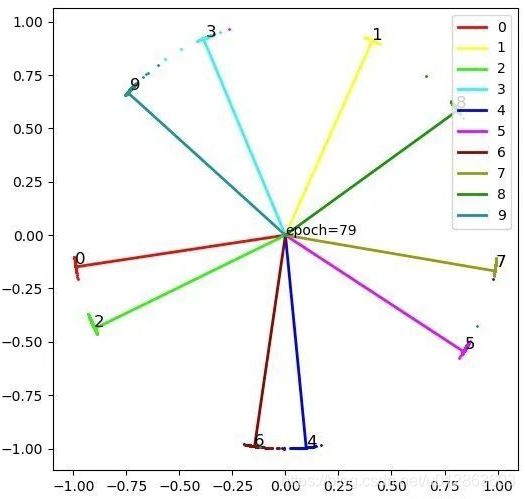
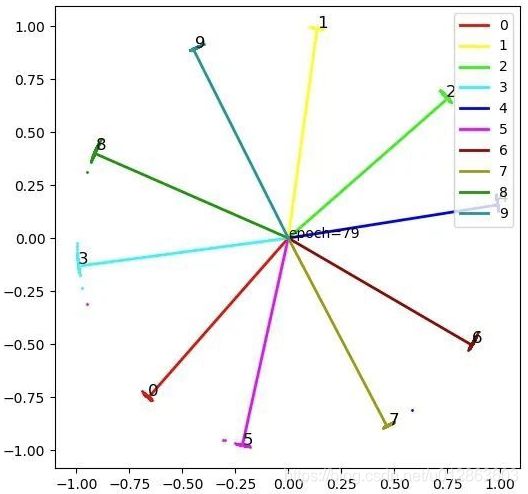
        return output

    对比softmax，arcface的特征和归一化分布如下（ ArcSoftmax需要更久的训练，这个收敛还不够充分. ）：

    

3、归一化、scale、margin的意义

     从最新方法来看，权值W和特征f(或 x )归一化已经成为了标配，而且都给归一化特征乘以尺度因子s进行放大，目前 主流都采用固定尺度因子s的方法，并且都加上了margin。

    1）归一化的重要性

    * 权值和特征归一化使得CNN更加集中在优化夹角上（可以使用余弦距离度量），得到的深度人脸 特征更加分离（训练难度增大，原因见下面的成固定尺度因子）；

    *特征向量都固定映射到半径为1的超球上，便于理解和优化；

    * 特征归一化后，人脸识别计算特征向量相似度， L2距离和cos距离意义等价，计算量也相同 ，我们再也不用纠结到底用L2距离还会用cos距离。

    2） 乘固定尺度因子

   

    *归一化会压缩特征表达的空间，造成无法收敛；

    *乘尺度因子s。直观解释：相当于将超球的半径放大到s ， 超球变大，特征表达的空间也更大 （简单理解：半径越大球的表面积越大）。理论解释如下： 仅特征归一化时，输出  {x1, x2, x3, x4}   等价于{s * cosθ, x2, x3, x4 }  ，理想情况下，优后 θ  是0，x2=x3=x4都输出0，此时激活值为{1, 0, 0, 0}，指数函数非线性放大后输出为{e, 1, 1, 1}，归一化后置信度是{47.54%, 17.49%, 17.49%, 17.49%}，远远达不到收敛的要求，所以 仅归一化是不能训练的。归一化后乘尺度因子s，这里以s=60为例，输出 {x1, x2, x3, x4}   等价于  {60* cosθ, x2, x3, x4 }  ，理想情况下，优后 θ  是0，x2=x3=x4都输出0，此时激活值为{60, 0, 0, 0}，指数函数非线性放大后输出为{exp(60), 1, 1, 1}，归一化后置信度是{100%, 0%, 0%, 0%}，完全可以达到收敛要求。所以 特征归一化必须乘尺度因子。

    其实这就是著名的normface，对应的公式和可视化如下：

    

    3）large margin

   

        其实通过归一化+乘固定尺度因子，一方面可以使用余弦距离，一方面先增加难度（归一化），再缓和难度（乘尺度因子），其实特征已经比较好，如上图，实际性能也确实是加margin有提升，但是并没有很多。下面来说明原因。

    为什么有提升。我们仍然以四分类，已经归一化且乘尺度因子的情况讨论（其余情况原理类似）：输出{x1, x2, x3, x4}  等价于{s * cosθ, x2, x3, x4}  。原始在输出x = {5, 1, 1, 1}时就接近收敛，训练停止，此时改用large margin softmax，第一列的 cosθ 强制变成cos(mθ) （即SphereFace）、 cosθ-m（即cosface）或 cos(θ+m)（即arcface），会使输出减小，其他列保持不变，此时输出可能变成了x = {4, 1, 1, 1}，网络又可以继续训练了，也就是增加训练难度，使训练得到的特征映射更好。不同loss的曲线对比，下图来自ArcFace，所有loss都是单调递减的。对比Softmax的 cosθ 曲线，乘性margin的SphereFace对应cos(mθ) 曲线下降最多，训练难度剧增，退火技术也难以收敛，反观加性margin的CosineFace和ArcFace下降较少，训练难度稍微增加，所以更容易收敛。    

        为什么提升不多（large margin 到底优化了什么）。 large margin优化的核心——夹角 θ   是权值W和特征f之间的夹角，也就是类内夹角约束，目标是让同一类的所有特征向量都拉向该类别的权值向量， 并不是不同类别之间的夹角（所以切勿鲁莽的把训练时的m当做测试时的阈值） 。因此充其量是又增加了训练难度。loss函数也完全没有涉及不同类别特征向量之间的夹角约束。 具体来看  W * f = | W | * | f | * cos θ ，考虑W和f都是归一化的，训练目标从 cosθ  变成cos(4θ)  、  cosθ  -0.35 或  cos(θ+0.5) ，都减小了输出激活值，如果要达到目标置信度100%，就需要优化出比Softmax更小的夹角 θ  ，也就是说 large margin的优化目标是让权值向量W和特征向量f之间的夹角更小 。

参考链接：

1、softmax cross-entropy关系; https://www.zhihu.com/question/294679135

2、人脸识别loss 上：  https://zhuanlan.zhihu.com/p/34404607

3、人脸识别loss 下：  https://zhuanlan.zhihu.com/p/34436551

4、 https://blog.csdn.net/qq_42732229/article/details/108349970

5、 https://zhuanlan.zhihu.com/p/35027284

6、 https://zhuanlan.zhihu.com/p/76541084

7、人脸识别函数特征可视化； https://cloud.tencent.com/developer/article/1750658

8、 https://zhuanlan.zhihu.com/p/35027284

9、 https://blog.csdn.net/AManFromEarth/article/details/107013578

10、 https://zhuanlan.zhihu.com/p/60747096