第二十二章：求解素数的N种方法

 求解素数的N种方法

一、质数和合数

质数：

质数又称**素数**。指在一个大于 1的自然数中，除了 1和此整数自身外，不能被其他自然数整除的数。换句话说，只有两个正因数（1和自己）的自然数即为质数。

最小的素数是 2， 它也是唯一的**偶素数**。

从小到大的素数依次排列为∶ 2，3，5，7，11，13，17……

合数：

比 1大但不是素数的数称为合数（0 和1 既非素数也非合数）

最小的合数是 4。

从小到大的合数依次排列为∶4，6，8，9，10，12，14……

特别注意：

判断质数跟合数的时候，一定要注意一些特殊值，例如0和1以及可能出现负数

二、最大公约数和最小公倍数

最大公约数也称为最大公因数、最大公因子，指两个或多个整数共有约数中最大的一个约数。

例如∶求 12、16 的最大公约数

12的约数∶ 1、2、3、4、6、12

16的约数∶1、2、4、8

12、16的公约数∶ 1、2、4

其中最大的一个是 4，因此 12 与16 的最大公约数是4

辗转相除法

又名欧几里德算法，是求最大公约数的一种方法。

具体做法∶对于给定的两个数 m 和 n，若除数 n 不为 0，将 m除以 n 的余数和除数 n 构成新的一对数，继续上面的除法，直到除数n 等于 0，则这时的被除数 m 就是原来两个数的最大公约数。

最小公倍数

两个或多个整数公有的倍数叫做它们的公倍数，其中除 0 以外最小的一个公倍数就叫做这几个整数的最小公倍数。

例如∶求 6、8的最小公倍数

6的倍数∶ 6、12、18、24、30、……

8的倍数∶8、16、24、32、40、……

6、8的公倍数∶ 24、48、……

其中最小的一个是 24，因此 6与8的最小公倍数是 24

总结∶各数相乘，再除以它们的最大公约数即可得到最小公倍数。

例题1：编程求两个数的最大公约数

解题思路：调用自定义函数求两个自然数的最大公约数，完整代码如下

#include 
using namespace std;
int get_gcd(int m,int n)
{
    int r;
    while(n!=0)
    {
        r=m%n;
        m=n;
        n=r;
    }
    return m;
 } 
int main()
{
    int m,n;
    cin>>m>>n;
    cout<

Copy

例题2：编程求两个数的最小公倍数

解题思路：最小公倍数=每个数相乘，再除以它们的最大公约数。调用自定义函数求两个自然数的最小公倍数，完整代码如下

#include 
using namespace std;
int get_gcd(int m,int n)
{
    int r;
    while(n!=0)
    {
        r=m%n;
        m=n;
        n=r;
    }
    return m;
} 
int lcm(int m,int n)
{
    return m*n/get_gcd(m,n);
}
int main()
{
    int m,n;
    cin>>m>>n;
    cout<

Copy

注意事项：__gcd()函数在正式比赛中可能被禁用，因此尽量手写一个gcd函数。

三、互质数

两个或多个整数的公因数只有 1 的非零自然数。

例：12 与 17 是互质数；12 与 3 不是互质数

互质数特性：（1）最大公约数为 1；（2）最小公倍数为其乘积。

如何用 C++程序来判断两个数是否为互质数？

思路：判断最大公因数是否为 1。

四、质因数分解

概念：把一个合数分解成若干个质因数的乘积的形式，即求质因数的过程叫做质因数分解。

24=2*12=2*2*6=2*2*2*3

30=2*15=2*3*5


Copy

例题1：质因数分解（主题库1890）

已知正整数 n 是两个不同的质数的乘积，试求出较大的那个质数。

输入格式 ：输入只有一行，包含一个正整数 n。

输出格式：输出只有一行，包含一个正整数 p，即较大的那个质数。

样例输入：

21

Copy

样例输出：

7

Copy

数据范围/约定

时间空间限制：1s, 256MB.

对于 60%的数据，6 ≤ n ≤ 10006≤n≤1000。

对于 100%的数据，6 ≤ n ≤ 2*10^96≤n≤2∗109。

解题思路：

#include 
using namespace std;
int main()
{
    int n,i;
    cin>>n;
    for(i=2;i<=n-1;i++)
    {
        if(n%i==0)
        {
            cout<

Copy

例题2：分解质因数（主题库1101）

分解质因数是小学数学中常见的问题，现在给定一个正整数N，请你编程序对N分解质因数，并将分解式输出来。

输入输出格式 ：

输入：只有一个正整数N（N<=32767）。

输出：只有一行，就是N分解成质因子的连乘积的式子，并且要求按因子从小到大从左到右的格式输出。

样例输入：

24

Copy

样例输出：

24=2*2*2*3

Copy

解题思路：

#include
using namespace std;
int main()
{
    int n,i;
    cin>>n;
    cout<

Copy

例题3：寻找质因数（主题库1117）

给出N个数字，试求质因数最大的数字。

输入格式：第一行，一个整数N，表示数字个数。 接下来N行，每行一个整数A_i，表示给出的数字。

输出格式：一个整数，表示质因数最大的数字。

样例输入：

4
36
38
40
42

Copy

样例输出：

38

Copy

时间及空间限制

1s, 256MB.

提示：

N < = 5000 , A_i < = 20000 举例 38和12 38=19*2 12=2*3*3 38最大的是19 12最大的是3 所以本数据要输出38

解题思路：

#include
using namespace std;
int main()
{
    int k,n,j,i,max=0,ma=0,r,t;
    cin>>k;
    for(i=1;i<=k;i++)
    {
        cin>>n;
        t=n;
        for(j=2;j<=n;j++)
        {
            if(n%j==0)
            {
                if(j>max) max=j;
                n=n/j;
                j=1;
            }
        }
        if(max>ma)
        {
            ma=max;
            r=t;
        }
    }
    cout<

Copy

求解素数的N种方法

素数即质数，类似于这种类型的题型无论是在各区区赛还是历年的市赛中都经常出现，下面我们就一起通过一道经典的例题来看看如何利用素数筛求解此类问题。

问题背景

素数（又称质数），指在大于1的自然数中，除了1和它本身以外，不能被其他其它自然数整除的数。与之相对应的是合数，合数除了1和它本身以外还可以被其他自然数整除。（ 1既不是质数也不是合数 ）。

问题描述

求出 m\sim nm∼n 中的素数的个数。(题目链接)

方法一、试除法

思考一：如何判断 i 是否为质数？

基于定义，用区间 [2,i-1][2,i−1] 中的每一个数对 ii 进行试探，若区间中存在可以整除 ii 的数，则 ii 为合数。反之为质数。

C++ 代码

// 判断一个数字 i 是否是素数，是则输出"yes"，否则输出"no"
int main()
{
    int i;
    cin >> i;
    for(int j = 2; j < i; j++)
    {
        if(i % j == 0)
        {
            cout << "no";
            return 0;
        }
    }
    cout << "yes";
    return 0;
}

Copy

写成函数如下：

// 判断一个整数 i 是不是素数，是则返回 true，否则返回 false
bool is_prime(int i){
    if(i < 2)
        return false;
    for(int j = 2; j < i; j++)
        if(i % j == 0)
            return false;
    return true;
}

Copy

思考二、上述代码能否优化？

假设 aa 和 bb 都能被 ii 整除，且 a*b = i，a \leq ba∗b=i，a≤b ，那么 必然有 a\leq \sqrt ia≤i​ 。换句话说，我们没有必要对大于 \sqrt ii​ 的数进行试探( \sqrt ii​ 即 sqrt(i))，故以上方法可以优化如下代码：

// 判断一个整数 i 是不是素数，是则返回 true，否则返回 false
bool is_prime(int i){
    if(i < 2)
        return false;
    for(int j = 2; j <= sqrt(i); j++)
        if(i % j == 0)
            return false;
    return true;
}
// j<=sqrt(i) 也就是 j*j < i，因此，上面第 5 行也可以写成
// for(int j = 2; j * j <= i; j++)
// 两种写法是等价的

Copy

思考三、时间复杂度？

第一个代码是最朴素的代码，当一个数 nn 是素数时，它需要从 22 到 n-1n−1 每个数都判断一遍，才能判断出它是不是素数，因此，该代码的时间复杂度是 O(n)O(n) 的。

经过优化之后，只需要判断到 sqrt(n)sqrt(n) ，因此，优化后的时间复杂度是 O(\sqrt n)O(n​) 的。

如果只是判断一个数是不是素数的话，试除法的时间复杂度还不算高。但是，在“求出 m\sim nm∼n 中的素数个数” 这个问题中，因为最多要对 nn 个数进行判断素数，所以，这个问题的时间复杂度就要在 O(\sqrt n)O(n​) 的基础上再乘以 nn ，达到 O(n \sqrt n)O(nn​) 。当 nn 达到 200 万时，代码将有超时的风险。

下面引入更高效的判断素数的方法——筛法。

方法二、埃氏筛法（素数筛）

思想

首先定义一个数组（初始全为 0 ），用来标记每个数字是不是素数（用 0 表示这个数是素数，用 1 表示它不是素数）。初始所有数字是不是素数并不清楚，因此，假设所有数都是素数。但是 0 和 1 肯定不是素数，因此标记为 1，2 肯定是素数，标记为 0。然后可以开始筛选素数了。

埃氏筛法的核心思想取决于这样的一个逻辑： 如果后面的数能整除当前的数，那么就表示后面的数有其他因数，那就一定不是素数。把它标记为非素数即可。 素数没有其他因数，因此，不会被标记为非素数。

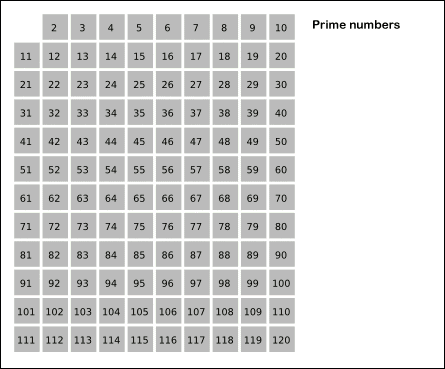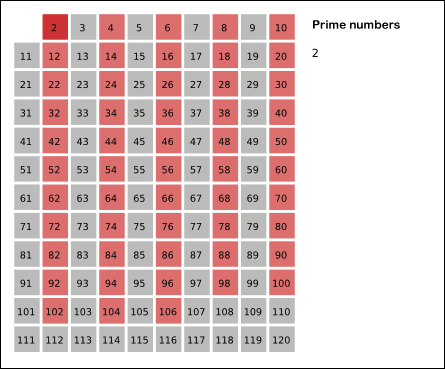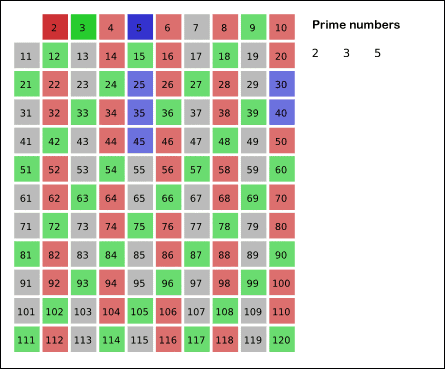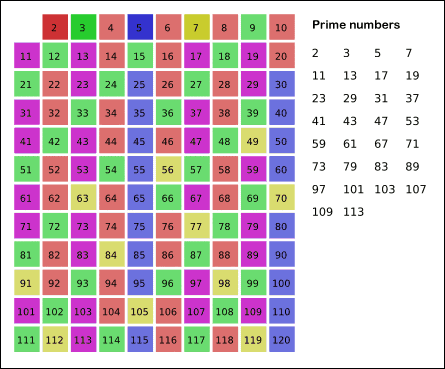
基于以上思想，埃氏筛法在处理时会先去掉 2 的倍数，再去掉 3 的倍数，再去掉 4 的倍数，……依此类推，直到最大数小于最后一个标出的素数的平方，那么剩下的序列中所有的数都是素数。

代码

const int N = 100000;   // N 的大小取决于问题中 n 的范围
bool a[N];   // 标记数组  a[i] = 0(false):素数，a[i]=1(true): 非素数
// 标记数组也可以用 int 来定义，但占用内存是 bool 的 4 倍
// 因此 bool 能开的数组范围更大，更推荐使用 bool 定义标记数组  

// 埃氏筛法 函数执行完后 a[] 数组即为筛出的素数结果 a[i]=false 表示 i 是素数
void prime()
{
    a[0]=a[1]=true;         // 0 和 1 不是素数
    for(int i = 2; i <= n; i++)
    {
        if(a[i] == false)   // i 是素数
        {
            for(int j = i+i; j <= n; j += i)
                a[j] = true;
        }
    }
}

Copy

我们发现上面的做法会有很多重复标记的情况，例如 6 被 2 和 3 标记了两次，15 被 3 和 5 标记了两次。实际上，小于 i^2i2 的 ii 的倍数在扫描更小的数的时候就已经被标记过了。所以，对于每一个质数 ii 只需要标记大于 i^2i2 的倍数即可。故最终优化的埃氏筛法如下：

const int N = 10000;
bool a[N];

void prime()
{
    a[0]=a[1]=true; 
    for(int i = 2; i <= N; i++)
    {
        if(a[i] == false)
        {
            for(int j = i*i; j <= N; j += i)  // i+i 改为 i*i，其余同上。这里注意如果N>=50000，要全部改成long long，想想为什么？
                a[j] = true;
        }
    }
}

Copy

注意重点：将i+i改成了i*i，试着说说这样做的好处。

附上一张埃氏筛法图解：

时间复杂度

埃氏筛法的时间复杂度为 O(n\log \log n)O(nloglogn) ，其中还是存在一些重复标记的情况，但是它的时间复杂度已经足够低了，当 n=10^9n=109 时，\log \log nloglogn 也只是接近 4 左右。对于竞赛中的素数判断问题，使用埃氏筛也足够了。

不过作为一个问题的解法来说，埃氏筛还不是最优的，下面引入更优的线性时间复杂度的筛法——欧拉筛法。

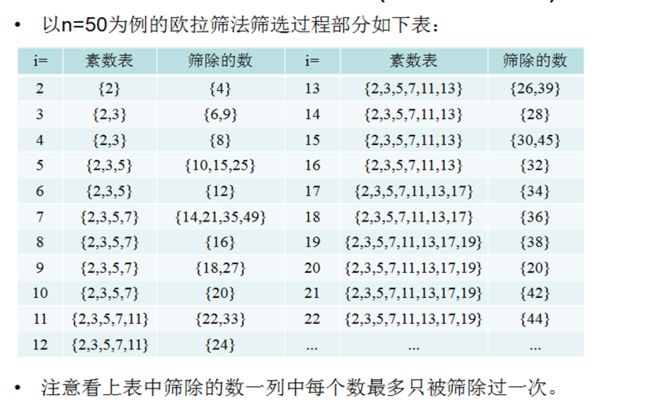
方法三、欧式筛法

思想

核心原理：对于每个合数，都只由它最小的质因子筛掉。

欧式筛的思想比较难以理解，因此，我们先看代码，再解释。

代码

const int N =10001000;
bool a[N];     // 初始默认全是素数
int prime[N];
// 欧式筛法
void prime()
{
    a[0]=a[1]=true;      // 这条语句可以不写，只是为了定义的严谨性而加的
    int h=0;
    for(int i = 2; i <= N; i++)
    {
        if(a[i] == false)
            prime[h++] = i;  
        for(int j=0; j

Copy

关于原理的解释

假定 prime[] 数组中存放着已经确定的素数，很显然，里面的素数是从小到大存放的。然后我们要逐个判断 ii 是不是素数。

假设 ii 是合数，并且 i = prime[j]（最小素因子）* a。

如果 i%prime[j] ==0，那么其后面的合数 i * prime[j+1]=prime[j] * a * prime[j+1]。这个合数可以被后面的 a * prime[j+1] 再乘以素数 prime[j] 筛选出来，即 i*prime[j+1] 这个数的最小质因数不是 prime[j+1]，不能被 prime[j+1] 筛去，所以 i%prime[j] == 0 时要停止。

时间复杂度

因为每个数都只会被筛一遍，因此欧式筛的时间复杂度是严格 O(n)O(n) 的，但相对的它比埃氏筛消耗更多的空间，原理也更难懂一些。

例题1：素数个数（姚班题库1216）

编程求正整数 MM 与 NN 之间的所有素数的个数。（M≤NM≤N）

输入输出格式

输入

两个正整数，分别表示 MM 和 NN。

输出

一个整数，表示素数个数。

输入输出样例

样例

输入1

2 10

Copy

输出1

4

Copy

时间及空间限制

1s, 256MB.

对于 30% 的数据，1 ≤ M ≤ N ≤ 10001≤M≤N≤1000
对于 60% 的数据，1 ≤ M ≤ N ≤ 10000001≤M≤N≤1000000
对于 100% 的数据，1 ≤ M ≤ N ≤ 10000000，N-M ≤ 200001≤M≤N≤10000000，N−M≤20000

如果你能通过前面 10 个测试点，已经很棒了，尝试挑战如下的额外测试点吧！

解法一：常规方法，可得70分

#include
using namespace std;
int main()
{
    long long m,n,i,j,s=0,sum=0;
    cin>>m>>n;
    for(i=m;i<=n;i++)
    {
        s=0;
        for(j=1;j<=i;j++)
        {
            if(i%j==0)
            {
                s++;
            }
        }
        if(s==2) sum++;
    }
    cout<

Copy

解法二：常规优化方法，可得90分

#include
using namespace std;
int main()
{
    long long m,n,i,j,s=0,sum=0;
    cin>>m>>n;
    for(i=m;i<=n;i++)
    {
        s=0;
        for(j=2;j<=sqrt(i);j++)
        {
            if(i%j==0)
            {
                s++;
                if(s>1) break;
            }
        }
        if(s==0) sum++;
    }
    cout<

Copy

解法三：利用素数筛，满分

#include 
using namespace std;
bool a[10000005];   //N的范围 
void prime()       //素数筛优化
{
    a[0] = a[1] = 1;  //0和1不是素数，标记为1 
    for(int i = 2; i <= 10000000; i++)  //从2开始筛选 
    {
        if(a[i] == 0)   //如果是素数，开始筛选其倍数 
        {
            for(int j = i + i; j <= 10000000; j=j+i)  //循环范围需牢记 
            {
                a[j] = 1;  //不是素数 
            }
        }
    }   //数组值为0的都是素数 
}
int main()
{
    prime();//别忘记调用一下筛法，特别重要 
    long long int i,m,n,s=0;
    cin>>m>>n;
    for(i=m;i<=n;i++)
    {
        if(a[i]==0) s++;
    }
    cout<

Copy

例题2：回文素数（主题库2023）

我们将左右对称的自然数成为回文数，例如：121，4114等；将只能被1与其本身整除的自然数称为素数，例如：7，353等。输入n,m，求出n至m(含n和m)之间既是回文数又是素数的自然数共有多少个？

输入格式：文件中只有两个整数 n、m ，且0

输出格式：文件中只有一个整数 ，表示在n和m之间有多少个既是回文数又是素数的自然数。

样例输入：

1 9

Copy

样例输出：

4

Copy

题目分析：

① 自定义判断素数的函数，自定义判断回文的函数；

② 回文：该数正序与逆序都是一样的；

③ 判断该范围内的每一个数是否既是素数又是回文；

④ 记录下素数回文的个数。

很显然需要两个函数，一个判断回文数的，一个判断素数的，判断素数的大家可以用素数筛，接下来就是回文数的函数怎么写？

回文数的函数必须会写，重点使用函数，完整的代码如下所示：

#include 
using namespace std;
bool a[100005];   //N的范围 
void prime()       //素数筛优化
{
    a[0] = a[1] = 1;  //0和1不是素数，标记为1 
    for(int i = 2; i <= 100000; i++)  //从2开始筛选 
    {
        if(a[i] == 0)   //如果是素数，开始筛选其倍数 
        {
            for(int j = i + i; j <= 100000; j=j+i)  //循环范围需牢记 
            {
                a[j] = 1;  //不是素数 
            }
        }
    }   //数组值为0的都是素数 
}
int huiwen(int x)
{
    int a,b=0;
    a=x;
    while(a!=0)
    {
        b=b*10+a%10;
        a=a/10;
    }
    if(x==b) return 1;
    else return 0;
}
int main()
{
    prime();//别忘记调用一下筛法，特别重要 
    int i,n,m,s=0;
    cin>>n>>m;
    for(i=n;i<=m;i++)
    {
        if(a[i]==0&&huiwen(i)==1)   //一个if搞定
        {
            s++;
        }
    } 
    cout<

Copy

例题3：数字游戏（主题库2637）

小莹莹刚学习完约数的知识，一个数的约数指能整除这个数的正整数。周末，小莹莹和几个朋友一起玩耍，刚学习完约数知识的小莹莹迫不及待的想给小朋友们展示一下她的本领，她和几个朋友一起玩起了这样一个游戏:给你一个整数N，需要算出这个数所有的约数的和。例如15的数有1，3，5，15。所以15的约数和为1+3+5+15=24.

输入格式

本题有多组数据，第一行一个T，表示有T组数据;下面T行，每行一个正整数N,表示要处理的数。

输出格式

T行，每行一个正整数，表示输入中对应的数的约数和。

样例输入

1
15

Copy

样例输出

24

Copy

数据范围/约定

对于20%的数据，T=1;

对于50%的数据，T≤5000;

对于80%的数据，T≤50000; .

对于100%的数据，T≤500000,N≤5000000。

解题思路：

完整代码如下：

#include 
using namespace std;
bool a[5000005];   //N的范围，自动清零
void prime()       //素数筛优化
{
    a[0] = a[1] = 1;  //0和1不是素数，标记为1 
    for(int i = 2; i <= 5000000; i++)  //从2开始筛选 
    {
        if(a[i] == 0)   //如果是素数，开始筛选其倍数 
        {
            for(int j = i + i; j <= 5000000; j=j+i)  //循环范围需牢记 
            {
                a[j] = 1;  //不是素数 
            }
        }
    }   //数组值为0的都是素数 
}      
int main()
{
    prime();//别忘记调用一下筛法，特别重要 
    int t, num;
    cin>>t;
    for(int i=1;i<=t;i++)//循环t次
    {
        cin>>num;
        if(a[num] == 0)//如果num为素数，直接输出，不用走下面的for了
        {
            cout<

Copy

例题4：半质数（姚班1560）

上完体育课，小 T 同学去校园超市买了瓶水，喝完后就直接去机房上编程课了，给创 新实验班上编程课的 Q 教练曾经培养出过世界冠军金斌大神，这可是小 T 和他的小伙伴们 的偶象啊！小 T 同学从小学起就一直在金斌学长亲手开发的在线评测系统上提交程序，一 想起小学编程课眼前立刻浮现出 Q 教练的亲切笑容，想起自己初学编程时有些单词如 continue 等总是记不住，每当遇到这种情况 Q 教练总会不厌其烦地拼给自己听。自从进入 初三后小 T 已经有很久没写程序了，也很久没见到和蔼可亲的 Q 教练了，今天这节课来得 太及时了，想到这里小 T 不由加快了脚步，走进机房，只见一阵凉风拍面而来，瞬间让人 神清气爽，原来 Q 教练知道我们上一节是体育课，早开好了空调在等我们了。今天的编程 课 Q 教练一上来就抛给了大家一个高端大气的问题：编程寻找给定范围内的半质数。半质 数小 T 还是第一次听说，这个问题明显比找质数档次高多了！ 质数的定义小 T 早在小学 就知道了，质数又称素数，指在大于 1 的自然数中，只能被 1 和本身整除的数， 也可定 义为只有 1 和本身两个因数的数。而半质数的定义是这样的：若对于一个正整数 N，恰好 能够分解成两个质数的乘积，它就被称为半质数。比如，4=2*2,15=3*5 都是半质数，12 不是半质数，它的质因子分解式为 12=2*2*3，分解出的质数共有 3 个，其中有 2 个质数 2， 1 个质数 3。

输入输出格式

输入

输入数据仅有一行包含两个用空格隔开的正整数 S 和 E，其中 2≤S≤E＜5000000。

输出

输出数据仅有一行包含一个整数表示在 S 到 E 之间共有多少个半质数。

输入输出样例

样例输入1

4 26

Copy

样例输出1

10

Copy

完整代码如下：

#include
using namespace std;
int a[5000010];
void prime()
{
    a[0]=a[1]=1;
    for(int i=2;i<=5000000;i++)
    {
        if(a[i]==0)
        {
            for(int j=i+i;j<=5000000;j=j+i)
            {
                a[j]=1;
            }
        }
    }
} 
int main()
{
    prime();
    long long m,n,s=0;
    cin>>m>>n;
    for(int i=m;i<=n;i++)
    {
        if(a[i]==0) continue;
        for(int j=2;j<=i;j++)
        {
            if(i%j==0)
            {
                if(a[j]==0&&a[i/j]==0)
                {
                    //cout<

Copy