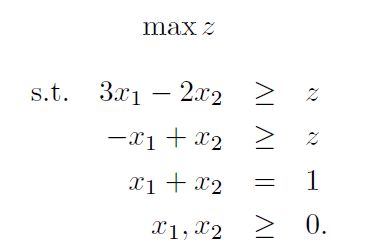多智能体强化学习与博弈论-博弈论基础3

多智能体强化学习与博弈论-博弈论基础3

之前主要介绍了如何判断博弈中是否到达了纳什均衡，在这篇文章中将主要介绍如何计算纳什均衡。

本文主要介绍下列几种情况下的纳什均衡

• 两个智能体，每个智能体有两个动作

• 两个智能体，每个智能体有多个动作，零和博弈

• 非零和，每个智能体有多动作

零和博弈

Minimax Theoram：For every two-person, zero-sum game with finitely many pure strategies, there exists a mixed strategy for each player and a value V such that:

• Given player 2’s strategy, the best possible payoff for player 1 is V
• Given player 1’s strategy, the best possible payoff for player 2 is –V.

当智能体的动作有多个时，我们可以借助线性规划来帮助我们求解。

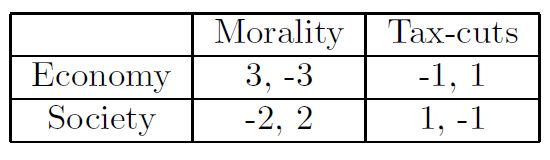
以下面这个情况为例（player1为row player, player2为column player，以两个动作为例）

设player1的策略为，player2的策略为。player2的收益可以表示为

• V（“Morality”）=-3x1+2x2

• V（“Tax-cuts”）=x1-x2

player2的最优收益为max（-3x1+2x2，x1-x2），player1的最优收益为-max（-3x1+2x2，x1-x2）=min（3x1 − 2x2， −x1 + x2）。

我们可以使用下面的这个线性规划来求解player1的最优策略。

同理我们也可以使用下面的这个线性规划来求解player2的最优策略。

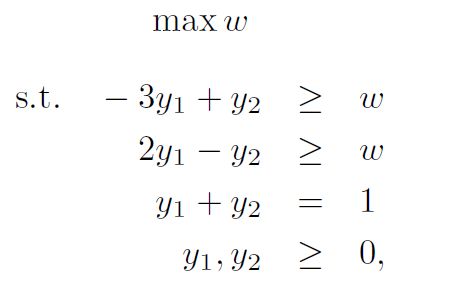
线性规划中的对偶性

每一个线性规划问题都有一个对应的线性规划问题被称为对偶问题，对偶问题对于原问题的求解在很多时候都有着重要的作用。原问题和对偶问题的关系如下图所示。

例子：

强对偶性：由前面我们可以知道

$$\begin{gathered} yAx\le yb \\ yAx\ge cx \end{gathered}$$

可以推出

$$cx\le yAx\le yb$$

当满足

$$cx=yAx=yb$$

则称原问题和对偶问题的关系为强对偶。

原问题对偶的对偶为原问题。

非零和博弈

当我们面对的问题不是零和博弈问题时，往往不能使用线性规划来求解，而是将问题建模成线性互补问题（linear complementarity problem (LCP)）.对于这里的线性互补问题，它是没有目标函数的，整个问题是一个可行性问题。

其中$r$为松弛变量,$s_i^j$为player i选择动作j的概率。最后一行的约束称作complementarity condition。这个约束意味着当$s_i^j$>0时$r_i^j=0$。

The Lemke-Howson algorithm

Lemke-Howson algorithm是一个非常知名的用于解决LCP问题的算法，它利用了图论的思想。

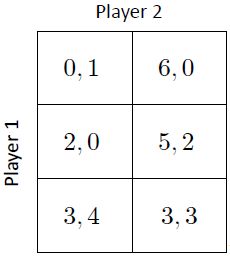
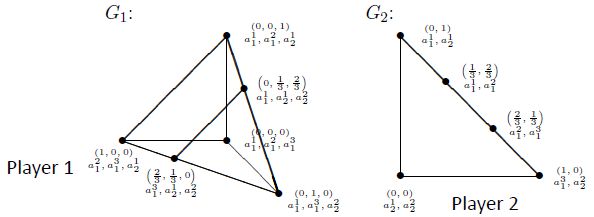
假设有下面这个问题

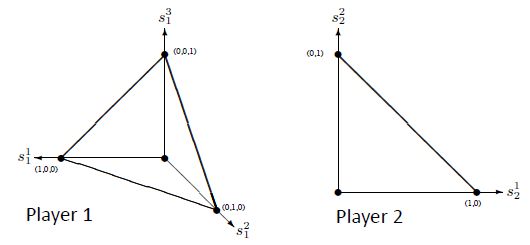
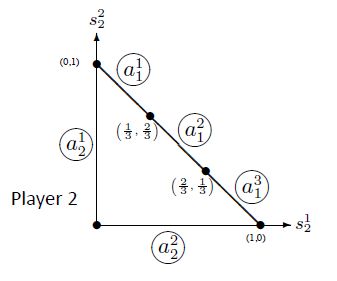
我们可以使用图来表示player的策略，不同坐标轴代表不同的策略。

接着我们需要给player的动作打标签L($s_i^j$ ) ⊆ A1 ∪ A2 。

Mixed strategy si for player i is labeled as follows:

• with each of player i’s actions $a_i^j$ that is not in the support of $s_i$(with zero prob. of choosing it) and

• with each of player −i’s actions $a_{-i}^j$ that is a best response by player −i to $s_i$.

当L(s1) ∪ L(s2) = A1 ∪ A2时我们称这两个策略达到了纳什均衡。

以player2为例，我们可以给player2图像上的边打标签。$a_2^1$代表player2选择动作1的概率为0，$a_1^2$代表player1选择2是针对player2最好的策略。(1/3,2/3)这个点代表如果player2以1/3的概率使用动作1，2/3的概率使用动作2，那么对于player1而言使用动作1和动作2取得的收益都是相同的，以此类推。

我们可以给每个点标号

在这个例子中总共存在三个纳什均衡

[(0, 0, 1), (1, 0)], [(0, 1/3, 2/3) , (2/3, 1/30)] , and [(2/3, 1/3,0) , (1/3, 2/3)]

参考：

汪军老师UCL多智能体强化学习网课