数学建模绘图

数学建模绘图

1. matalb 绘图坐标的处理

i. 设置坐标轴范围

axis([xmin xmax ymin ymax])   % 二维坐标
axis([xmin xmax ymin ymax zmin zmax])  % 三维坐标
axis auto  % 恢复默认

ii. 设置坐标轴纵横比

axis square  % 让x轴与y轴长度相同
axis equal     % 让 x轴与y轴各个刻度线增量的长度相同
axis auto normal  % 恢复默认

iii. 设置坐标轴及网格的可见性

axis on  % 设置坐标轴可见
axis off  %  设置坐标轴隐藏
grid on   % 设置网格可见
grid off   % 设置网格隐藏

Ⅳ. 台南佳坐标轴标签、图形标题及文字信息

xlabel('这里输入x轴标签‘）
ylabel('这里输入y轴标签’）
title('这里输入标题')
text(0,0,'输入要提示的信息文字’）  % 前两个参数为要输入信息的坐标位置

Ⅴ 其他辅助操作基础

title（’图形名称’）
xlabel（’x轴说明’）
ylabel（’y轴说明’）
text（x，y，’图形说明’）
legend（’图例1’，’图例2’，…）

% 横轴 
x=0:pi/50:2*pi; 
% 曲线数据 
y1=sin(x);  
y2=cos(x); 
% 绘图 
figure 
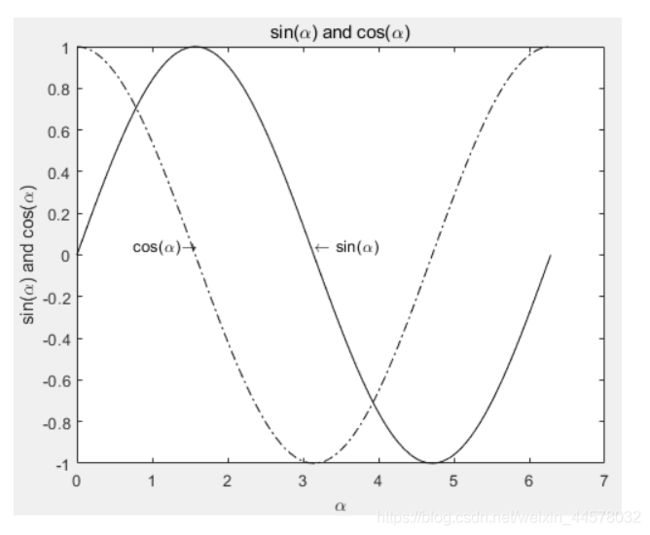
plot(x, y1, 'k-', x, y2, 'k-.') 
% 文本标注 
text(pi, 0.05, '\leftarrow sin(\alpha)') 
text(pi/4-0.05, 0.05, 'cos(\alpha)\rightarrow') 
% 标题标注 
title('sin(\alpha) and cos(\alpha)') 
% 坐标轴标注 
xlabel('\alpha') 
ylabel('sin(\alpha) and cos(\alpha)') 

2. 绘制二维曲线基础

i. plot( ) 函数

plot(x,y)     % 绘制一个y关于x的曲线
plot(x,sin(x),x,2*sin(x))  %  绘制两个或者多个y关于x的曲线

示例代码如下所示：

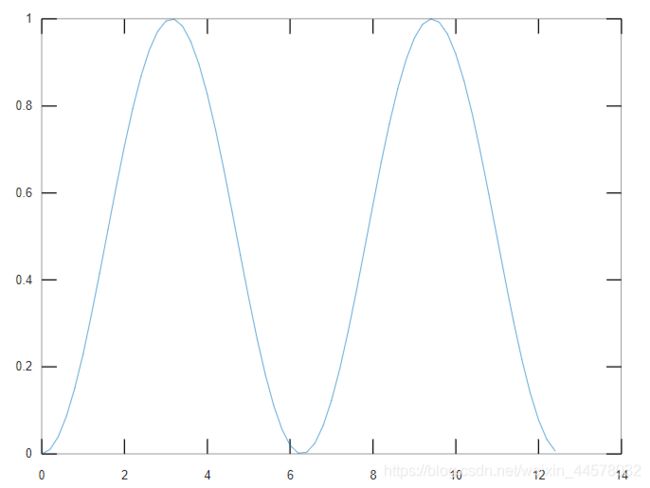
t=0:0.1:2*pi;   % 表示t∈[0，2pi]，采样点间隔为0.1
x=2 * t; 
y=sin(t).*sin(t);   %  .*需要行数列数相等， *满足矩阵运算性质
plot(x, y);

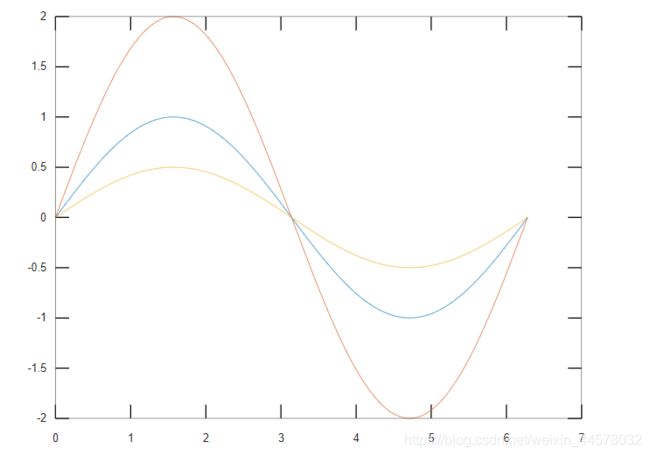
x=linspace(0,2*pi,100);   % 采样点从[0,2pi],采样100个点
plot(x,sin(x),x,2*sin(x),x,0.5*sin(x))   % 在同一坐标纸上绘制三个曲线

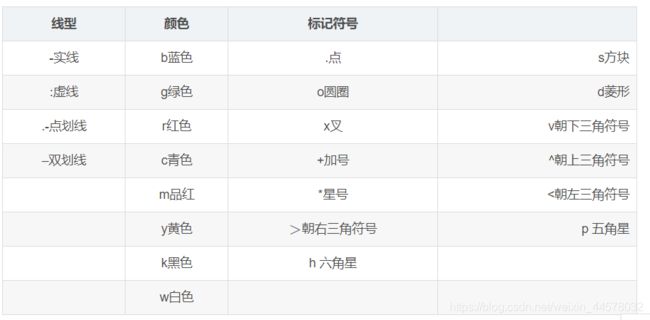
ii. plot() 函数的其他属性设置

属性名称	属性描述
LineWidth	设置线的宽度
MakerSize	设置标记点的大小
MakerEdgeColor	设置标记点的边缘颜色
MakerFaceColor	设置标记点的填充颜色

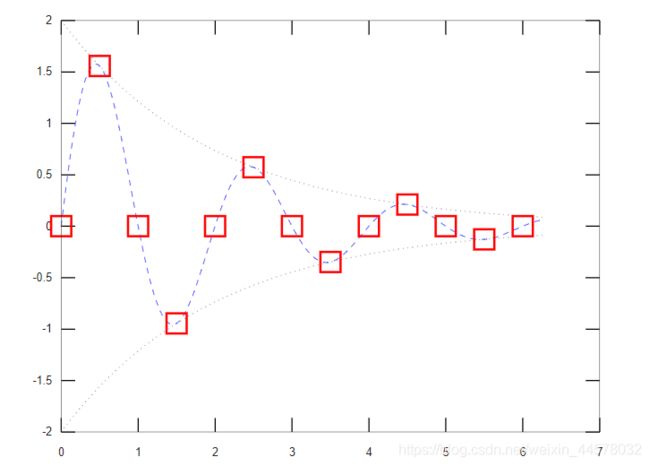
x=(0:pi/100:2*pi)';
y1=2*exp(-0.5*x)*[1,-1];
y2=2*exp(-0.5*x).*sin(pi*x);
x1=(0:12)/2;
y3=2*exp(-0.5*x1).*sin(pi*x1);
plot(x,y1,'k:',x,y2,'b--',x1,y3,'rs'); % 在该图像中，绘制了三个图像，第一个属性描述为’k:‘，为黑丝虚线；  
第二个属性为b--，蓝色双划线；第三个属性为红色方块；`在这里插入代码片`

% 横坐标轴 
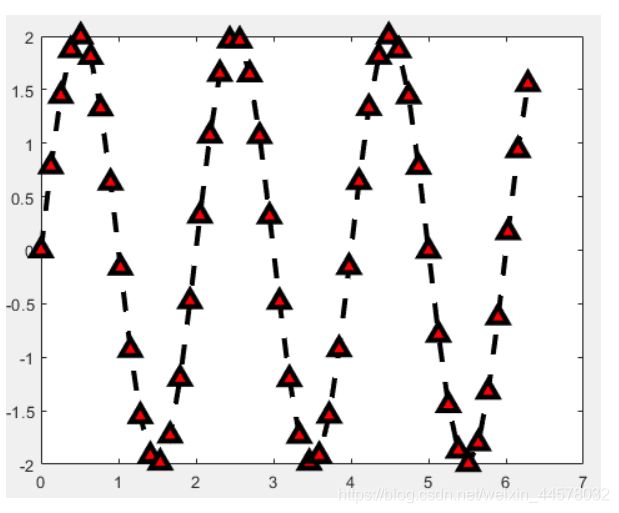
x = linspace(0, 2*pi, 50); 
% 生成数据点，纵坐标轴 
y = 2 * sin(pi * x); 
% 绘图 
figure 
% 设置线的宽带为3 
plot(x, y, 'k--^', 'LineWidth', 3, ...     
    'MarkerEdgeColor', 'k', ...  %设置标记点的边缘颜色为黑色     
    'MarkerFaceColor', 'r', ...  %设置标记点的填充颜色为红色     
    'MarkerSize', 10)    %设置标记点的尺寸为10

% 横坐标轴 
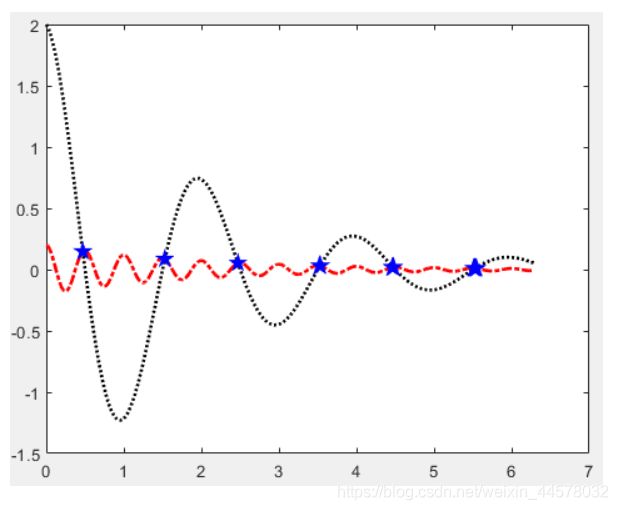
x = linspace(0, 2*pi, 1000); 
% 生成数据点，纵坐标轴 
y1 = 0.2 * exp(-0.5 * x).* cos(4 * pi * x); 
y2 = 2 * exp(-0.5 * x) .* cos(pi * x); 
% 查找y1与y2相等点（近似相等）的下标 
k = find( abs(y1-y2) < 1e-2 );  
%取y1与y2相等点的x坐标 
x1 = x(k);  
% 求y1与y2值相等点的y坐标 
y3 = 0.2 * exp(-0.5 * x1) .* cos(4 * pi * x1);  
% 绘图 
figure 
plot(x, y1, 'r-.', x, y2, 'k:', x1, y3, 'bp','LineWidth',2); 

iii. 双纵坐标函数plotyy()

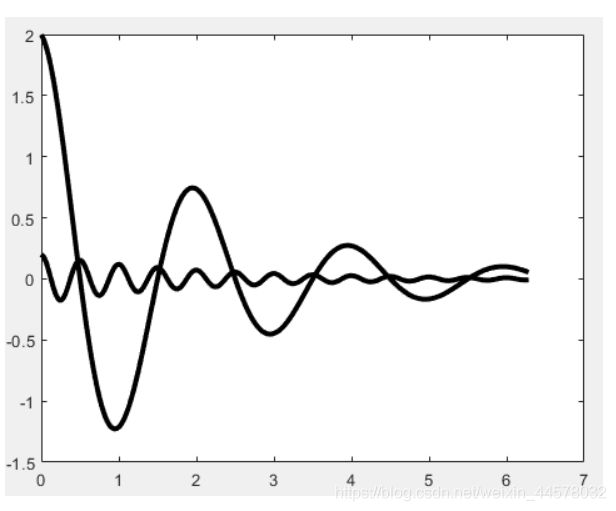
x=0:pi/100:2*pi; 
% 生成曲线 
y1=0.2*exp(-0.5*x).*cos(4*pi*x); 
y2=2*exp(-0.5*x).*cos(pi*x); 
% 绘图 
figure 
plotyy(x,y1,x,y2); 
plot(x, y1, 'k-', x, y2, 'k-', 'LineWidth', 3) 

subplot (m,n,p)   %把窗口分为m×n个绘图区，m行，每一行，n个图，其中p表示为当前活动区。

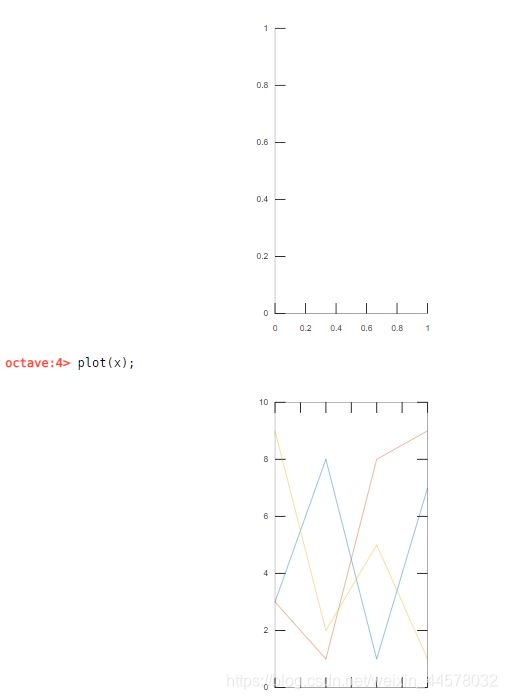
y = [3,7,9,1,5,2,8];   %  一个行向量
subplot(1,2,1);         
plot(y,'linewidth',2);  
grid on;     % 显示网格线

x = [3,3,9;8,1,2;1,8,5;7,9,1];   % 四维3列的矩阵
subplot(1,2,2);
plot(x);

3. 其他二维图形函数基础

i. 对数坐标图

对数坐标图绘制函数格式如下：

semilogx（x1，y1，选项1，x2，y2，选项2，…） % 半对数函数绘制，x轴使用对数刻度，y轴保持线性刻度。
semilogy（x1，y1，选项1，x2，y2，选项2，…） % y轴使用对数刻度，x轴保持线性刻度。
loglog（x1，y1，选项1，x2，yy2，选项2，…） % x与y轴均采用对数刻度

 x轴 
x=0:0.5:5; 
% y轴 
y = exp(x); 
% 绘图 
figure 
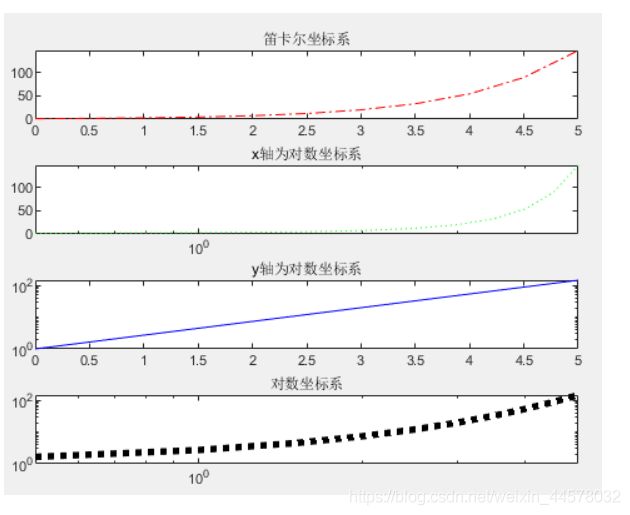
% 笛卡尔坐标系 
subplot(4, 1, 1) 
plot(x, y, 'r-.') 
title('笛卡尔坐标系') 
% 半对数坐标系 
subplot(4, 1, 2) 
semilogx(x, y, 'g:') 
title('x轴为对数坐标系') 
subplot(4, 1, 3) 
semilogy(x, y, 'b-') 
title('y轴为对数坐标系') 
% 对数坐标系 
subplot(4, 1, 4) 
loglog(x, y, 'k:','LineWidth',4) 
title('对数坐标系')

ii. 饼图

pie(x)    % 绘制数据 x 的饼图，x 可以是向量或者矩阵，x 中的每一个元素  
将代表饼图的一个扇区，同时饼图中显示各元素总和的比例。
pie(x, explode)    %  绘制数据 x 的饼图，其中参数 explode 可以用来设置饼图中某个重要的扇区进行抽取式重点显示，  
这里需要注意的是，explode 向量的长度与 x 中的元素个数相等，并与 x 中的元素意义对应，explode 元素为非零值  ，  
对应的元素扇区将从饼图中分离显示，通常非零值都设置为 1.
pie(x, labels)    % 绘制数据 x 的饼图，其中参数 labels 可以用来设置饼图中各个扇区的显示标注，  
注意参数 labels 应该为字符串或者数字利用向量 X中的数据描绘饼图	

代码示例如下：

% 数据准备 
x=[190 33 45 42 45]; 
% 分离显示设置 
explode=[1 1 0 0 0]; 
% 绘图 
figure() 
colormap hsv 
pie(x,explode,{'生活费','资料费','电话费','购买衣服','其他费用'}) 
title('饼图')

Ⅲ 条形统计图

%随机函数产生5*3的数组，对产生的数据取整 
Y = round(rand(5,3)*10);  
% 绘图 
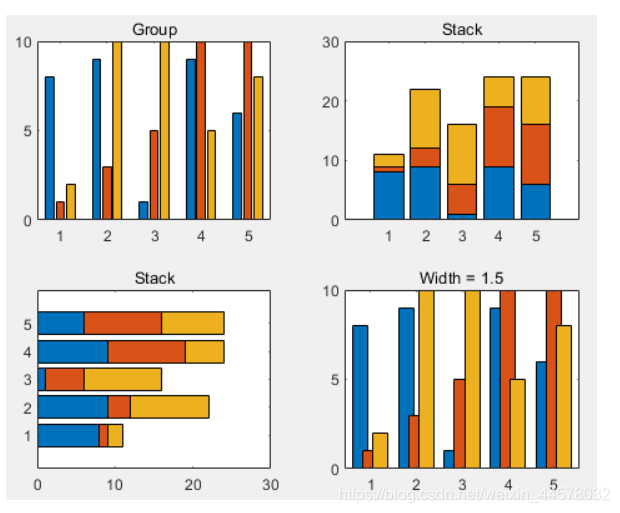
subplot(2,2,1) 
bar(Y,'group') 
title 'Group' 
%堆型二维垂直条形图 
subplot(2,2,2) 
bar(Y,'stack') 
title('Stack') 
%堆型二维水平条形图 
subplot(2,2,3) 
barh(Y,'stack') 
title('Stack') 
%设定条形的宽度为1.5 
subplot(2,2,4) 
bar(Y,1.5) 
title('Width = 1.5') 

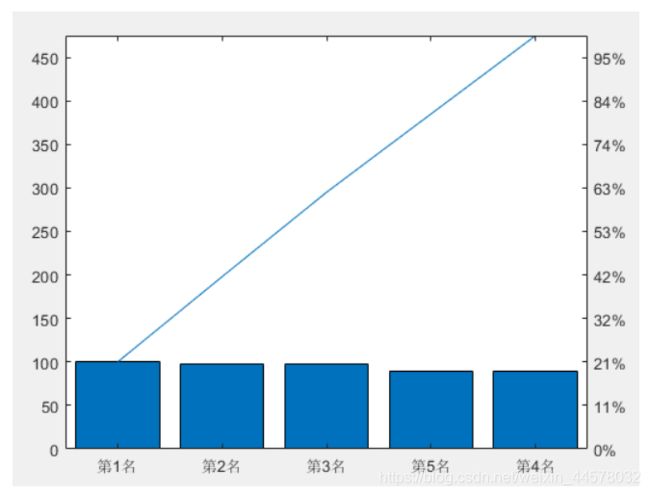
Ⅳ 排列图

Y=[100 98 97 90 90]; 
names={'第1名' '第2名' '第3名' '第4名' '第5名'}; 
pareto(Y,names) 

4 三维图形绘图基础

i. 绘制三维曲线

**plot3()**函数：

plot3（x1，y1，z1，选项1，x2，y2，z2，选项2，…）

其中每一组x，y，z组成一组曲线的坐标参数，选项的定义和plot的选项一样。当x，y，z是同维向量时，则x，y，z对应元素构成一条三维曲线。当x，y，z是同维矩阵时，则以x，y，z对应列元素绘制三维曲线，曲线条数等于矩阵的列数。

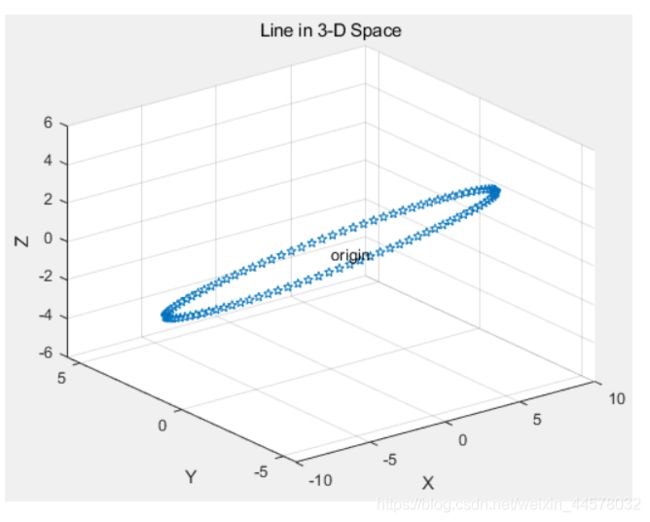
t=0:pi/50:2*pi;
x=8*cos(t);
y=4*sqrt(2)*sin(t);
z=-4*sqrt(2)*sin(t);
plot3(x,y,z,'p');
title('Line in 3-D Space');
text(0,0,0,'origin');
xlabel('X');ylabel('Y');zlabel('Z');grid;

ii. 三维网格图的绘制

[X,Y,Z]=meshgrid(x,y,z)    %  生成向量 x、y、z 的三维网格数据，生成的数据 X 和 Y 可分别表示三维绘图中的 x 和 y 坐标。
mesh(x,y,z)    %  绘制三维网格图，x、y、z 分别表示三维网格图形在 x 轴、y 轴和 z 轴 的坐标，图形的颜色由矩阵 z 决定
mesh(Z)    %  绘制三维网格图，分别以矩阵 Z 的列下标、行下标作为三维网格图的 x 轴、y 轴的坐标，图形的颜色由矩阵 Z 决定

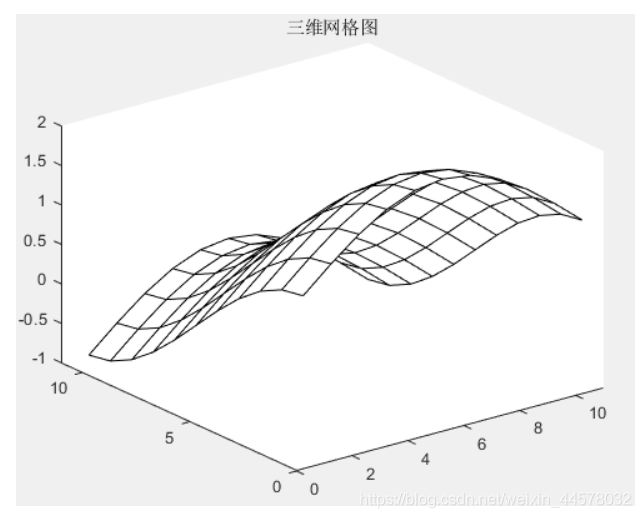
% 数据准备 
t=0:pi/10:pi; 
x=sin(t); 
y=cos(t);  
[X,Y]=meshgrid(x,y); 
z =X + Y;    
% 绘图 
figure 
mesh (z,'FaceColor','W','EdgeColor','K')
grid 
title('三维网格图'); 

iii. 三维表面图的绘制

surf(z)   %  绘制数据 Z 的三维表面图，分别以矩阵 Z 的列下标、行下标作为三维网格图的 x 轴、y 轴的坐标，图形的颜色由矩阵 Z 决定
surf(x,y,z)  %  绘制三维表面图，X、Y、Z 分别表示三维网格图形在 x 轴、y 轴和 z 轴的坐标，图形的颜色由矩阵 Z 决定
surf(..., 'PropertyName', PropertyValue)    %  绘制三维表面图，设置相应属性的属性值

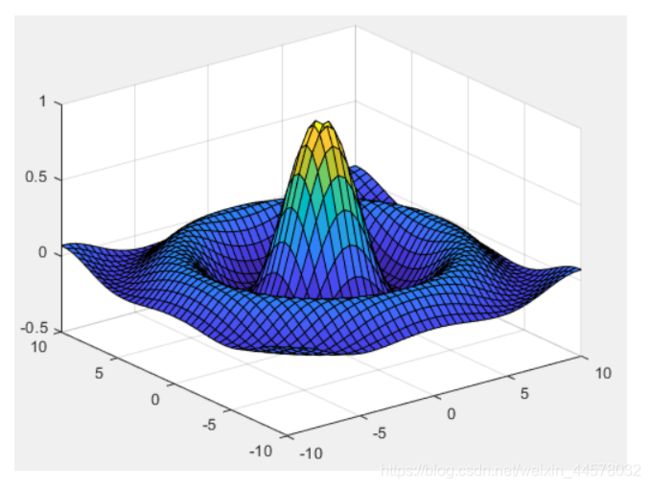
% 数据准备 
xi=-10:0.5:10; 
yi=-10:0.5:10; 
[x,y]=meshgrid(xi,yi); 
z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2); 
% 绘图 
surf(x,y,z)

最后，很感谢博主,此处提供链接地址：https://blog.csdn.net/sunyueqinghit/article/details/81905509