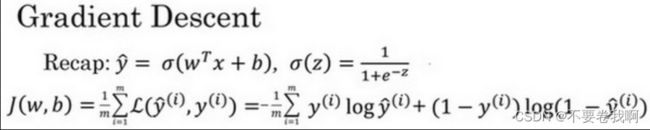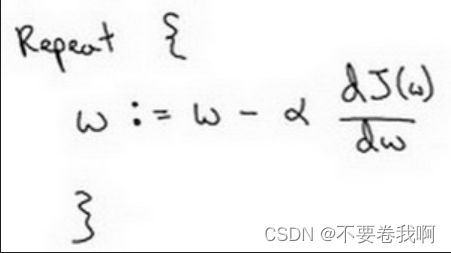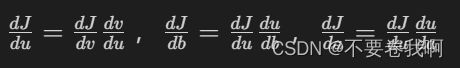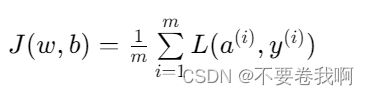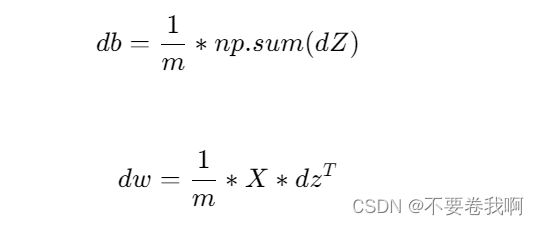【学习周报】深度学习笔记第二周
学习目标:
- 吴恩达深度学习课程week2
学习内容:
- 梯度下降法(Gradient Descent)
- 计算图(Computation Graph)
- 逻辑回归中的梯度下降(Logistic Regression Gradient Descent)
- 向量化(Vectorization)
- Python 中的广播(Broadcasting in Python)
学习时间:
- 10.3-10.9
学习产出:
1. 梯度下降法(Gradient Descent)
作用:在你测试集上,通过最小化代价函数(成本函数)J(w,b)来训练的参数w和b。
训练w、b使得最终对于y^的预测更为精确。
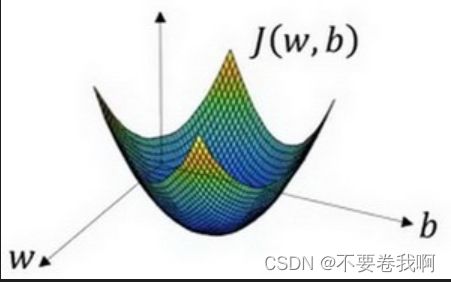
在这个图中,横轴表示你的空间参数w和bb,在实践中,w可以是更高的维度,但是为了更好地绘图,我们定义w和b,都是单一实数,代价函数(成本函数)J(w,b)是在水平轴w和b上的曲面,因此曲面的高度就是J(w,b)在某一点的函数值。
目的:需要寻找一种方法找到J(w,b)的最小值,即最低点。理由:J(w,b)表示的是预测值与真实值之间相差的程度,所以越小就越真实。梯度下降法即为这样一种方法,可以找到J(w,b)的最低点。
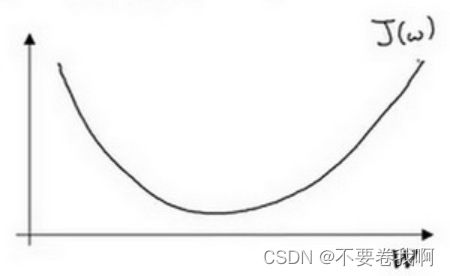
大致过程(以一维函数J(w)为例进行介绍):假设函数J(w)如下图:
为了找到最低点,我们需要不断调整w的值:
其中dJ(w)/dw为函数对w的导数,容易理解,导数斜率的正负以及大小,明显的反映了在该点是在函数的递增还是递减区域,或者说,如果在只有某个极小值的情况下,寻找最低点,即为导数为0的点,我们要做的就是在w导数为正时减小w,导数为负时增大w,不断调整即可找到极值点。
:=表示更新参数,
a 表示学习率(learning rate),用来控制步长(step),即向下走一步的长度dJ(w) /dw就是函数J(w)对w 求导(derivative)
吴老师的讲解视频中还有导数知识:这里不进行解释。
2.计算图(Computation Graph)
使用计算图模拟神经网络的大体思路:前向传播以及反向传播。
首先我们计算出一个新的网络的输出(前向过程),紧接着进行一个反向传输操作。后者我们用来计算出对应的梯度或导数。计算图解释了为什么我们用这种方式组织这些计算过程。
通过一个计算图的实例来模拟神经网络的大体过程:
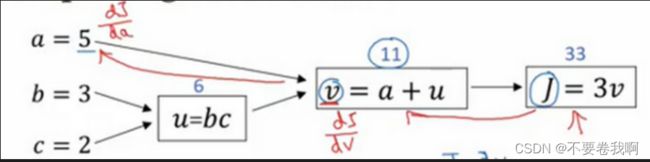
1、计算过程
如上图中,定义函数J = 3(a+bc) 。通过u = bc、v = a+u的换元,我们可以大致画出一个计算图。前向传播即指我们从a、b、c计算得到J值的过程,例如图中输入5、3、2 ,得到J = 33即为前向传播过程。当然这里的过程指a、b、c经过计算得到u、v后逐渐获得中间值,到最终得到J值的过程,毕竟我们指的是神经网络不是数学计算。中间的过程才是我们想突出的重点。
2、反向求导过程
反向求导,旨在求出各个变量对J函数的求导。熟悉链式法则的同学计算起来很简单。
例如求dJ/dv = 3
通过链式法则,容易求出其他变量的导数,这里不再举例。
那么反向传播其实意义就在这里,先求dJ/dv,之后就可以求出dJ/da,如下图的两条红箭头,通过J的反向传播可以影响到a。或者说dJ/da指的就是:如果我们提高a的数值,对J的数值有什么影响?
通过不断反向求出各个变量的导数即为反向传播。
总结:正向计算:从左到右的计算来计算成本函数J。反向传播:从右到左计算导数。
3、逻辑回归中的梯度下降(Logistic Regression Gradient Descent)
梯度下降法、计算图。我们就可以使用计算图对梯度下降算法进行计算。从而解决逻辑回归的某些问题。
正向计算:这个过程根据给出的计算图公式很容易计算。
下面求出的各种导数,使用d+某个字母表示原函数对该字母的相应导数,例如da表示函数L(a,y)对a的偏导数。因为在python中使用da表示简便且易懂。
反向传播:求da:dL(a,y)/da=−y/a+(1−y)/(1−a)
求dz:
具体过程感兴趣可以自己推导。依次可以求出dw1、dw2等
并且可以通过w1:= w1 - a*dw1、w2:= w2 - a*dw2、b:= b - a*db
对参数进行训练,从而得到我们想要的计算模型。
以上是对一个样本的导数计算以及根据训练样本调整参数的过程,如果有m个样本,我们就需要稍微的调整代价函数即可。在开始我们的代价函数代表一个样本与预测函数的相差量,那么m个样本只需要保证各个样本的代价函数之和是最小的即可,即全局的最小值。
新代价函数:(i)表示第i个样本。这里的1/m意义在于m样本代价函数求平均值,但是即使是总代价函数与平均值的极值点是一样的。
同时对于梯度下降不难发现,想要反向传播计算各个导数值,在计算过一个样本的导数值之后可以推理出,只需要对每个样本的导数进行相加即可。
代码流程:
J=0;dw1=0;dw2=0;db=0;
for i = 1 to m
z(i) = wx(i)+b;
a(i) = sigmoid(z(i));
J += -[y(i)log(a(i))+(1-y(i))log(1-a(i));
dz(i) = a(i)-y(i);
dw1 += x1(i)dz(i);
dw2 += x2(i)dz(i);
db += dz(i);
J/= m;
dw1/= m;
dw2/= m;
db/= m;
w=w-alpha*dw
b=b-alpha*db这种计算中有两个缺点,也就是说应用此方法在逻辑回归上你需要编写两个小for循环。第一个for循环是一个小循环遍历m个训练样本,第二个for循环是一个遍历所有特征的for循环。这个例子中我们只有2个特征,所以n等于2。 但如果你有更多特征,你开始编写你的因此dw1,dw2,你有相似的计算从dw3一直下去到dwn。所以看来你需要一个for循环遍历所有n个特征。
其实还有第三个循环,即不断学习的循环,例如规定学习1000次,这种循环一般是不能优化的。
我们说明的两个小循环在计算上有很大的相似性,因此可以考虑放在矩阵中进行运算。下节我们 将考虑向量化:一种减少代码中的显式for循环的操作,可以使得代码的运算效率提升,这在机器学习领域是非常重要的。
4.向量化(Vectorization)
向量化是非常基础的去除代码中for循环的艺术。
在逻辑回归中你需要去计算z=wTx+b,w、x都是列向量。
计算z的一般方法:
z=0
for i in range(n_x):
z += w[i]*x[i]
z += b这样的遍历对于特征量很大(n_x)时非常耗时。
使用向量化:
z=np.dot(w,x)+b这是向量化计算wTx的方法,你将会发现这个非常快。
观察两个简单的长度一百万向量分别用以上两种方法的运行情况:
import numpy as np #导入numpy库
import time #导入时间库
a = np.random.rand(1000000)
b = np.random.rand(1000000) #通过round随机得到两个一百万维度的数组
tic = time.time() #现在测量一下当前时间
#向量化的版本
c = np.dot(a,b)
toc = time.time()
print(c)
print("向量化:" + str(1000*(toc-tic)) +"ms") #打印一下向量化的版本的时间
#非向量化的版本
c = 0
tic = time.time()
for i in range(1000000):
c += a[i]*b[i]
toc = time.time()
print(c)
print("For循环:" + str(1000*(toc-tic)) + "ms")#打印for循环的版本的时间结果:
可以发现计算相同的c用的时间相差三百多倍。
将向量化应用于逻辑回归问题:
正向计算:
Z = np.dot(w.T,X) + b反向传播:
5.Python 中的广播(Broadcasting in Python)
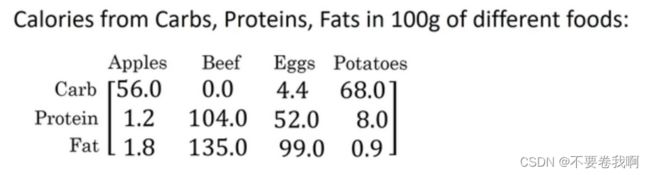
计算各种物质百分比。
import numpy as np #导入numpy库
A = np.array([[56.0,0.0,4.4,68.0],
[1.2,104.0,52.0,8.0],
[1.8,135.0,99.0,0.9]])
print("数据输入:\n",A)
cal = A.sum(axis = 0)
print("列和计算:\n",cal)
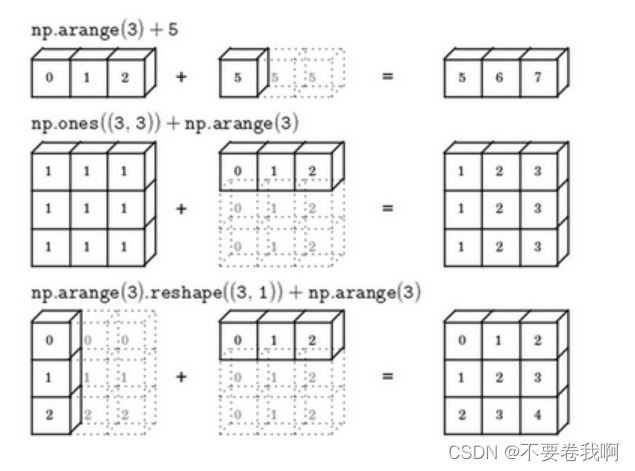
percentage = 100*A/cal.reshape(1,4)#reshape可以去掉,但是为了保证两个数组的维度相同并且计算不
#出错,选自reshape形成合适的矩阵
print("百分比:\n",percentage)cal矩阵自动进行广播,形成3*4的矩阵。
总结: