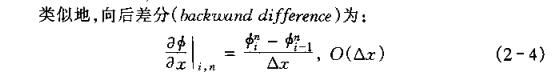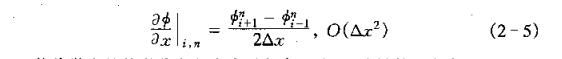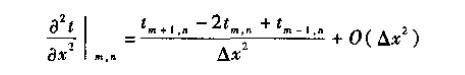Python有限差分法——向前差分,向后差分和中心差分的Python程序
有限差分法
有限差分方法(FDM)是计算机数值模拟最早采用的方法,至今仍被广泛运用。
该方法将求解域划分为差分网格,用有限个网格节点代替连续的求解域。有限差分法以Taylor级数展开等方法,把控制方程中的导数用网格节点上的函数值的差商代替进行离散,从而建立以网格节点上的值为未知数的代数方程组。该方法是一种直接将微分问题变为代数问题的近似数值解法,数学概念直观,表达简单,是发展较早且比较成熟的数值方法。
分类
对于有限差分格式,从格式的精度来划分,有一阶格式、二阶格式和高阶格式。从差分的空间形式来考虑,可分为中心格式和逆风格式。考虑时间因子的影响,差分格式还可以分为显格式、隐格式、显隐交替格式等。目前常见的差分格式,主要是上述几种形式的组合,不同的组合构成不同的差分格式。差分方法主要适用于有结构网格,网格的步长一般根据实际情况和条件来决定。
构造差分的方法
构造差分的方法有多种形式,目前主要采用的是泰勒级数展开方法。其基本的差分表达式主要有三种形式:一阶向前差分、一阶向后差分、一阶中心差分和二阶中心差分等,其中前两种格式为一阶计算精度,后两种格式为二阶计算精度。通过对时间和空间这几种不同差分格式的组合,可以组合成不同的差分计算格式。
Python中调用sympy模块求解差分
from sympy import diff
from sympy import symbols
import sympy
def func(t):
return 2000 * sympy.log(14*10000/(14*10000-2100*t))-9.8*t #函数
t = symbols("t")
print(func(16))
print(diff(func(t),t)) #对函数进行求导
print(diff(func(t),t).subs(t,16))
运行上述程序结果:
392.073691403521
588000000000*(1 - 3*t/200)/(140000 - 2100*t)**2 - 9.8
29.6736842105263
【注意】:
函数的写法不能调用sympy以外的模块的函数
比如这样写就不对:
from sympy import diff
from sympy import symbols
import math
def func(t):
return 2000 * math.log(14*10000/(14*10000-2100*t))-9.8*t
t = symbols("t")
print(func(16))
print(diff(func(t),t))
print(diff(func(t),t).subs(t,16))
结果:
392.07369140352074
print(diff(func(t),t))
return 2000 * math.log(14*10000/(14*10000-2100*t))-9.8*t
raise TypeError("can't convert expression to float")
TypeError: can't convert expression to float
错误点在于:sympy的模块的函数不能调用math模块的函数
一阶向前差分
import sympy
from sympy import diff
from sympy import symbols
#差分的对象
x = 16
k = 2 #步长
x1 = x + k #向前
x2 = x - k #向后
#方程式
def func(t):
return 2000 * sympy.log(14*10000/(14*10000-2100*t))-9.8*t
#一阶向前差分
def for_difference():
a_for_diff = (func(x1) - func(x))/k
for_error = abs(a_for_diff - a_true)/a_true
print(f'{x}的一阶向前差分值:{a_for_diff}')
print(f'{x}的一阶向前差分的误差:{for_error*100}%')
if __name__ == '__main__':
t = symbols("t")
a_true = diff(func(t), t).subs(t, x) # 真值
for_difference()
结果:
16的一阶向前差分值:30.4738991379398
16的一阶向前差分的误差:2.69671578943888%
一阶向后差分
import sympy
from sympy import diff
from sympy import symbols
#差分的对象
x = 16
k = 2 #步长
x1 = x + k #向前
x2 = x - k #向后
#方程式
def func(t):
return 2000 * sympy.log(14*10000/(14*10000-2100*t))-9.8*t
#一阶向后差分
def beh_difference():
a_beh_diff = (func(x) - func(x2))/k
beh_error = abs(a_beh_diff - a_true)/a_true
print(f'{x}的一阶向后差分值:{a_beh_diff}')
print(f'{x}的一阶向后差分的误差:{beh_error*100}%')
if __name__ == '__main__':
t = symbols("t")
a_true = diff(func(t), t).subs(t, x) # 真值
beh_difference()
运行结果:
16的一阶向后差分值:28.9145121806904
16的一阶向后差分的误差:2.55840166138381%
一阶中心差分
import sympy
from sympy import diff
from sympy import symbols
#差分的对象
x = 16
k = 2 #步长
x1 = x + k #向前
x2 = x - k #向后
#方程式
def func(t):
return 2000 * sympy.log(14*10000/(14*10000-2100*t))-9.8*t
#一阶中心差分
def cen_difference():
a_cen_diff = (func(x1)-func(x2))/(k*2)
cen_error = abs(a_cen_diff - a_true)/a_true
print(f'{x}的二阶中心差分值:{a_cen_diff}')
print(f'{x}的二阶中心差分的误差:{cen_error*100}%')
if __name__ == '__main__':
t = symbols("t")
a_true = diff(func(t), t).subs(t, x) # 真值
cen_difference()
代码运行结果:
16的二阶中心差分值:29.6942056593151
16的二阶中心差分的误差:0.0691570640275347%
二阶中心差分
import sympy
from sympy import diff
from sympy import symbols
#差分的对象
x = 16
k = 2 #步长
x1 = x + k #向前
x2 = x - k #向后
#方程式
def func(t):
return 2000 * sympy.log(14*10000/(14*10000-2100*t))-9.8*t
#二阶中心差分
def two_cen_difference():
a_cen_diff = (func(x1)+func(x2)-2*func(x))/(k**2)
cen_error = abs(a_cen_diff - a_true)/a_true
print(f'{x}的二阶中心差分值:{a_cen_diff}')
print(f'{x}的二阶中心差分的误差:{cen_error*100}%')
if __name__ == '__main__':
t = symbols("t")
a_true = diff(func(t), t , 2).subs(t, x) # 求2阶导真值
two_cen_difference()
程序运行结果:
16的二阶中心差分值:0.779693478624694
16的二阶中心差分的误差:0.0779896119162236%
迭代直到精确要求——以一阶向前差分为例
要求初始步长为2,经过多次迭代,一阶向前差分的误差能小于1%
Python代码如下:
import sympy
from sympy import diff
from sympy import symbols
#方程式
def func(t):
return 2000 * sympy.log(14*10000/(14*10000-2100*t))-9.8*t
#一阶向前差分
def for_difference(x1,x,a_true,k):
a_for_diff = (func(x1) - func(x))/k
for_error = abs(a_for_diff - a_true)/a_true
print(f'{x}的一阶向前差分值:{a_for_diff}')
print(f'{x}的一阶向前差分的误差:{for_error*100}%')
return for_error
def Judge_precision(x):
D = True
k = 2 # 初始步长
n = 0
while D:
n += 1
x1 = x + k # 向前
t = symbols("t")
a_true = diff(func(t), t).subs(t, x)
error = for_difference(x1,x,a_true,k)
if error <= 0.01:
D = False
print(f'迭代第{n}次后,{x}的一阶向前差分的误差为{error}')
else:
k = k/2
if __name__ == '__main__':
x = 16 #差分对象
Judge_precision(x)
运行结果:
16的一阶向前差分值:30.4738991379398
16的一阶向前差分的误差:2.69671578943888%
16的一阶向前差分值:30.0684298016344
16的一阶向前差分的误差:1.33028844112341%
16的一阶向前差分值:29.8697466293837
16的一阶向前差分的误差:0.660728265039121%
迭代第3次后,16的一阶向前差分的误差为0.00660728265039121