【数字图像处理学习随笔】图像变换

数字图像处理

---

一、图像变换简介

1.1 图像变换的目的

1. 使图像处理问题简化；
2. 有利于图像特征提取；
3. 有助于从概念上增强对图像信息的理解。

1.2 图像变换的要求

图像变换通常是一种二维正交变换。一般要求：

1. 正交变换必须是可逆的；
2. 正变换和反变换的算法不能太复杂；
3. 正交变换的特点是在变换域中图像能量将集中分布在低频率成分上，边缘、线状信息反映在高频率成分上，有利于图像处理。

1.3 频域滤波

频域滤波实际上就是图像变换的一种方式，简单来说，就是将原始图像先转换到频率域，在频率域对原图像的频谱进行处理，对经过频域处理后的图像，再进行频域反变换，转换回空域，从而达到对原图像进行处理的目的。

1.4 为什么要在频域进行图像处理

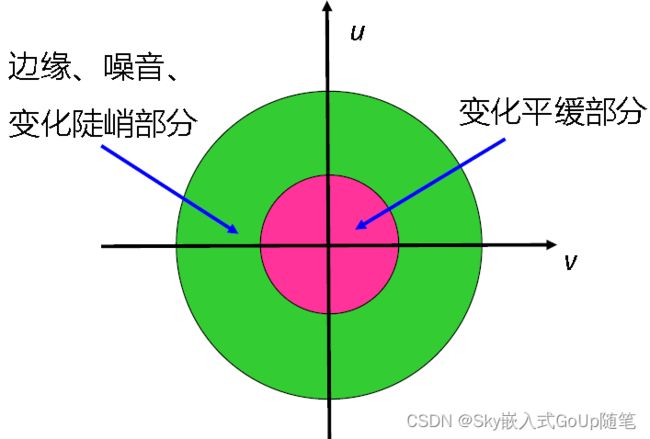
在频域进行图像处理的关键是频率平面与图像空域特性的关系。
在频域空间中，图像变化平缓的部分靠近频率平面的圆心，这个区域为低频区域。
图像中的边缘、噪声、变化陡峻的部分，以放射方向离开频率平面的圆心，这个区域为高频区域。

---

二、频域增强基本原理

在频率空间，图像的信息表现为不同频率分量的组合。如果能让某个范围内的频率分量受到抑制，而让其他分量不受影响，就可以改变输出图像的频率分布，达到不同的增强目的。

---

三、频域滤波基本步骤

频域滤波的原理图如下图所示。

频域滤波的步骤如下图所示。

---

四、低通（平滑）滤波器

4.1 频率域平滑滤波器基本思想

图像中的边缘和其它灰度变化剧烈的部分主要处于傅里叶变换后的高频部分。
平滑可以通过衰减指定图像傅里叶变换中高频成分的范围来实现。
低通平滑滤波器这里主要介绍三种，分别为理想低通滤波器、Butterworth低通滤波器、Gaussian低通滤波器。

4.2 三种低通滤波器的比较

4.2.1 理想低通滤波器(ILPF)

理想——指小于D0的频率可以完全不受影响地通过滤波器，而大于D0的频率则完全通不过。

优点：

• 在半径为D0的圆内，所有频率没有衰减的通过滤波器，而在此半径的圆之外的所有频率完全被衰减掉。
  缺点：
• 由于高频成分包含有大量的边缘信息，因此采用该滤波器在去噪声的同时将会导致边缘信息损失而使图像变模糊。
• 振铃效应：在2-D图像上表现为一系列同心圆环; 圆环半径反比于截断频率。
• 实际当中不可实现。

4.2.2 Butterworth低通滤波器（BLPF）

优点：

• 物理上可实现（理想低通滤波器在数学上定义得很清楚，在计算机模拟中也可实现，但在截断频率处直上直下的理想低通滤波器是不能用实际的电子器件实现的）。
• 减少振铃效应，高低频率间的过渡比较光滑。
• 相对理想滤波器而言，采用该滤波器滤波在抑制噪声的同时，图像边缘的模糊程度大大减小。

缺点：当阶数很高时，平滑作用大，但振铃效应也更加明显，平滑效果会减弱。

用途：图像由于量化不足产生虚假轮廓时常可用低通滤波进行平滑以改进图像质量。

4.2.3 Gaussian低通滤波器（GLPF）

优点：

• 高斯低通滤波器的傅里叶反变换也是高斯的，这也意味着通过计算上式的傅里叶反变换而得到的空间高斯滤波器将没有振铃。

缺点：

• GLPF不能达到有相同截止频率的二阶BLPF的平滑效果
• 如果需要严格控制低频和高频之间截至频率的过渡，选用BLPF，但是代价是可能产生振铃

---

五、MATLAB代码实现

5.1 理想低通滤波器

%%%%%%%%%%%%% 理想 %%%%%%%%%%%%%%%%%%%%%%
s=fftshift(fft2(im2double(I)));
[a,b]=size(s);
a0=round(a/2);
b0=round(b/2);
d0=50; % 将理想低通滤波器的截止频率D0设置为50
for i=1:a %双重for循环计算频率点(i,j)与频域中心的距离D(i,j)=sqrt((i-round(a/2)^2+(j-round(b/2)^2))
    for j=1:b 
        distance=sqrt((i-a0)^2+(j-b0)^2);
        if distance<=d0  % 根据理想低通滤波器产生公式,当D(i,j)<=D0,置为1
            h=1;
        else
            h=0;        % 根据理想低通滤波器产生公式,当D(i,j)>D0,置为0
        end
        s(i,j)=h*s(i,j);% 频域图像乘以滤波器的系数
    end
end
% real函数取元素的实部
s=real(ifft2(ifftshift(s)));% 最后进行二维傅里叶反变换转换为时域图像
subplot(2,3,4),imshow(s,[]);
title('理想低通滤波所得图像'); 

5.2 Butterworth滤波器

%%%%%%%%%%%%% Butterworth %%%%%%%%%%%%%%%%%%%%%%
s=fftshift(fft2(im2double(I)));
[N1,N2]=size(s);%求二维傅里叶变换后图像大小
n=2;            % 将巴特沃斯低通滤波器的阶数n设置为2
d0=50;          % 将巴特沃斯低通滤波器的截止频率D0设置为50
n1=round(N1/2);
n2=round(N2/2);
for i=1:N1      %双重for循环计算频率点(i,j)与频域中心的距离D(i,j)=sqrt((i-round(N1/2)^2+(j-round(N2/2)^2))
    for j=1:N2 
        distance=sqrt((i-n1)^2+(j-n2)^2);
        if distance==0 
            h=0; 
        else
            h=1/(1+(distance/d0)^(2*n));% 根据巴特沃斯低通滤波器公式为1/(1+[D(i,j)/D0]^2n)
        end
        s(i,j)=h*s(i,j);% 频域图像乘以滤波器的系数
    end
end
% real函数取元素的实部
s=real(ifft2(ifftshift(s)));% 最后进行二维傅里叶反变换转换为时域图像
subplot(2,3,5),imshow(s,[]);
title('Butterworth低通滤波图像');

5.3 Gaussian低通滤波器

%%%%%%%%%%%%% Gaussian %%%%%%%%%%%%%%%%%%%%%%
s=fftshift(fft2(im2double(I)));
[a,b]=size(s);
d0=50; % 将高斯低通滤波器的截止频率D0设置为50
a1=round(a/2);
b1=round(b/2);
for i=1:a
    for j=1:b
        distance=sqrt((i-a0)^2+(j-b0)^2);    % 根据高斯低通滤波器公式H(u,v)=e^-[D^2(u,v)/2*D0^2] 
        h=exp(-(distance*distance)/(2*(d0^2))); % exp表示以e为底的指数函数
        s(i,j)=h*s(i,j);% 频域图像乘以滤波器的系数
    end
end

s=real(ifft2(ifftshift(s)));% 最后进行二维傅里叶反变换转换为时域图像
subplot(2,3,6),imshow(s,[]); 
title('高斯低通滤波图像');