目标检测论文阅读：GFL算法笔记

标题：Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection
会议：NeurIPS2020
论文地址：https://dl.acm.org/doi/abs/10.5555/3495724.3497487
这篇文章是围绕“representation”，也就是“表示”一词进行改进的，这个东西实际上就是检测器最终的输出，也就是head末端的物理对象。文中指出了训练和预测过程中的不匹配的问题，并且解决得非常优美，把Focal Loss进行推广，给单阶段检测器带来无痛涨点（后续的V2版本效果更甚）。读第一遍的过程中有很多词汇把握不好含义，需要精读体会。

Abstract

单阶段检测器基本上是把目标检测分为稠密分类和定位（即边界框回归）两个过程。分类通常用Focal Loss优化，边界框定位一般在Dirac delta分布下学习。单阶段检测器最近的一个趋势是引入一个单独的预测分支来评估定位的质量，预测的质量通过促进分类来提升检测性能。本文深入研究了上述三个基本要素的表示：质量估计、分类和定位。在现有的实践中发现了两个问题：①训练和推理阶段中质量估计和分类的使用不一致；②定位时的Dirac delta分布不够灵活。为了解决这些问题，我们为这些元素设计了新的表示。具体来说，我们将质量估计合并到类别预测向量中，形成联合表示，并用一个向量表示任意分布的边界框位置。改进后的表示消除了不一致的风险，准确地刻画了真实数据灵活的分布，但包含连续型的标签，这超出了Focal Loss的范围。于是我们提出了Generalized Focal Loss（GFL），它将Focal Loss从离散形式推广到连续形式来成功实现优化。在COCO test-dev上，GFL使用ResNet-101主干达到了45.0%AP，超过了SOTA的SAPD（43.5%）和ATSS（43.6%），并且具有更高或者相当的推理速度。

1 Introduction

最近，稠密检测器逐渐引领了目标检测的潮流。在稠密检测器的基础上，研究人员们更关注边界框的表示及其定位的质量估计，在该领域取得了出色的进展。具体来说，边界框表示被建模为简单的Dirac delta分布，并在过去几年被广泛使用。正如FCOS中所推广的那样，预测一个额外的定位质量（例如IoU分数或中心性分数），并在推理过程中，将质量估计与分类置信度相结合（通常是相乘）作为非极大抑制（NMS）排序过程的最终得分时，会给检测精度带来一致性的提高。尽管它们取得了成功，但我们在现有实践中观察到以下问题：

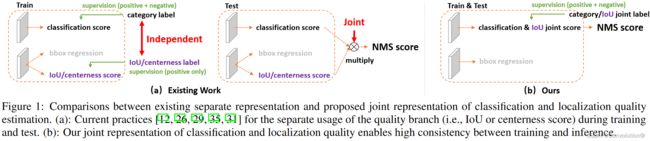
训练和推理阶段中定位质量估计和分类分数的使用不一致： ①最近的稠密检测器中，定位质量估计和分类分数通常是独立训练的，但在推理阶段又被组合使用（比如相乘），如图1a所示；②目前，定位质量估计的监督只针对正样本，这是不可靠的，因为负样本可能得到无法控制的更高质量的预测，如图2a所示。这两个因素造成了训练和测试之间的差距，并有可能降低检测性能，例如，在NMS过程中，具有随机高质量分数的负样本可能会排在预测质量较低的正样本之前。

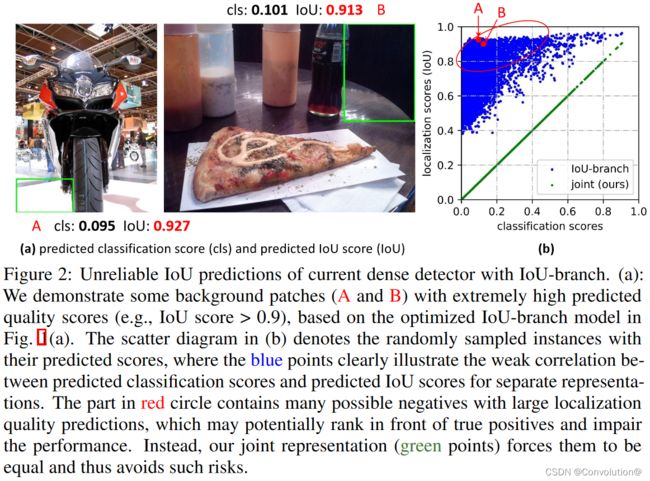
不灵活的边界框表示： 广泛使用的边界框表示可以看作是目标框坐标的Dirac delta分布。然而，它没有考虑数据集中的模糊性和不确定性（图3中目标的不清晰边界）。尽管最近的一些工作将边界框框建模成高斯分布，但它过于简单，无法体现边界框位置的真实分布。实际上，真实的分布会更加随意和灵活，而不需要像高斯函数那样对称。

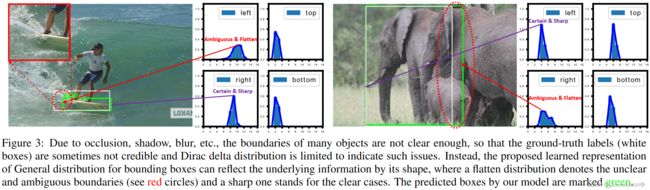
为了解决上述问题，我们为边界框和其定位质量设计了新的表示。对于定位质量表示，我们提出将其与分类分数合并成一个统一的表示：一个分类向量，它在真值类别索引下的值表示其相应的定位质量（通常为本文中预测框和其对应真值框的IoU分数）。通过这种方式，我们将分类分数和IoU分数统一成一个联合且单一的变量（记为“classification-IoU联合表示”），它可以以端到端的方式进行训练，同时直接用于推理阶段，如图1b所示。因此，它消除了训练和测试的不一致性（图1b），使得定位质量和分类之间的相关性最强（图2b）。此外，负样本将以0质量分数进行监督，从而使所有的质量预测变得更加可信和可靠。这对于稠密目标检测器尤其有利，因为它们会对整个图像中均匀采样的所有候选框进行排序。对于边界框表示，我们提出通过直接学习其连续空间上的离散化概率分布来表示边界框位置的任意分布（本文称为通用分布，General distribution），而不引入任何其它更强的先验（如高斯）。因此，我们可以获得更加可靠和精准的边界框估计，同时注意到它们的各种潜在分布（见图3的预测分布）。
然后，这种改进的表示给优化带来了挑战。传统的稠密检测器使用Focal Loss（FL）来优化分类分支。通过改造标准标准交叉熵损失，FL可以成功解决类不平衡问题。然而，对于本文提出的classification-IoU联合表示，除了依旧存在的不平衡风险之外，我们还面临一个新的问题，即需要用连续型的IoU标签$(0\sim 1)$作为监督，而原始的FL仅仅支持离散型的$\{0,1\}$类别标签。通过将$\{0,1\}$离散版本的FL扩展到连续型的变体，我们成功解决了这个问题，称之为Generalized Focal Loss（GFL）。不同于FL，GFL考虑了一种更一般的情况，也就是全局最优解能够以任意期望的连续值为目标，而不是离散值。具体来说，GFL可以细化为Quality Focal Loss（QFL）和Distribution Focal Loss（DFL），分别优化改进后的两种表示：QFL关注难样本的稀疏集，同时在相应的类别上产生连续型的0~1的质量估计；DFL使得网络在任意灵活的分布下，可以快速地关注学习目标边界框连续位置周围值的概率。
我们验证了GFL的三个优势：①它弥补了训练和测试之间的差距，当一个单阶段检测器利用额外的质量估计时，可以使其更加简单、联合和有效地表示分类和定位质量；②它很好地建模了边界框灵活的潜在分布，提供了更多信息丰富和精准的边界框位置；③在不引入额外开销的情况下，可以一致地提高单阶段检测器的性能。在COCO test-dev上，GFL使用ResNet-101主干达到了45.0%AP，超过了SOTA的SAPD（43.5%）和ATSS（43.6%）。我们最好的模型可以在单模型单尺度取得48.2%AP，在单个2080Ti GPU上以10 FPS的速度运行。

2 Related Work

定位质量表示。 现有的一些方法，如Fitness NMS、IoU-Net、MS R-CNN、FCOS和IoU-aware，使用单独的分支，以IoU分数或中心性分数的形式来进行定位质量估计。如第1节所述，这种单独的方式导致了训练和测试之间的不一致以及不可靠的质量预测。PISA和IoU-balance没有引入额外的分支，而是根据各自的定位质量在分类损失中分配不同的权重，旨在增强分类分数与定位精度之间的相关性。然而，这种权重策略是隐式且收益有限的，因为它没有改变分类损失目标的最优性。
边界框表示。 Dirac delta分布支配着过去几年的边界框表示。最近，有一些方法通过引入预测方差，利用高斯假设来学习不确定性。遗憾的是，现有的表示要么过于僵化，要么过于简化，无法反映真实数据中复杂的潜在分布。在本文中，我们进一步放宽假设，直接学习更任意、更灵活的边界框的一般分布，且具有更高的信息量和准确性。

3 Method

本节我们首先回顾单阶段检测器中用于学习稠密分类分数的原始Focal Loss（FL）。然后，我们详细介绍改进的定位质量估计表示和边界框表示，它们分别通过提出的Quality Focal Loss（QFL）和Distribution Focal Loss（QFL）成功优化。最后，我们将QFL和DFL的公式归纳为一个统一的角度——Generalized Focal Loss（GFL），作为FL的灵活扩展，来促进未来进一步的提升和一般性的理解。
Focal Loss（FL）。 原始的FL是针对单阶段目标检测在训练过程中，前景和背景类别之间经常存在极度不平衡的情景而提出的。下面是FL的一种典型形式（出于简化省略了原文中的${\alpha }_t$）：
$$\text{FL}(p)=-(1-p_t{)}^{\gamma }\text{log}(p_t),p_t=\{\begin{array}{ccc}p& ,& wheny=1\\ 1-p& ,& wheny=0\end{array}$$其中，$y\in \{0,1\}$表示真值类别，$p\in [0,1]$表示标签$y=1$的类别的估计概率。$\gamma$是可调节的聚焦参数。具体来说，FL由一个标准交叉熵部分$-\text{log}(p_t)$和一个动态缩放因子部分$(1-p_t{)}^{\gamma }$组成，其中的缩放因子$(1-p_t{)}^{\gamma }$在训练过程中自动降权简单样本的贡献，使模型迅速聚焦到困难样本上。
Quality Focal Loss（QFL）。 为了解决上述训练和测试阶段的不一致问题，我们提出一种定位质量（即IoU分数）和分类分数的联合表示（简称classification-IoU），它的监督软化了标准的one-hot类别标签，使得对应类别可以是一个浮点数标签$y\in [0,1]$（见图4中的分类分支）。具体来说，$y=0$表示质量分数为0的负样本，$0<y\le 1$表示目标IoU分数为$y$的正样本。注意，定位质量标签$y$沿用了传统定义：训练时预测框和其对应真值框的IoU分数，是一个0~1的动态值。我们使用多个带有sigmoid操作$\sigma (\cdot )$的二分类来实现多分类。为简单起见，将sigmoid的输出记为$\sigma$。

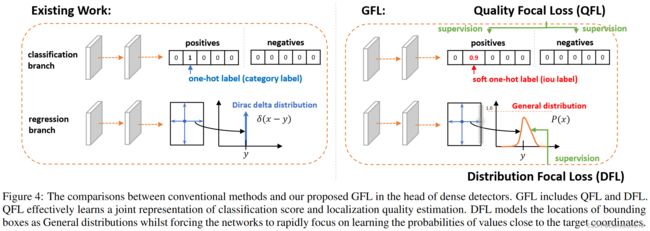
由于提出的分类-IoU联合表示需要对整个图像进行密集的监督，且仍然会出现类不平衡问题，因此必须继承FL的思想。然而，当前形式的FL只支持$0,1$离散标签，而我们的新标签包含小数。因此，我们提出对FL的两个部分进行扩展，使其能够在联合表示的情况下成功训练：①交叉熵部分$-\text{log}(p_t)$扩展成其完整版本$-((1-y)\text{log}(1-\sigma )+y\text{log}(\sigma ))$；②缩放因子部分$(1-p_t{)}^{\gamma }$扩展为估计量$\sigma$和其连续型标签$y$之间的绝对距离，即${\left|y-\sigma \right|}^{\beta }(\beta \ge 0)$，这里$\left|\cdot \right|$保证了非负性。然后，我们将上述两个扩展部分结合起来形成完整的损失目标，称为Quality Focal Loss（QFL）：
$$\text{QFL}(\sigma )=-{\left|y-\sigma \right|}^{\beta }((1-y)\text{log}(1-\sigma )+y\text{log}(\sigma ))$$注意，$\sigma =y$是QFL的全局最小解。当质量标签$y=0.5$时，几个不同$\beta$值下的QFL可视化结果如图5a所示。与FL类似，QFL的${\left|y-\sigma \right|}^{\beta }$项表现为一个调节因子：当一个样本的质量估计不准确且偏离标签$y$时，这个调节因子会相对较大，因此它会更关注学习这个困难样本。当质量估计变得准确（即$\sigma \to y$）时，这个因子会趋向0，简单样本的损失就会降权，其中参数$\beta$平滑地控制了降权速率（我们的实验中$\beta =2$对QFL是最佳的）。

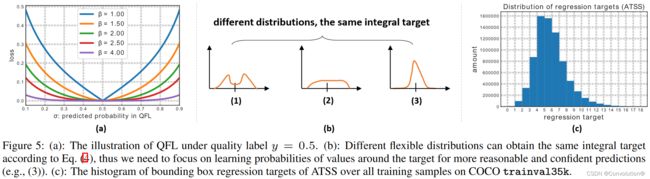
Distribution Focal Loss（DFL）。 我们使用某位置到边界框四条边的相对偏移量作为回归目标（见图4中的回归分支）。传统的边界框回归操作将回归标签$y$建模成Dirac delta分布$\delta (x-y)$，它满足${\int }_{-\infty }^{+\infty }\delta (x-y)\text{d}x=1$，通常用全连接层实现。求解$y$的积分形式如下：
$$y={\int }_{-\infty }^{+\infty }\delta (x-y)x\text{d}x$$根据第1节的分析，不同于Dirac delta或者高斯假设，我们提出直接学习潜在的一般分布$P(x)$而不引入任何先验。给定标签$y$的范围：最小值$y_0$和最大值$y_n$（$y_0\le y\le y_n,n\in {\mathbb{N}}^{+}$），我们可以从模型得到估计值$\hat{y}$（$\hat{y}$也满足$y_0\le \hat{y}\le y_n$）：
$$\hat{y}={\int }_{-\infty }^{+\infty }P(x)x\text{d}x={\int }_{y_0}^{y_n}P(x)x\text{d}x$$为了与卷积神经网络保持一致，我们将连续域上的积分转化为离散表示，把范围$[y_0,y_n]$用均匀间隔$\Delta$离散化成集合$\{y_0,y_1,...,y_i,y_{i+1},...,y_{n-1},y_n\}$，其中$\Delta =y_{i+1}-y_i,\forall i\in [0,n-1]$（出于简单后续实验中我们使用$\Delta =1$）。因此，考虑到离散分布的性质${\sum }_{i=0}^{n}P(y_i)=1$，估计的回归值$\hat{y}$可以表示为：
$$\hat{y}=\sum _{i=0}^{n}P(y_i)y_i$$因此，$P(x)$可以通过由n+1个单元组成的softmax层$S(\cdot )$轻松实现，把$P(y_i)$简记$S_i$。注意，$\hat{y}$可以用传统的损失目标（如SmoothL1、IoU Loss或GIoU Loss）以端到端的方式训练。然而，$P(x)$有无数种取值组合可以使最后的积分结果为$y$，如图5b所示，这可能会降低学习效率。直观上，与FL(公式1)和QFL(公式2)相比，$y$(公式3)的分布是紧凑的，并且在边界框估计上更可信和精准，这促使我们通过显式地鼓励接近目标$y$值的高概率来优化$P(x)$的形状。此外，通常情况下，最合适的潜在位置如果存在的话将不会离粗标签很远。因此，我们引入Distribution Focal Loss，通过显示地增大$y_i$和$y_{i+1}$（最接近$y$的两个值，$y_i\le y\le y_{i+1}$）的概率，迫使网络快速聚焦于接近标签$y$的值。由于边界框的学习只针对正样本，不存在类不平衡问题的风险，因此我们简单地将QFL中的整个交叉熵部分用于DFL的定义：
$$\text{DFL}(S_i,S_{i+1})=-((y_{i+1}-y)\text{log}(S_i)+(y-y_i)\text{log}(S_{i+1}))$$直观上，DFL旨在增大目标$y$周围值（即$y_i$和$y_{i+1}$）的概率。DFL的全局最小解，即$S_i=\frac{y_{i+1}-y}{y_{i+1}-y_i}$，$S_{i+1}=\frac{y-y_i}{y_{i+1}-y_i}$，可以保证估计的回归目标$\hat{y}$无限接近其对应的标签$y$，即$\hat{y}={\sum }_{j=0}^{n}P(y_j)y_j=S_i{y}_i+S_{i+1}{y}_{i+1}=\frac{y_{i+1}-y}{y_{i+1}-y_i}{y}_i+\frac{y-y_i}{y_{i+1}-y_i}{y}_{i+1}=y$，这也保证了其作为一个损失函数的正确性。
Generalized Focal Loss（GFL）。 值得注意的是，QFL和DFL可以统一为一般形式，本文称之为Generalized Focal Loss（GFL）。假设一个模型估计两个变量$y_l$和$y_r$的概率值为$p_{y_l}$和$p_{y_r}$（$p_{y_l}\ge 0,p_{y_r}\ge 0,p_{y_l}+p_{y_r}=1$），其线性组合的最终预测值为$\hat{y}=y_l{p}_{y_l}+y_r{p}_{y_r}(y_l\le \hat{y}\le y_r)$。预测值$\hat{y}$对应的连续型标签$y$也满足$y_l\le y\le y_r$。用绝对距离${\left|y-\hat{y}\right|}^{\beta }(\beta \ge 0)$作为调节因子，GFL的具体形式可写为：
$$\text{GFL}(p_{y_l},p_{y_r})=-{\left|y-(y_l{p}_{y_l}+y_r{p}_{y_r})\right|}^{\beta }((y_r-y)\text{log}(p_{y_l})+(y-y_l)\text{log}(p_{y_r}))$$GFL的性质。 $\text{GFL}(p_{y_l},p_{y_r})$在$p_{y_l}^{\ast }=\frac{y_r-y}{y_r-y_l}$，$p_{y_r}^{\ast }=\frac{y-y_l}{y_r-y_l}$时取得全局最小解，这也意味着估计值$\hat{y}$完美地匹配了它的连续型标签$y$，即$\hat{y}=y_l{p}_{y_l}^{\ast }+y_r$p_{y_r}^*=y$。显然，FL和提出的QFL、DFL都是GFL的特殊情况：

• FL：令GFL中的$\beta =\gamma$，$y_l=0$，$y_r=1$，$p_{y_r}=p$，$p_{y_l}=1-p$，$y\in \{1,0\}$：
  $$\begin{array}{rl}\text{FL}(p)& =\text{GFL}(1-p,p)=-{\left|y-p\right|}^{\gamma }((1-y)\text{log}(1-p)+y\text{log}(p)),y\in \{1,0\}\\ & =-(1-p_t{)}^{\gamma }\text{log}(p_t),p_t=\{\begin{array}{ccc}p& ,& wheny=1\\ 1-p& ,& wheny=0\end{array}\end{array}$$
• QFL：令GFL中的$y_l=0$，$y_r=1$，$p_{y_r}=\sigma$，$p_{y_l}=1-\sigma$：
  $$\text{QFL}(\sigma )=\text{GFL}(1-\sigma ,\sigma )=-{\left|y-\sigma \right|}^{\beta }((1-y)\text{log}(1-\sigma )+y\text{log}(\sigma ))$$
• DFL：将$\beta =0$，$y_l=y_i$，$y_r=y_{i+1}$，$p_{y_l}=P(y_l)=P(y_i)=S_i$，$p_{y_r}=P(y_r)=P(y_{i+1})=S_{i+1}$代入GFL：
  $$\text{DFL}(S_i,S_{i+1})=\text{GFL}(S_i,S_{i+1})=-((y_{i+1}-y)\text{log}(S_i)+(y-y_i)\text{log}(S_{i+1})$$注意，GFL可以用于任意单阶段检测器。改进后的检测器与原始检测器有两个方面的不同。首先，在推理阶段，我们将分类分数（与质量估计的联合表示）作为NMS分数，而不需要乘以任何单独的质量预测（如果存在的话，如FCOS和ATSS中的中心性）。其次，用于预测各个边界框位置的回归分支的最后一层现在有n+1个输出，而不是1个输出，但这带来的额外计算成本可以忽略不计，如表3所示。
  用GFL训练稠密检测器。 我们用GFL定义训练损失$L$：
  $$L=\frac{1}{N_{pos}}\sum _z{L}_Q+\frac{1}{N_{pos}}\sum _z{1}_{\{c_z^{\ast }>0\}}({\lambda }_0{L}_B+{\lambda }_1{L}_D)$$其中，$L_Q$是QFL，$L_D$是DFL。$L_B$一般表示GIoU Loss。$N_{pos}$表示正样本的数量。${\lambda }_0$（通常默认是2）和${\lambda }_1$（实际上是$\frac{1}{4}$，四个方向的平均）分别是$L_Q$和$L_D$的平衡权重。这个和是在金字塔特征图上的所有位置$z$上计算的。$1_{\{c_z^{\ast }>0\}}$是标志函数，如果$c_z^{\ast }>0$则为1否则为0。遵循常见的做法，我们在训练过程中也使用质量分数对$L_B$和$L_D$进行加权。

4 Experiment

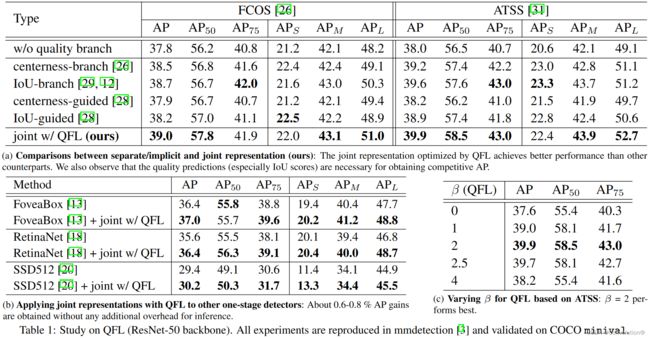
首先验证了QFL的有效性，具体的实验结论可以参照原文。

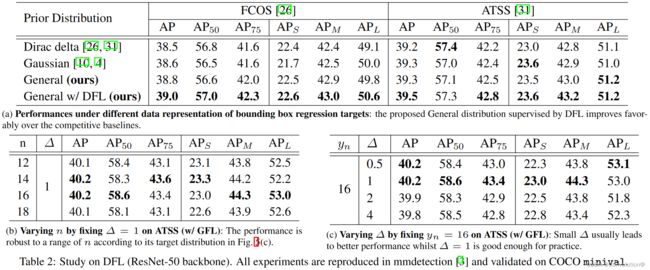
然后验证了GFL的有效性，具体的实验结论可以参照原文。

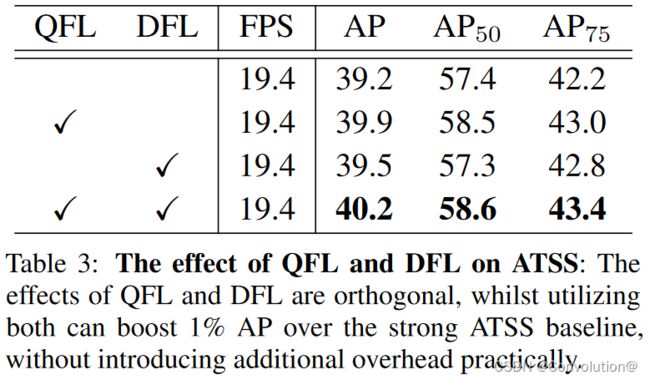
消融实验，QFL和GFL的相对贡献，注意这二者是正交的。具体的实验结论可以参照原文。


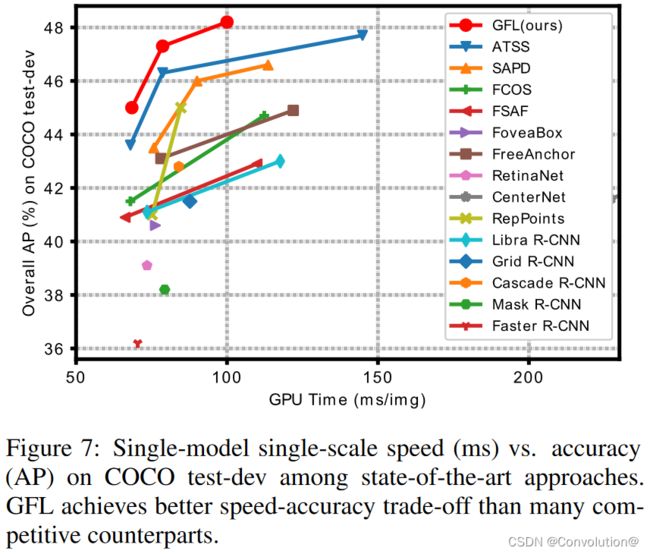
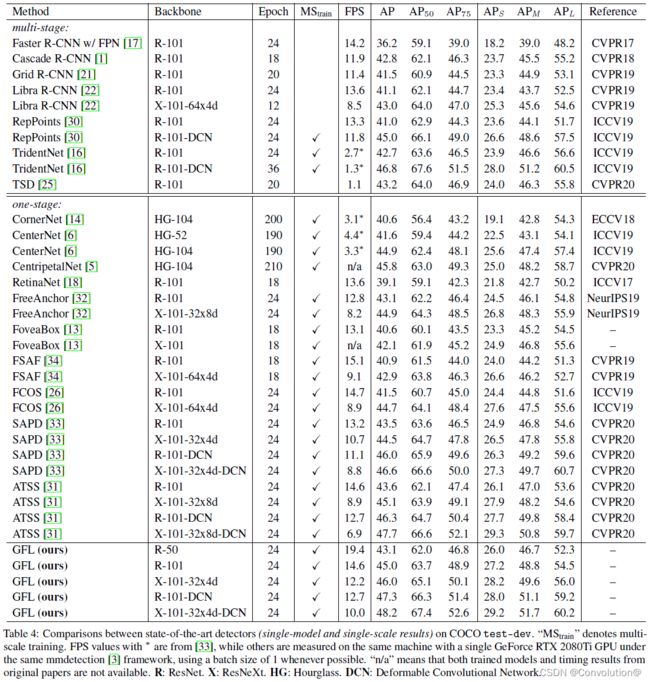
和SOTA对比，具体的实验结论可以参照原文。

5 Analysis

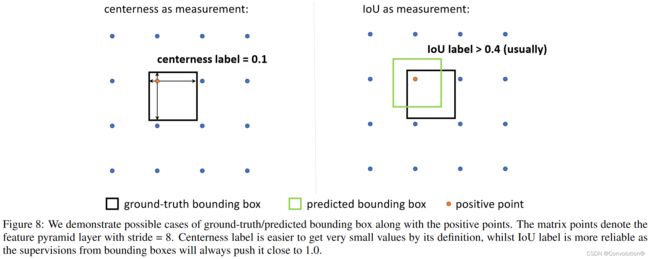
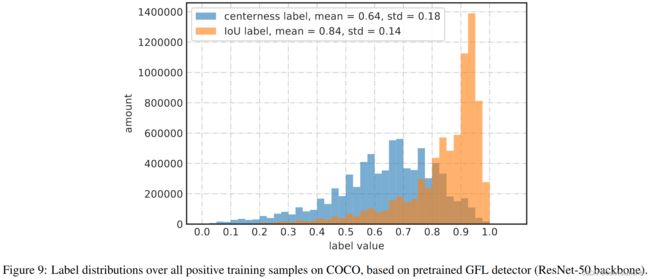
表1的消融实验还表明，对于FCOS/ATSS，作为定位质量的度量，IoU的性能始终要比中心性好。这里我们给出确信的理由。我们发现中心性的主要问题是它的定义导致了意料之外的小真值标签，这使得一组可能的真值边界框极难被召回，如图8所示。从图9所示的标签分布中，我们观察到大部分的IoU标签大于0.4，而中心性标签则倾向于更小（甚至接近0）。中心性标签的小数值阻止了一组真值边界框被召回，它们对NMS的最终得分可能很小，因为它们的预测中心性得分已经被这些极小的信号所监督。

6 Conclusion

为了有效地学习稠密目标检测器的质量和分布式边界框，我们提出了Generalized Focal Loss（GFL），将原始的Focal Loss从$\{1,0\}$离散形式推广到连续形式。GFL可以分为Quality Focal loss（QFL）和Distribution Focal Loss（DFL），其中QFL鼓励学习更好的分类和定位质量的联合表示，而DFL通过将它们的位置建模为一般分布来提供更多信息和更精确的边界框估计。我们还提供了一个令人信服的理由，并建议社区应该使用IoU代替中心性作为质量度量，尽管中心性在FCOS和ATSS中非常成功。大量实验验证了GFL的有效性。我们希望GFL可以作为社区的一个简单而有效的baseline。