从 VDN 到 QMIX的学习笔记
从 VDN 到 QMIX的学习笔记
文章目录
- 从 VDN 到 QMIX的学习笔记
-
- 前言:
- 参考链接:
- VDN的简介:
- 1. 研究背景
- 2.MARL中的难点:
-
- 2.1.部分可观察
- 2.2. 不稳定性
- 3. 为什么要进行值函数分解
- 4. VDN算法的提出:
- 5.VDN的总结:
- 6.QMIX算法:
-
- 6.1 重新认识值函数分解
- 6.2 VDN 的缺点
- 6.3 QMIX 的思想
- 6.4 使用 hypernetworks 去利用全局状态s
- 关于这段网络结构的分析:
- 最后的总结:
- 联系方式:
前言:
这几天看了一下model-based 的dream control,以及multi agent RL的VDN,QMIX,在群友们的帮助下,少走了很多弯路,最后也简单做一个我理解中的小笔记。
由于VDN和QMIX这两个算法,是MARL中非常经典的两篇,因此知乎上和网上都有非常多的教程和博客,我这里贴几份我感觉容易理解的内容。
最后加一下,我看的时候,比较困惑的一个点(可能只有我会困惑…)
参考链接:
-
伏羲讲堂多智能体强化学习中的值函数分解——VDN、QMIX、QTRAN–里面的PDF下载来,认真看,思路非常清晰!有了它,基本上就够了。
-
VDN算法解析: Value-Decomposition Networks For Cooperative Multi-Agent Learning–后面有直接copy博主的内容。
-
【QMIX】一种基于Value-Based多智能体算法–比较详细
-
https://github.com/oxwhirl/pymarl/blob/c971afdceb34635d31b778021b0ef90d7af51e86/src/modules/mixers/qmix.py–直接定位到QMIX的代码
VDN的简介:
copy by [1]:
1. 研究背景
CooperativeMulti-AgentReinforcementLearning最近是一个比较热的研究点,涌现出了许多新奇的算法,主流算法主要分为communication和CentralizedTraining DecentralizedExecution(CTDE)两种。本文将从基本的MARL问题出发,尽可能简明扼要地对CTDE中的各种ValueDecomposition方法(VDN、QMIX、
QTRAN、QPD)进行介绍。
2.MARL中的难点:
2.1.部分可观察
当agent和环境进行交互时,agent无法看到和环境的全局状态s,只能观察到自己视野范围内的局部信息o。
2.2. 不稳定性
在 multi-agent 环境中, 由于 agents 之间相互影响,因此 agent_i 在观察o_i下 执行动u_i后得的r_i与o_i’是由所有 agents 的行为造成的,即r_i = R_i(s,u), o′ = T_i(s, u)。 那么此时对于 agent_i 而言,即使他在观察o_i下一直都执行动作u_i,但 是由于 s 未知且其他 agent 的策略在不断变化,此时 agent_i 得到的r_i和o_i′可能是不同的.
3. 为什么要进行值函数分解
其实简单来说,MARL中的难点就是智能体只能站在自己的角度去观察去决策,无法站在全局的角度去观察并决策,从而无法学到全局最优策略。因此为了解决这个问题,大家提出使用CentralizedTraining DecentralizedExecution(CTDE)的方法,将条件限制放松,允许agents在训练的时候可以访问全局信息,从而站在全局的角度去训练。但是即使能站在全局的角度去训练,你要训练出一个什么形式的策略才行呢?
直观的答案就是去训练一个全局的Q_total(s, u),它考虑了全局信息,可以直接克服MARL中的不稳定性。但是要注意,即使你训练出了Q_total(s, u)又能怎么样呢,部分可观察导致agents在执行的过程中是无法得到s的,也就是说你拥有Q_total(s, u)却无法使用它。说到这里就可以回答上一节提出的问题,部分可观察除了会造成不稳定性,还会导致我们无法直接使用Q_total(s, u),这一点是极为致命的。
此时问题已经很明显了,仅仅使用agent的Q_i(o_i, u_i)进行决策存在不稳定性,而只有Q_total(s, u)才能站在全局的角度进行学习去解决不稳定性,但它得到了又
没办法直接用,因此就出现了一系列值函数分解的方式来解决这个问题。
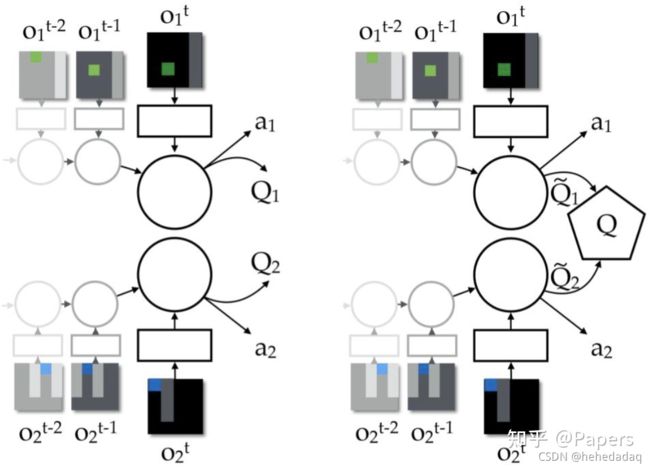
4. VDN算法的提出:
上面说到只有Q_total(s, u)才能站在全局的角度进行学习去,从而解决不稳定性,但是部分可观察的限制使得Q_total(s, u)无法使用。因此 VDN 开创性地提出
使用Q_i(o_i, u_i)对Q_total(s, u)进行分解而不是直接去学习,具体的分解方式为:



5.VDN的总结:
copy by [2]:
VDN算法结构简洁,通过它分解得到的 Q_i 可以让智能体根据自己的局部观测选择贪婪动作,从而执行分布式策略。其集中式训练方式能够在一定程度上保证整体Q函数的最优性。此外,VDN的“端到端训练”和“参数共享”使得算法收敛速度非常快,针对一些简单的任务,该算法可以说既快速又有效。
但是对于一些比较大规模的多智能体优化问题,它的学习能力将会大打折扣。其根本限制在于缺少值函数分解有效性的理论支持。VDN以简单的求和方式将整体Q函数完全分解开,使得多智能体Q网络的拟合能力很受限制。
在下一篇介绍的QMIX[2]算法中,这种端到端训练的思路被继续沿用。作者改善了值函数分解的网络结构,考虑了系统全局状态Q_total 以及分布式策略的单调性约束,有效地增强了网络对整体Q函数的拟合能力。
6.QMIX算法:
6.1 重新认识值函数分解
6.2 VDN 的缺点
我们可以发现 VDN 是将所有的Q_i(o_i, u_i)加起来去近似Q_total(s, u),即认为
Q_i(o_i, u_i)和Q_total(s, u)之间的关系是求和,通过累加和来近似Q_total(s, u)。但是我们知道求和是一种很简单的关系,它不能表示复杂的Q_total(s, u)。如果实际上Q_i(o_i, u_i)和Q_total(s, u)的关系很复杂, 那么 VDN 就没用了。此外,既然我们已经是集中式训练了,那么为什么不尽可 能地利用集中式训练这个优势呢?而 VDN 忽略了学习期间可用的任何额外状态 信息。
6.3 QMIX 的思想
由于 VDN 不能表示复杂的Q_total(s, u), 因此 QMIX 首先提出使用神经网络 f 去近似Q_total(s, u),因为神经网络是具有强大的表示能力的。此外, 由于 VDN 没有尽可能利用集中式训练的优势, 忽略了学习期间可用的任何额外状态信息, 因此 QMIX 在近似Q_total(s, u)时额外使用了全局状态s, 这样就可以基于全局状 态s进行训练,而不是像 VDN 那样仅仅拿Q1,…, Qi去训练。 QMIX 的 Loss 函数 和 VDN 一样, 还是使用 DQN 那一套的 TD-error 来训练。
这样做还存在一个问题, 虽然我们希望通过神经网络f去学习Q_total与 [Q1,…, Qi]之间的关系表示, 但是这并不代表f可以随便学。要注意我们的目的是 学习到好的Q_i(o_i, u_i), f只是为了更好地近似Q_total。如果f是一个很差的关系表 示,那么近似出的Q_total已经不对了,更别说去更新Q_i。因此 QMIX 限制 f 中的参数全部非负,从而确保满足条件:

上面是全文最重要的一个公式,该条件可以让Q_total与Qi之间的关系满呈单调性,从而确保:
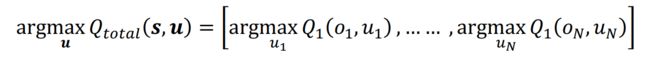
6.4 使用 hypernetworks 去利用全局状态s
关于这段网络结构的分析:
上面所有的复制,都是为了记录下面的这段理解;
对于VDN的网络,它的forward函数非常简单:
import torch as th
import torch.nn as nn
class VDNMixer(nn.Module):
def __init__(self):
super(VDNMixer, self).__init__()
def forward(self, agent_qs, batch):
return th.sum(agent_qs, dim=2, keepdim=True)
但是对于QMIX的,就要复杂一些了。
我们首先要弄明白,代码得实现这个公式:

这个公式表示,所有的Q_i前面的系数最好都不小于0.
如果不管state的话,直接在Q_i求和时,套上一层abs激活函数即可。
但是由于要结合state的信息,因此要走一个比较复杂的信息流:
import torch as th
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
class QMixer(nn.Module):
def __init__(self, args):
super(QMixer, self).__init__()
self.args = args
self.n_agents = args.n_agents
self.state_dim = int(np.prod(args.state_shape))
self.embed_dim = args.mixing_embed_dim
if getattr(args, "hypernet_layers", 1) == 1:
self.hyper_w_1 = nn.Linear(self.state_dim, self.embed_dim * self.n_agents)
self.hyper_w_final = nn.Linear(self.state_dim, self.embed_dim)
elif getattr(args, "hypernet_layers", 1) == 2:
hypernet_embed = self.args.hypernet_embed
self.hyper_w_1 = nn.Sequential(nn.Linear(self.state_dim, hypernet_embed),
nn.ReLU(),
nn.Linear(hypernet_embed, self.embed_dim * self.n_agents))
self.hyper_w_final = nn.Sequential(nn.Linear(self.state_dim, hypernet_embed),
nn.ReLU(),
nn.Linear(hypernet_embed, self.embed_dim))
elif getattr(args, "hypernet_layers", 1) > 2:
raise Exception("Sorry >2 hypernet layers is not implemented!")
else:
raise Exception("Error setting number of hypernet layers.")
# State dependent bias for hidden layer
self.hyper_b_1 = nn.Linear(self.state_dim, self.embed_dim)
# V(s) instead of a bias for the last layers
self.V = nn.Sequential(nn.Linear(self.state_dim, self.embed_dim),
nn.ReLU(),
nn.Linear(self.embed_dim, 1))
def forward(self, agent_qs, states):
bs = agent_qs.size(0)
states = states.reshape(-1, self.state_dim)
agent_qs = agent_qs.view(-1, 1, self.n_agents)
# First layer
w1 = th.abs(self.hyper_w_1(states))
b1 = self.hyper_b_1(states)
w1 = w1.view(-1, self.n_agents, self.embed_dim)
b1 = b1.view(-1, 1, self.embed_dim)
hidden = F.elu(th.bmm(agent_qs, w1) + b1)
# Second layer
w_final = th.abs(self.hyper_w_final(states))
w_final = w_final.view(-1, self.embed_dim, 1)
# State-dependent bias
v = self.V(states).view(-1, 1, 1)
# Compute final output
y = th.bmm(hidden, w_final) + v
# Reshape and return
q_tot = y.view(bs, -1, 1)
return q_tot
公式里提的是要保证dQ_tot/dQ_i>0,这意味着要保证Q_i前面的系数大于0,而不是要保证Q_i大于0.
因此代码里最终forward的函数的Q_tot=hiddenabs(state) + relu(state), hidden= elu(Q_iabs(state)+mlp(relu(state))),这里的abs(state)就是Q_i的系数,即保证了系数大于等于0的效果
另外关于这个网络,它本身还意味着有一个RNN,一般用GRN去实现。
最后的总结:
多智能体我好像用不上,但这个网络结构设计,还蛮有意思的,做一个简单的记录,便于以后查看。
联系方式:
ps: 欢迎做强化的同学加群一起学习:
深度强化学习-DRL:799378128
Mujoco建模:818977608
欢迎玩其他物理引擎的同学一起玩耍~
欢迎关注知乎帐号:未入门的炼丹学徒
CSDN帐号:https://blog.csdn.net/hehedadaq
极简spinup+HER+PER代码实现:https://github.com/kaixindelele/DRLib