Softmax在Fashion-MNIST的实现(手动从0实现 softmax 回归(只借助Tensor和Numpy相关的库))
手动从0实现 softmax 回归
## 加载Fashion-MNIST
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
# 下载数据并将所有数据转换为 ,train为是否训练数据集,download默认网上下载
mnist_train = torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST', train=True, download=False, transform=transforms.ToTensor())
mnist_test = torchvision.datasets.FashionMNIST(root='~/Datasets/FashionMNIST', train=False, download=False, transform=transforms.ToTensor())
# 通过 读取小批量数据样本,shuffle是否打乱顺序,num_workers为进程的个数
batch_size = 256
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=256, shuffle=True, num_workers=1)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=256, shuffle=False, num_workers=1)
## 参数初始化
num_inputs = 784# 拉成向量的长度
num_outputs = 10# 分类的类别个数
W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)# 权重的高斯随机初始化
b = torch.zeros(num_outputs, requires_grad=True) # 偏移的随机初始化
## 网络
# 定义Softmax
def softmax(X):
X_exp = torch.exp(X)
partition = X_exp.sum(1, keepdim=True)# 按行求和
return X_exp / partition # 这里应用了广播机制
# 定义网络 reshape中的-1表示系统帮助计算(结果为256)
def net(X):
return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)
## 交叉熵损失
def loss(y_hat, y):
return -torch.log(y_hat[range(len(y_hat)), y])
## 梯度下降
def sgd(params, lr, batch_size):
for param in params:
param.data -= lr * param.grad / batch_size # 注意这里更改param时用的param.data
## 模型训练
lr = 0.1
num_epochs = 3 # 迭代次数
for epoch in range(num_epochs): # 训练模型一共需要num_epochs个迭代周期
# 在每一个迭代周期中,会使用训练数据集中所有样本一次
for X, y in train_iter: # data_iter返回两个值:特征和标签
l = loss(net(X), y).sum() # l是有关小批量X和y的损失
l.backward() # 小批量的损失对模型参数求梯度
sgd([W, b], lr, batch_size) # 使用小批量随机梯度下降迭代模型参数
W.grad.data.zero_() # 梯度清零
b.grad.data.zero_() # 梯度清零
train_l = loss(net(X), y)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
## 模型测试与实际值比较
import numpy as np
for X, y in test_iter:
print(net(X).size())
a = net(X).detach().numpy()
# print (a)
print (a.argmax(axis=1))
print(y)
交叉熵损失的实现
衡 量 两 个 概 率 分 布 的 差 异 : H p ( q ) = ∑ i q ( i ) l o g 2 ( 1 p ( i ) ) L ( Θ ) = 1 n ∑ 1 n H p ( q ) = − 1 n ∑ 1 n l o g 2 ( p ( j ) ) q ( j ) = 1 的 位 置 ( 由 于 q ( i ) 实 际 概 率 分 布 的 特 点 : 非 零 即 1 ⋅ ) 衡量两个概率分布的差异: H_p(q)=\sum_i q(i)log_2(\frac{1}{p(i)})\\ L(\Theta )=\frac{1}{n}\sum_1^n H_p(q) =-\frac{1}{n}\sum_1^n log_2(p(j))_{q(j)=1的位置}\\(由于q(i)实际概率分布的特点:非零即1·)\\ 衡量两个概率分布的差异:Hp(q)=i∑q(i)log2(p(i)1)L(Θ)=n11∑nHp(q)=−n11∑nlog2(p(j))q(j)=1的位置(由于q(i)实际概率分布的特点:非零即1⋅)
def loss(y_hat, y):
return -torch.log(y_hat[range(len(y_hat)), y]) # 取出真实类别对应的y_hat概率(y为y_hat索引中列元素的索引 )
## 通过索引取值的实现例子
y = torch.tensor([0, 2])
y_hat = torch.tensor([[1, 2, 3], [4, 5, 6]])
y_hat[[0,1], y] # tensor([1, 6])
y_hat[[0,1], [0, 2]] # tensor([1, 6])
结果展示
并从loss、训练集以及测试集上的准确率等多个角度对结果进行分析 (要求从零实现交叉熵损失函数)
import numpy as np
for X, y in test_iter:
print(net(X).size())
a = net(X).detach().numpy()
b = a.argmax(axis=1)
c = y.detach().numpy()
print(b)
print(c)
print(b-c)
np.count_nonzero(b-c)
def accuracy(y_hat, y): #@save
"""计算预测正确的数量。"""
if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
y_hat = y_hat.argmax(axis=1)
cmp = y_hat.type(y.dtype) == y
return float((cmp.type(y.dtype).sum()))
import numpy as np
for X, y in test_iter:
# print(net(X).size())
print(accuracy(net(X), y))
a = net(X).detach().numpy()
b = a.argmax(axis=1)
c = y.detach().numpy()
# print(b)
# print(c)
print(b-c)
lr = 0.1
num_epochs =5 # 迭代次数
for epoch in range(num_epochs): # 训练模型一共需要num_epochs个迭代周期
# 在每一个迭代周期中,会使用训练数据集中所有样本一次
for X, y in train_iter: # data_iter返回两个值:特征和标签
l = loss(net(X), y).sum() # l是有关小批量X和y的损失
l.backward() # 小批量的损失对模型参数求梯度
sgd([W, b], lr, batch_size) # 使用小批量随机梯度下降迭代模型参数
W.grad.data.zero_() # 梯度清零
b.grad.data.zero_() # 梯度清零
train_l = loss(net(X), y)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
print('epoch %d, train-accuracy %f' % (epoch + 1, accuracy(net(X), y)))
for X, y in test_iter:
# print(net(X).size())
print(accuracy(net(X), y))
=====================================================================================
利用torch.nn实现 softmax 回归在Fashion-MNIST数据集上进行训练和测试,并从loss,训 练集以及测试集上的准确率等多个角度对结果进行分析
from torch import nn
# PyTorch不会隐式地调整输入的形状。因此,
# 我们在线性层前定义了展平层(flatten),来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))
def init_weights(m):
if type(m) == nn.Linear: # 如果当前层是线性层 就将当前的参数初始化为默认为0,方差为0.01
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights); # 在网路的每一层运行函数init_weights
loss = nn.CrossEntropyLoss()
trainer = torch.optim.SGD(net.parameters(), lr=0.1)
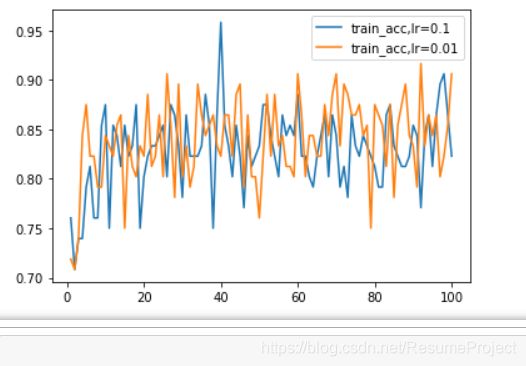
结果展示
不 同 学 习 率 下 训 练 集 的 准 确 度 对 比 不同学习率下训练集的准确度对比 不同学习率下训练集的准确度对比
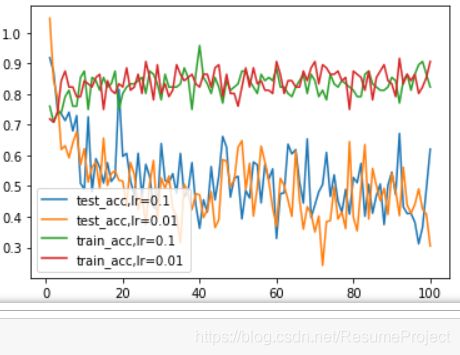
不 同 学 习 率 下 测 试 集 的 准 确 度 对 比 不同学习率下测试集的准确度对比 不同学习率下测试集的准确度对比
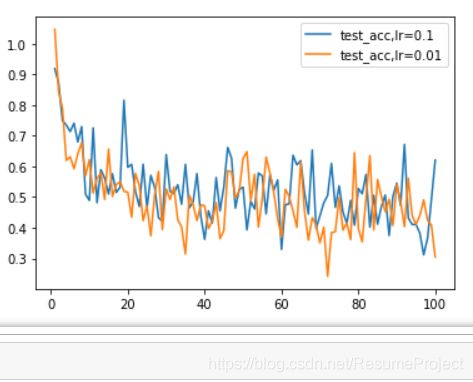
训 练 集 与 测 试 集 的 综 合 准 确 度 对 比 训练集与测试集的综合准确度对比 训练集与测试集的综合准确度对比