李宏毅机器学习day2
这里排版有点难看,等我后面有时间过来重新排版一下。
有些图片不确定能否成功粘贴过来,我把印象笔记的链接放到这里: 印象笔记day2
正文:
要自己尽量判断到底是哪些因素导致了error,然后来降低error
bias偏差
variance方差
estimator估计函数
mean平均数
variable变量
sample抽样
抽样N个点,算平均值
虽然取样N个样本算出来的mean不一定==u
但是如果N很大的话,他们的期望值是正好==u的
这里满足大数定律(个人理解)
大数定律:
概率论 历史上第一个 极限 定理属于 伯努利 ,后人称之为“大数定律”。概率论中讨论 随机变量 序列 的 算术平均值 向 随机变量 各数学期望的 算术平均值 收敛的定律。
在随机事件的大量重复出现中,往往呈现几乎 必然 的规律,这个规律就是大数定律。通俗地说,这个定理就是,在试验不变的条件下,重复试验多次,随机事件的频率近似于它的概率。偶然中包含着某种必然。
这里的larger和smaller反了,因为数量越多是越密集的,数量越少是越分散的
如果要估算variance,得儿塔的平方---方差
右边竖线上应该是s的平方而不是s,因为 这里用s的平方作为方差得儿塔的平方的估计值
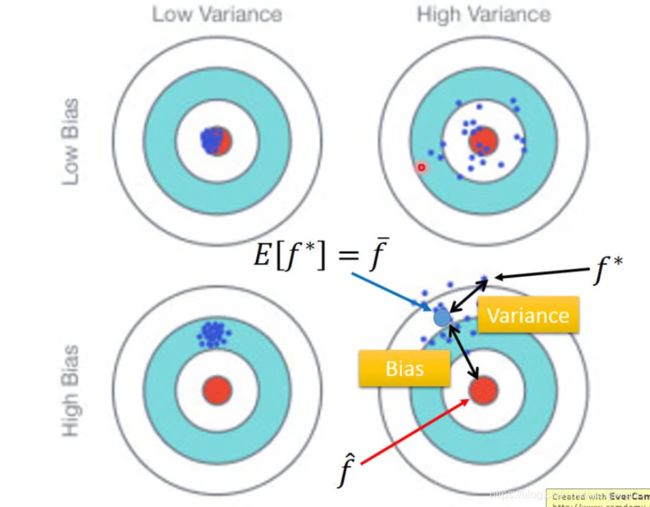
一图搞懂variance和bias
上图的E表示期望值,f横线表示平均值,f*表示很多次试验的结果。
那么实验结果和真正最优解的距离取决于两件事:
bias偏差
variance方差
在上图也可以理解为:中心点相对于靶心的平移+各点相对于中心点的扩散
bias决定了实验各点的中心点距离真正的最优解(靶心)有多远
variance决定了实验的每个点与其中心点的关系,到底是分布相对分散还是紧紧团结在中心点周围
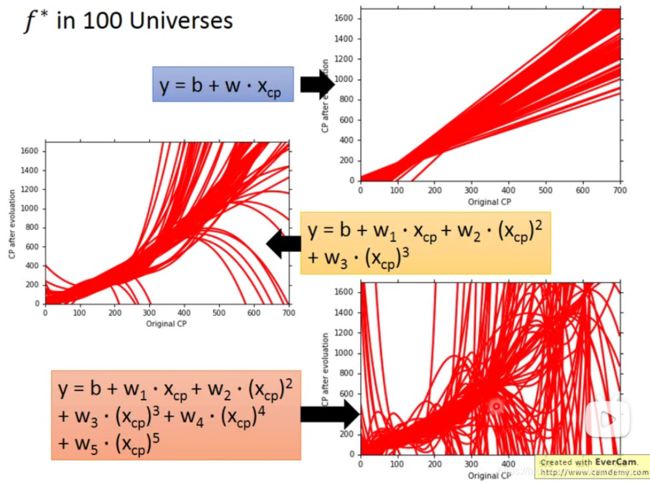
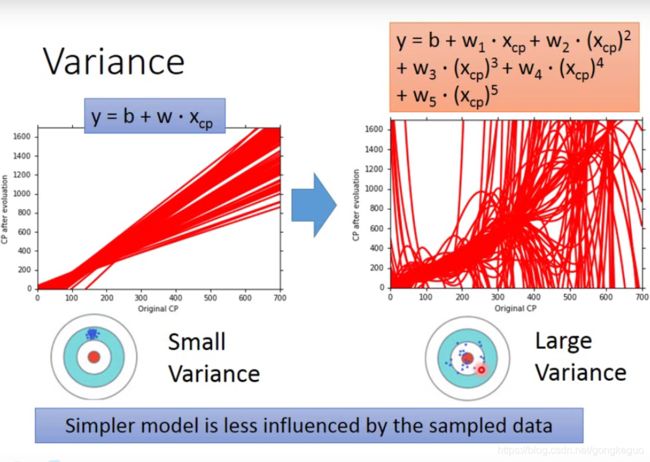
简单的model的variance比较小,分布集中,复杂的model的variance比较大,分布分散。为什么呢?
因为简单的model不容易受sampled data采样数据的影响,而复杂的model受到sampled data采样数据影响较大。这里举了一个很极端的例子:当f(x)=c,即函数式是一个常数的时候,无论你给x怎样的输入,输出也是“相当平滑”的一条直线,不可能产生较大波动。
个人理解:这里其实就是涉及到了所选模型能够达到的复杂程度范围。次幂低的是一个小圈,次幂高的是外面的一个大圈,这就类似集合和子集的关系。
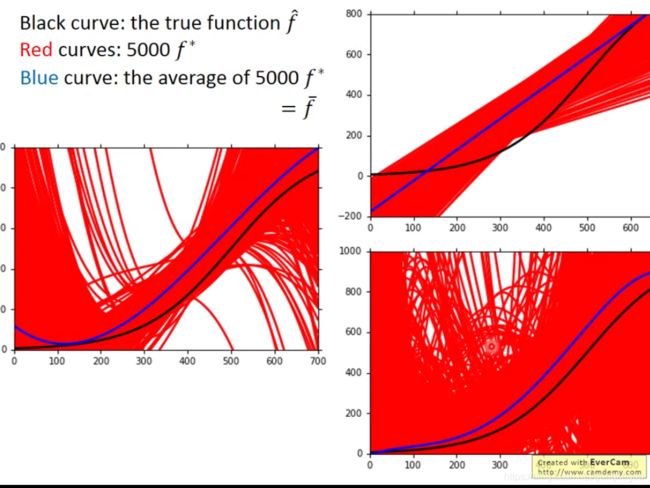
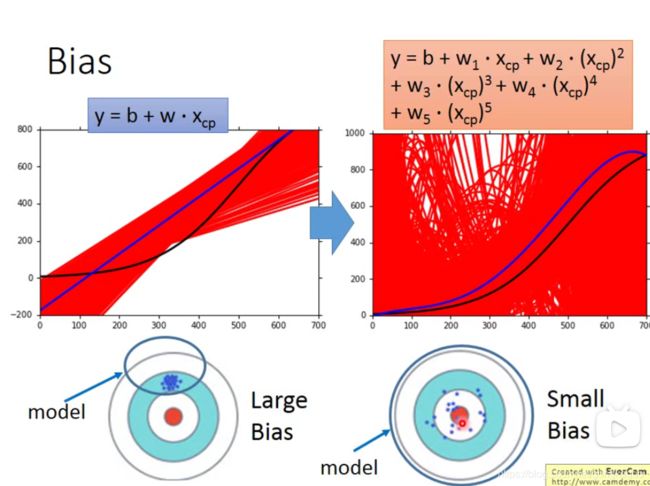
假设靶心位置是这条黑色曲线
在这里发现model越复杂,它的bias(偏差)反而越小(与之前理解的model再更加复杂error反而增大似乎不太一致)
这张图说明了这一点:model越简单,它能够考虑到的space就越小,model越复杂,space就越大。如果model太简单,根本不可能包含target区域,那么bias注定很大。如果model复杂,包含了target,就可以获得较小的bias
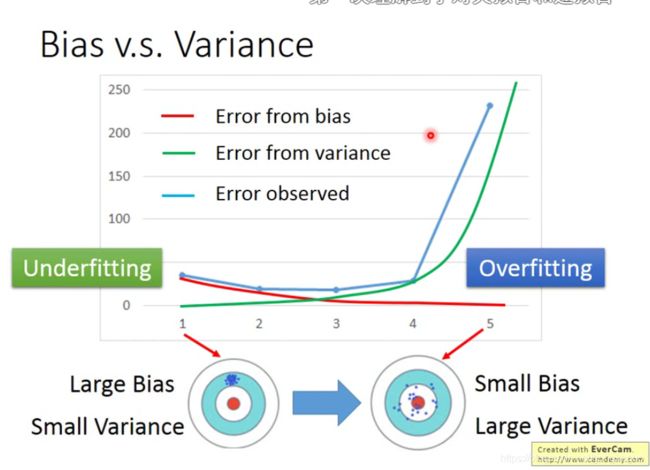
这张图很好的诠释了欠拟合和过拟合,之前看周志华的西瓜书只是心里大体知道这样的概念:
欠拟合就是对训练数据训练的太少了,导致训练出的model在训练集和测试集上都没有足够好的表现。
过拟合就是对训练数据过分追求契合了,导致model在训练集上表现得很完美,但是在测试集上表现得很离谱。
而这张图让我在原有的认识上有了进一步的领会:
欠拟合就是model太简单(浅显的说可以认为是次幂太低,当然model简单的意思不止于此),包含不了target区域,bias(偏差)太大而variance(方差)小----当然这说的是训练出来的model在测试集上的表现
过拟合就是model太复杂,space包含了target区域,平均值距离target很近,bias很小,但是variance很大。
这里相对于原有的理解,对我欠拟合和过拟合的领会引入了三个主要的概念:bias,variance,space与target的关系。为李宏毅老师精彩的讲解鼓掌!!!!(呱唧呱唧呱唧)
这里讲了当我们设计的model差强人意的时候,我们要怎么知道按照哪个方向来改进我们的model呢,到底是过拟合了呢还是欠拟合了呢?
主要是看我们训练后的model在训练集和测试集上的表现:
model不光在测试集上表现得不好,甚至在训练集上表现得也不好,大概就是欠拟合----是什么让我用了大概两个字呢,是谦虚吗,不,是对知识的敬畏(匮乏)
如果model在训练集上表现得较好,在测试集上表现得不好,大概就是过拟合了
好像搞了半天跟我原来对欠拟合过拟合的理解是一样的,不过有了一点更深入的理解终归是好事情哈哈哈
说一下改进方法:
如果是欠拟合,需要 重新design你的model:
1.考虑更多的feature作为model的输入,比如原来只考虑了皮卡丘的CP值,可以考虑尝试把它的身高体重加进去作为影响因素,看能不能得到更为满意的model
2.设计一个更加复杂的model(比如升次幂之类的)
在原来的data足够将现有model模型训练到极致的情况下,收集更多的data是没有帮助的,只能是redesign你的model。当然我感觉redesign the model的方法包括但不限于上述两条,不要限制了自己的脑洞
如果是过拟合,一般也有两个方法:
1.增加训练集中的数据。这种方法能用则用,实在因为客观条件限制收集不了更多data的时候,也可以自己造出一些看起来靠谱的data去参加训练。比如将原有图片方向翻转,男声变女声,采集多组数据合成想要的那一种数据,都ok,这样会让你多出一倍乃至几倍的训练date量,能够更好的在训练阶段规范你的model,使之对于你要测试的一类特定输入更具有普适性(非李老师原话,仅限于个人理解)
2.regularization 在loss函数中增加后面参数比重,迫使参数小下去,使得曲线变得更加平滑,平滑了variance自然也就小了。然而这种方法是月满则亏,过犹不及的,一味注重loss函数中后面一项系数的比重,也就忽视了前项的bias的重要性,既然强迫曲线变得平滑,那么就可能使得model的space没办法包含target区域,在曲线变平滑的过程中可能会导致bias的增大。所以采用这种方法的时候需要同时考虑bias和variance,使得model在这两者之间取得平衡。
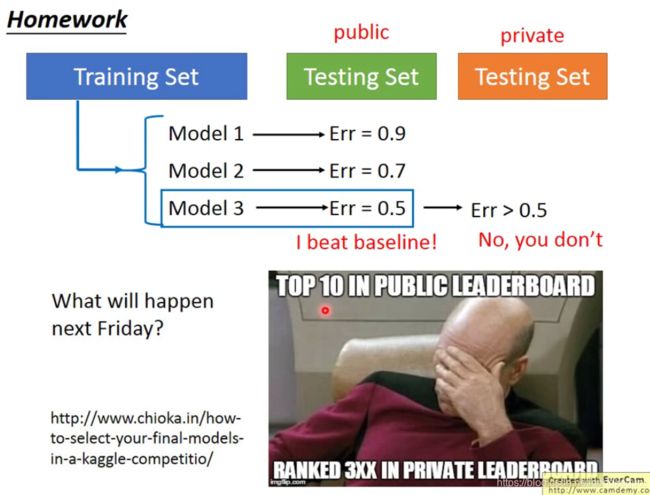
很多时候我们会面临这样的情况。我们手上有一组训练集,一组测试集。我们手头呢有三个待考虑的model。我们为了评估这三个model的好坏,于是我们将三个model分别用训练集训练,再将训练好的model用到我们的测试集上来进行评估。结果显示这三个model的error分别是0.9,0.7和0.5。于是我们认为model是最好的model。但是这里有一个问题:
我们手上的测试集并不是我们真正使用model时实际面临的测试集,也就是说我们手头的有限的已知测试集并不能很好的代表数量巨大的未知的测试集,因此我们手头测试集相对于真正测试集而言是有一个自己的bias的,因此我们采用如上方法挑选出的“最好”model,实际应用中的error很可能是大于0.5的。
numpy和panda
validation验证集
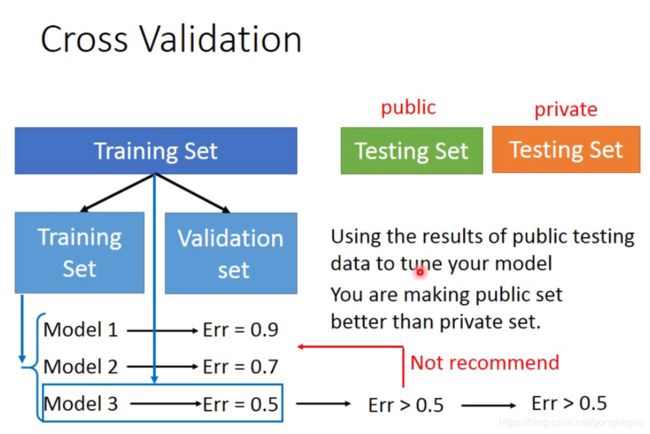
在机器学习中,一般将样本分成独立的三部分训练集(train set),验证集(validation set)和测试集(test set)。其中,测试集用来检验最终选择最优的模型的性能如何。 在 机器学习 和 模式识别 等领域中,一般需要将样本分成独立的三部分 训练集 (train set),验证集(validation set ) 和 测试集 (test set)。其中训练集用来估计模型,验证集用来确定网络结构或者控制模型复杂程度的参数,而测试集则检验最终选择最优的模型的性能如何。一个典型的划分是训练集占总样本的50%,而其它各占25%,三部分都是从样本中随机抽取。 但是,当样本总量少的时候,上面的划分就不合适了。常用的是留少部分做测试集。然后对其余N个样本采用K折交叉验证法。就是将样本打乱,然后均匀分成K份,轮流选择其中K-1份训练,剩余的一份做验证,计算预测误差平方和,最后把K次的预测误差平方和再做平均作为选择最优模型结构的依据。特别的K取N,就是留一法(leave one out)。
回到上图。这里将原来的训练集分为了新的训练集和验证集。用训练集来训练model,用验证集来评估model的好坏,然后用手头的测试集去测试model,当然这时得出的error往往比验证集的error更大,一般你会忍不住去回头调节model的结构或者参数企图在手头的测试集上取得更好的表现,但是一般不建议这么做。因为如此操作的话相当于把测试集也考虑了进去,这样会使得训练出的model在手头测试集上的表现优于在未来实际测试集中的表现,而这往往会让实际结果超出你的预期。
当然这里根据手头测试集来调节model应是情理之中的事情,不过不要希望调出来的model在未来未知测试集上的表现和手头测试集的表现一样好就是了。(个人理解)
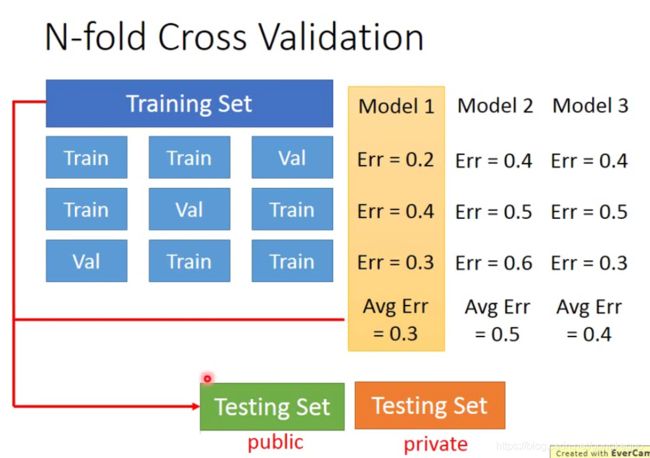
这里讲的应该就是K折交叉验证了。如果样本总量较少,可以把训练数据集分成好几份,同一时间保留一份作为验证集,其他作为训练集,交叉验证。每一次验证保留每个model的error,所有验证结束后,计算每个model的平均error,以此为根据挑选出最佳model。