深度优先搜索dfs剪枝例题讲解

引爆炸弹
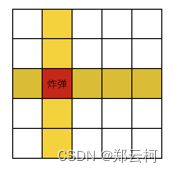
在一个 n×m 的方格地图上，某些方格上放置着炸弹。手动引爆一个炸弹以后，炸弹会把炸弹所在的行和列上的所有炸弹引爆，被引爆的炸弹又能引爆其他炸弹，这样连锁下去。

现在为了引爆地图上的所有炸弹，需要手动引爆其中一些炸弹，为了把危险程度降到最低，请算出最少手动引爆多少个炸弹可以把地图上的所有炸弹引爆。
数据范围：1≤n,m≤1000；

这问题其实与连通块类似。
我们把可以互相引爆的炸弹放到同一个集合中，那么最后划分的集合个数就是我们要求的答案。显然，引爆集合中任意一个炸弹造成的效果都一样，我们可以遍历nm的方格中所有炸弹，如果当前炸弹之前没被引爆，就引爆它，即标记他所在集合中的所有炸弹。
可以用DFS搜出一个炸弹所在的集合，每次引爆一个炸弹后，就搜它所在的行列是否有其他炸弹，然后继续搜索。因为每次炸弹最多有nm个，每个炸弹引爆后要检查所在行和列都有没有炸弹，时间复杂度是O(nm(n+m))
这里有一个剪枝，每行每列最多搜一遍，于是可以标记一下搜过的行列避免重复搜索，这样每个格子都最多被检查两边，时间复杂度为O(nm)

row和col分别表示每行、列是否考虑过引爆。
boom函数，首先标记当前炸弹已经被引爆。如果当前行没有被引爆，就应该循环判断该行是否有没有引爆的炸弹并引爆。
如果当前列没有引爆过，那就引爆当前列并标记，然后循环判断该列是否有没有引爆的炸弹，有就继续搜索。
在main函数里，我们要统计答案，只要遍历n*m的方格，每遇到一个没引爆的炸弹，答案就增加1，并调用boom函数引爆所有相关联的炸弹。
示例代码：

#include 
#include 
using namespace std;
char mat[1010][1010];
int n, m;
bool row[1010],col[1010];
void boom(int x,int y){
    mat[x][y]=0;
    if(!row[x]){
        row[x]=true;
        for(int i=0;i<m;i++){
            if(mat[x][i]=='1'){
                boom(x,i);
            }
        }
    }
    if(!col[y]){
        col[y]=true;
        for(int i=0;i<n;i++){
            if(mat[i][y]=='1'){
                boom(i,y);
            }
        }
    }
}
int main() {
    cin >> n >> m;
    for (int i = 0; i < n; ++i) {
        scanf("%s", mat[i]);
    }
    int cnt=0;
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            if(mat[i][j]=='1'){
                cnt++; 
                boom(i,j);
            }
        }
    }
    cout<<cnt<<endl;
    return 0;
}

生日蛋糕
今天是花椰妹的生日，蒜头君打算制作一个体积为 nπ 的 m 层生日蛋糕送给她。蛋糕每层都是一个圆柱体，设从下往上数第 i(0≤i0 时，要求R[i] 由于要在蛋糕上抹奶油，为尽可能节约经费，我们希望蛋糕外表面（最下一层的下底面除外）的面积 Q 最小。令iQ=Sπ，请编程对给出的 n 和 m，找出蛋糕的制作方案（适当的 R[i]和H[i] 的值），使 S 最小。（除 Q 外，以上所有数据皆为正整数）

为了方便叙述，本体表面积和体积是除以pai以后的结果，且表面积是指除去下底面后的表面积。
整个蛋糕的体积$$n=\sum _{i=0}^{m-1}{R}_i^2{H}_i$$
表面积$$s=R_0^2+2\sum _{i=0}^{m-1}{R}_i{H}_i$$
因为每个圆柱体的半径和高都是正整数，所以不能用数学方法直接求出最值，只能通过DFS搜索的办法寻找答案。
容易发现，除了第0层以外，在体积一定的情况下$R_i$越大，表面积越小。这样我们在搜索过程中，会从大到小枚举$R_i$，更有利于之后的剪枝优化。

现在我们来考虑第i层时，$R_i$和$H_i$的枚举范围。
题目要求$R_i<R_{i-1}$,而$R_i$必须是正整数，那么因为$R_{m-1}\ge 1$,可以推出$R_i\ge m-i$
因此当i>0时，$R_i\in \left[m-i,R_{i-1}-1\right]$同理，$H_i\in \left[m-i,H_{i-1}-1\right]$。最底层$R_0\le \sqrt{n},H_0\le n$。
这样，我们就对每层枚举都做了剪枝。

有些时候，当前情况体积太大，导致即使后面几层体积取到最小，也无法使最终体积等于n。
我们开一个数组va预处理从上往下前i个圆柱最小的体积和，显然$va[i]={\sum }_{j=1}^i{j}^3$。那么在我们搜索中，就可以利用这个va数组进行可行性剪枝。

下面我们考虑最优性剪枝，如果已经搜到了一个答案ans，而当前表面积为s，当前体积为v，若$s+x\le ans$，就能进行剪枝。
其中x是第i层到第m-1层的最小表面积，我们在没搜索之前是无法计算出这个x的，但是能根据当前局面估计出一个值y，满足$y\le x$。我们在$s+y\le ans$时进行剪枝，显然y越接近x，剪枝效果越好。
下面我们通过不等式的放缩来找到这个y。
当前在第i层，因为
$x=2{\sum }_{j-i}^{m-1}{R}_j{H}_j$

$x=\frac{2}{R_i}.{\sum }_{j=i}^{m-1}{R}_i{R}_j{H}_j$

$R_i\ge R_j$

$x\le \frac{2}{R_i}{\sum }_{j=i}^{m-1}{R}_j^2{H}_j$

$x\le \frac{2(n-v)}{R_i}=y$
这样，我们只需要在$s+\frac{2(n-v)}{R_i}\ge ans$

示例代码：

#include 
#include 
#include 
#include 
using namespace std;
const int INF = 0x3f3f3f3f;
int n, m;
int ans;
int va[20];
void dfs(int u,int v,int s,int r0,int h0){
    if(u==m){
        if(v==n){
            ans=min(ans,s);
        }
        return;
    }
    if(va[m-u]+v>n)
        return;
    if(2.0*(n-v)/r0+s>ans)
        return;
    for(int r=r0;r>=m-u;r--){
        for(int h=h0;h>=m-u;h--){
            int tv=v+r*r*h;
            if(tv>n)
                continue;
            int ts=s+2*r*h;
            if(u==0)
                ts+=r*r;
            dfs(u+1,tv,ts,r-1,h-1);
        }
    }
}
int main() {
    cin >> n >> m;
    for(int i=1;i<=m;i++){
        va[i]=va[i-1]+i*i*i;
    }
    int r0=sqrt(n)+0.5;
    ans=INF;
    dfs(0,0,0,r0,n);
    if(ans==INF)
        ans=0;
    cout<<ans<<endl;
    return 0;
}