Neuronal Dynamics:Two dimensions model 实验结果展示
Neuronal Dynamics:Two dimensions model 实验结果展示
- 一、演示效果和代码
- 二、模型简述
-
- 2.1 Morris-Lecar model
- 2.2 FitzHugh-Nagumo model
- 三、输出解释
-
- 3.1 Morris-Lecar model
- 3.2 FitzHugh-Nagumo model
一、演示效果和代码
本次实验以Morris-Lecar model 和 FitzHugh-Nagumo model两种模型为例研究了模型w,u随t变化的图像。
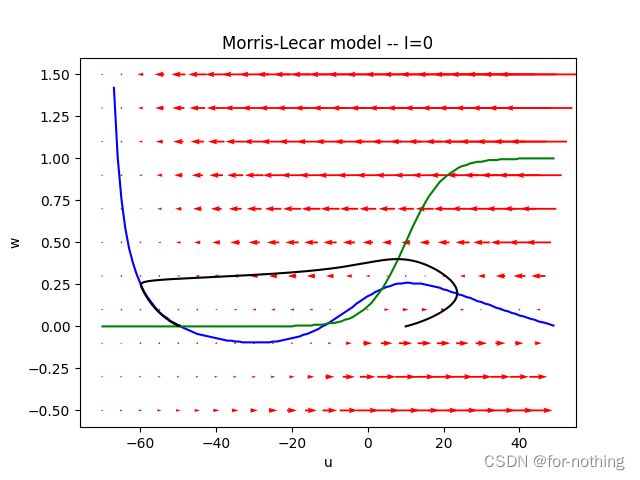
输出结果如下(蓝色线为 d u d t = 0 \frac{du}{dt}=0 dtdu=0,绿色线为 d w d t = 0 \frac{dw}{dt}=0 dtdw=0,黑色的线为(u,w)随时间t的变化轨迹曲线):



代码如下:
import numpy as np
import matplotlib.pyplot as plt
class two_dimensions_model():
#type=0 is Morris-Lecar model
#type=1 is FitzHugh-Nagumo model
def __init__(self):
self.C=20
self.Vl=-50
self.V1=100
self.V2=-70
self.gl=2
self.g1=4
self.g2=8
self.u1=0
self.u2=15
self.u3=10
self.u4=10
self.tw=0.1
self.type=0
self.b0=0
self.b1=1
self.I=0
def m0u(self,u):
return (1+np.tanh((u-self.u1)/self.u2))/2
def w0u(self,u):
return (1+np.tanh((u-self.u3)/self.u4))/2
def tu(self,u):
return self.tw/np.cosh((u-self.u3)/2/self.u4)
def dudt(self,u,w):
if self.type==0:
return 1/self.C*(-self.g1*self.m0u(u)*(u-self.V1)-self.g2*w*(u-self.V2)-self.gl*(u-self.Vl)+self.I)
elif self.type==1:
return u-u*u*u/3-w+self.I
def dwdt(self,u,w):
if self.type==0:
return -(w-self.w0u(u))*self.tu(u)
else:
return self.b0+self.b1*u-w
def plot_u_w_0_line(self,a,b,max_dif=0.1):
x, y = np.meshgrid(a, b)
x = x.T
y = y.T
imax = len(x)
jmax = len(x[0])
u = [[0 for j in range(jmax)] for i in range(imax)]
w = [[0 for j in range(jmax)] for i in range(imax)]
for i in range(imax):
for j in range(jmax):
i0 = x[i][j]
j0 = y[i][j]
u[i][j] = self.dudt(i0, j0)
w[i][j] = self.dwdt(i0, j0)
u1 = []
w1 = []
u2 = []
w2 = []
for i in range(imax):
minu = np.min(np.abs(u[i]))
minw = np.min(np.abs(w[i]))
if minu < max_dif:
j = np.where(minu == np.abs(u[i]))
u1.append(x[i][j])
w1.append(y[i][j])
if minw < max_dif:
j = np.where(minw == np.abs(w[i]))
u2.append(x[i][j])
w2.append(y[i][j])
plt.plot(u1, w1, color="b")
plt.plot(u2, w2, color="g")
def plot_vector(self, a, b):
x, y = np.meshgrid(a, b)
x = x.T
y = y.T
imax = len(x)
jmax = len(x[0])
u = [[0 for j in range(jmax)] for i in range(imax)]
w = [[0 for j in range(jmax)] for i in range(imax)]
for i in range(imax):
for j in range(jmax):
i0 = x[i][j]
j0 = y[i][j]
u[i][j] = self.dudt(i0, j0)
w[i][j] = self.dwdt(i0, j0)
plt.quiver(x,y,u,w,color="r",pivot="mid")
def plot_trace(self,a,b,x0,y0,time=1000,dt=0.1):
x, y = np.meshgrid(a, b)
x = x.T
y = y.T
imax = len(x)
jmax = len(x[0])
u = [[0 for j in range(jmax)] for i in range(imax)]
w = [[0 for j in range(jmax)] for i in range(imax)]
for i in range(imax):
for j in range(jmax):
i0 = x[i][j]
j0 = y[i][j]
u[i][j] = self.dudt(i0, j0)
w[i][j] = self.dwdt(i0, j0)
u0 = []
w0 = []
tmp = np.array([i[0] for i in x])
for k in range(int(time/dt)):
u0.append(x0)
w0.append(y0)
minu = np.min(np.abs(tmp-x0))
i = np.where(minu == np.abs(tmp-x0))[0][0]
minw = np.min(np.abs(y[0]-y0))
j = np.where(minw == np.abs(y[0]-y0))[0][0]
x0 = x0+u[i][j]*dt
y0 = y0+w[i][j]*dt
# print(x0,y0,u[i][j],w[i][j])
plt.plot(u0, w0,c='k')
if __name__ == '__main__':
model = two_dimensions_model()
# 1.1 type== 0 Morris-Lecar model-1 (I=0)
model.type=0
model.I = 0
a = np.arange(-70, 50, 1)
b = np.arange(-0.5, 1.5, 0.005)
model.plot_u_w_0_line(a,b)
a = np.arange(-70, 50, 5)
b = np.arange(-0.5, 1.51, 0.2)
model.plot_vector(a,b)
a = np.arange(-70, 50, 0.1)
b = np.arange(-0.5, 1.5, 0.01)
model.plot_trace(a, b, 10,0,time=1000,dt=0.1)
plt.title('Morris-Lecar model -- I=0')
plt.xlabel('u')
plt.ylabel('w')
plt.savefig('Morris_Lecar_model_I=0.png')
plt.show()
plt.cla()
#1.2 type== 0 Morris-Lecar model-1 (I=50)
model.type = 0
model.I = 50
a = np.arange(-70, 50, 1)
b = np.arange(-0.5, 1.5, 0.005)
model.plot_u_w_0_line(a, b)
a = np.arange(-70, 50, 5)
b = np.arange(-0.5, 1.51, 0.2)
model.plot_vector(a, b)
a = np.arange(-70, 50, 0.1)
b = np.arange(-0.5, 1.5, 0.01)
model.plot_trace(a, b, 10, 0, time=1000, dt=0.1)
plt.title('Morris-Lecar model -- I=50')
plt.xlabel('u')
plt.ylabel('w')
plt.savefig('Morris_Lecar_model_I=50.png')
plt.show()
plt.cla()
# 2.1 type==1 FitzHugh0Nagumo model I=0,b1<1,b0=0
model.type = 1
model.b0 = 0
model.b1 = 0.5
model.I = 0
a = np.arange(-2, 2, 0.1)
b = np.arange(-1, 1.5, 0.01)
model.plot_u_w_0_line(a, b)
a = np.arange(-2, 2, 0.1)
b = np.arange(-1, 1.51, 0.2)
model.plot_vector(a, b)
a = np.arange(-2, 2, 0.01)
b = np.arange(-1, 1.5, 0.01)
model.plot_trace(a, b, -0.5, -0.3, time=10000, dt=0.1)
model.plot_trace(a, b, 0.5, -0.3, time=10000, dt=0.1)
plt.title('FitzHugh-Nagumo model -- I=0,b1<1,b0=0')
plt.xlabel('u')
plt.ylabel('w')
plt.savefig('FitzHugh_Nagumo_model_I=0_b1_smaller_1_b0_0.png')
plt.show()
plt.cla()
# 2.2 type==1 FitzHugh0Nagumo model I=0.5,b1<1,b0=0
model.type = 1
model.b0 = 0
model.b1 = 0.5
model.I=0.5
a = np.arange(-2, 2, 0.1)
b = np.arange(-1, 1.5, 0.01)
model.plot_u_w_0_line(a, b)
a = np.arange(-2, 2, 0.1)
b = np.arange(-1, 1.51, 0.2)
model.plot_vector(a, b)
a = np.arange(-2, 2, 0.01)
b = np.arange(-1, 1.5, 0.01)
model.plot_trace(a, b, -0.5, -0.3, time=10000, dt=0.1)
model.plot_trace(a, b, 0.5, -0.3, time=10000, dt=0.1)
plt.title('FitzHugh-Nagumo model -- I=0.5,b1<1,b0=0')
plt.xlabel('u')
plt.ylabel('w')
plt.savefig('FitzHugh_Nagumo_model_I=0_5_b1_smaller_1_b0_0.png')
plt.show()
plt.cla()
#3.1 type==1 FitzHugh0Nagumo model I=0,b1>1,b0=1
model.type=1
model.b0 = 1
model.b1 = 1.2
model.I = 0
a = np.arange(-2, 2, 0.1)
b = np.arange(-1.5, 1.5, 0.01)
model.plot_u_w_0_line(a,b)
a = np.arange(-2, 2, 0.1)
b = np.arange(-1.5, 1.51, 0.2)
model.plot_vector(a,b)
a = np.arange(-2, 2, 0.1)
b = np.arange(-1.5, 1.5, 0.01)
model.plot_trace(a, b, 0.5, -0.3,time=10000,dt=0.1)
plt.title('FitzHugh-Nagumo model -- I=0,b1>1,b0=1')
plt.xlabel('u')
plt.ylabel('w')
plt.savefig('FitzHugh_Nagumo_model_I=0_b1_bigger_1_b0_1.png')
plt.show()
#3.2. type==1 FitzHugh0Nagumo model I=1,b1>1,b0=0
model.type = 1
model.b0 = 1
model.b1 = 1.2
model.I = 1
a = np.arange(-2, 2, 0.1)
b = np.arange(-0.5, 3, 0.01)
model.plot_u_w_0_line(a, b)
a = np.arange(-2, 2, 0.1)
b = np.arange(-0.5, 3.1, 0.2)
model.plot_vector(a, b)
a = np.arange(-2, 2, 0.1)
b = np.arange(-0.5, 3.1, 0.2)
model.plot_trace(a, b, -0.5, -0.3)
plt.title('FitzHugh-Nagumo model -- I=1,b1>1,b0=1')
plt.xlabel('u')
plt.ylabel('w')
plt.savefig('FitzHugh_Nagumo_model_I=1_b1_bigger_1_b0_1.png')
plt.show()
二、模型简述
2.1 Morris-Lecar model
模型包含下列两个微分方程:
C d u d t = − g 1 m ^ 0 ( u ) ( u − V 1 ) − g 2 w ^ ( u − V 2 ) − g L ( u − V L ) + I ( t ) C\frac{du}{dt}=-g_1\hat{m}_0(u)(u-V_1)-g_2\hat{w}(u-V_2)-g_L(u-V_L)+I(t) Cdtdu=−g1m^0(u)(u−V1)−g2w^(u−V2)−gL(u−VL)+I(t) d w ^ d t = − 1 τ ( u ) [ w ^ − w 0 ( u ) ] \frac{d\hat w}{dt}=-\frac1{\tau(u)}[\hat w-w_0(u)] dtdw^=−τ(u)1[w^−w0(u)]
其中
m ^ 0 ( u ) = 1 2 [ 1 + t a n h ( u − u 1 u 2 ) ] \hat m_0(u)=\frac{1}{2}[1+tanh(\frac{u-u_1}{u_2})] m^0(u)=21[1+tanh(u2u−u1)]
w 0 ( u ) = 1 2 [ 1 + t a n h ( u − u 3 u 4 ) ] w_0(u)=\frac12[1+tanh(\frac{u-u_3}{u_4})] w0(u)=21[1+tanh(u4u−u3)]
τ 0 ( u ) = τ w c o s h ( u − u 3 2 u 4 ) \tau_0(u)=\frac{\tau_w}{cosh(\frac{u-u_3}{2u_4})} τ0(u)=cosh(2u4u−u3)τw
模型使用的参数为:
C=20,V1=100,V2=-70,VL=-50,g1=4,g2=8,gL2
u1=0,u2=15,u3=10,u4=10,tw=0.1
疑惑:书上写的是 m ^ 0 ( u ) = [ m 0 ( u ) ] 3 , 然后 m 0 ( u ) = 1 2 [ 1 + t a n h ( u − u 1 u 2 ) ] \hat m_0(u)=[m_0(u)]^3,然后m_0(u)=\frac{1}{2}[1+tanh(\frac{u-u_1}{u_2})] m^0(u)=[m0(u)]3,然后m0(u)=21[1+tanh(u2u−u1)],与我现在使用的略有不同
从网络上查找的模型和实验带入参数来看,上述的模型感觉比书上的更合理,不知道是不是书上这一块写的有问题
2.2 FitzHugh-Nagumo model
模型包含以下两个微分方程:
τ d u d t = u − 1 3 u 3 − w + I \tau\frac{du}{dt}=u-\frac13u^3-w+I τdtdu=u−31u3−w+I τ w d w d t = b 0 + b 1 u − w \tau_w\frac{dw}{dt}=b_0+b_1u-w τwdtdw=b0+b1u−w
在实际代码实现中我令 τ = τ w = 1 \tau=\tau_w=1 τ=τw=1,改变b0和b1的值进行讨论
三、输出解释
3.1 Morris-Lecar model


图中蓝色线为 d u d t = 0 \frac{du}{dt}=0 dtdu=0,绿色线为 d w d t = 0 \frac{dw}{dt}=0 dtdw=0,黑色的线为(u,w)随时间t的变化轨迹曲线
在外部输入I=0的时候,从随机取得一个点开始,电压u的值先增大然后减小缓缓恢复到稳定点
在外部有持续输入I=50的时候,从随机取得一个点开始,此时电压并不会回到一个固定点,此时稳定点已经不存在,(w,u)的值会在一段时间后开始沿着一定的轨迹不断往复循环,即u产生振荡
3.2 FitzHugh-Nagumo model


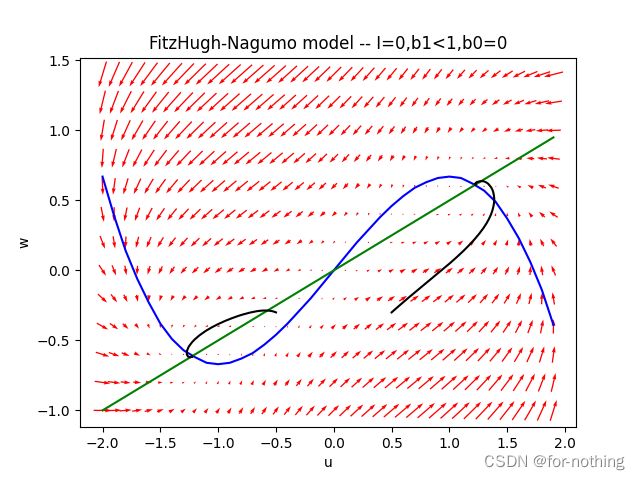
图中蓝色线为 d u d t = 0 \frac{du}{dt}=0 dtdu=0,绿色线为 d w d t = 0 \frac{dw}{dt}=0 dtdw=0,黑色的线为(u,w)随时间t的变化轨迹曲线
此时我们取模型中的b0=0,b1=0.5<1
左图为输入电流I等于0的时候,此时有左右各一个稳定点中间一个鞍点,我们从随机的两个点出发发现他们最后分别停留在两个不同的稳定点
右图为输入电流I=0.5的时候,我们再从刚刚两个随件点出发,此时左边的稳定点和鞍点已经合并并且消失,然后由于右边的还是一个稳定点而不是不稳定点,所以并不会产生振荡。


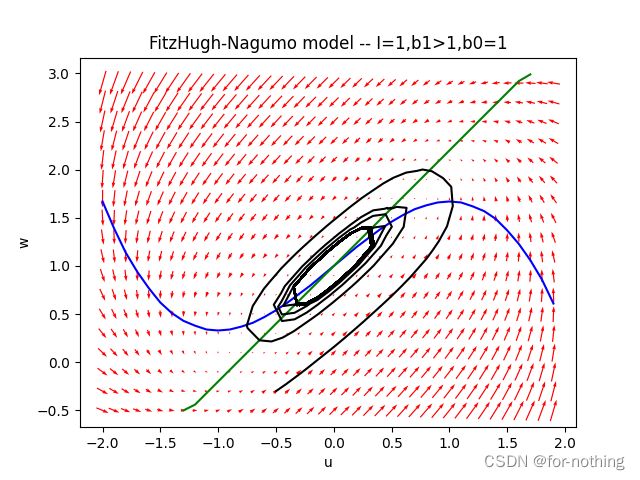
图中蓝色线为 d u d t = 0 \frac{du}{dt}=0 dtdu=0,绿色线为 d w d t = 0 \frac{dw}{dt}=0 dtdw=0,黑色的线为(u,w)随时间t的变化轨迹曲线
此时我们取模型中的b0=1,b1=1.2>1
由于b1>1,所以 d u d t = 0 \frac{du}{dt}=0 dtdu=0与 d w d t = 0 \frac{dw}{dt}=0 dtdw=0只有一个交叉点
左图为输入电流I=0的时候,从随机一个点出发我们可以看到它最后停止在了交叉点,说明此时交叉点为稳定点
右图为输入电流I=1的时候,从随机一个点出发我们可以看到它并没有停止在交叉点,而是沿着一个轨迹不断循环,说明此时交叉点已经由稳定点变为不稳定点,电压u在不断振荡。