数字图像处理- 3.6 锐化空间滤波器

3.6 锐化空间滤波器

锐化处理的主要目的是突出图像中的突出灰度的过度部分。总的来说，微分算子的响应强度与图像在该店(应用了算子)的突变程度有关。这样一来，图像微分增强了边缘和其他突变(如噪声)并削弱了灰度变化缓慢的区域。

 为了说明简单，主要集中讨论一阶微分的性质。我们最高兴去的微分性质是恒定灰度区域(平坦段)、突变的开头与结尾(阶梯和斜坡突变)及沿着灰度级斜坡处的特性。这些类型的突变可以用来对图像中的噪声点、细线与边缘模型化。

3.6.1 基础

数字函数（图像，离散的数字序列）的微分定义条件：

  这里我们首先了解下数学函数的微分，微分可以用不同的术语定义，也有各种方法定义这些差别，然而，对于一阶微分任何定义都必须保证以下几点：

(1)在平坦段(灰度不变区域)微分值为零；

(2)在灰度阶梯或斜坡的起始点处微分值非零；

(3)沿着斜坡面微分值非零。

任何二阶微分的定义也类似：

（1）在平坦去微分值必为零；

（2）在灰度阶梯或斜坡的起始点处微分值非零；

（3）沿着斜坡面微分值非零。

  因为我们处理的是数字量，其值是有限的，故最大灰度级的变换也是有限的，变化发生最短距离是在两相邻像素之间。

对于一元函数f(x)表达一阶微分定义是一个差值：

∂f/∂x = f(x+1) − f(x)

二阶导数：(∂f/∂x)/∂x = f(x+2) - f(x+1) -f(x+1)+f(x)

相当于：f(x+1)-2f(x)+f(x-1)

这里，为了与对二元图像函数f(x,y)求微分时的表达式保持一致，使用偏导数符号，对二元函数，我们将沿着两个空间轴处理偏微分，类似地，用差分定义二阶微分：

下图表明了上述的具体含义。

注意下图中二阶差分的零交叉点（Zero crossing），零交叉点对于边缘的定位非常有用。

由于图像边缘处的一阶微分是极值点, 图像边缘处的二阶微分应为零,确定零点的位置要比确定极值点更容易,也更准确"

我们发现交叉点就是边缘，而一阶微分中却没有这样的性质

二阶微分在增强细节方面比一阶微分好得多，这是一个适合锐化图像的理想特征。

3.6.2 基于二阶微分的图像增强--拉普拉斯算子

  这里介绍二阶微分在图像增强处理中的应用。

首先定义一个二阶微分的离散公式，然后构造一个基于此式的滤波器。

我们最关注的是一种各向同性滤波器，这种滤波器的响应与滤波器作用的图像的突变方向无关。

也就是说，各向同性滤波器是旋转不变的，即将原始图像旋转后进行滤波处理给出的结果与先对图像滤波，然后再旋转的结果相同。

   处理方法

   最简单的各向同性微分算子是拉普拉斯算子，一个二元图像函数f(x,y)的拉普拉斯变换定义为：

                                                  

因为任意阶微分都是线型操作，所以拉普拉斯变换也是一个线性操作。

考虑到有两个变量，因此，我们在x，y方向上对二阶偏微分采用下俩定义：

                                                   

                                                

因此二维拉维拉斯数字实现可由这两个分量相加得到：

                                                ，

这里关注系数矩阵即掩膜：

这个矩阵给出了在90度方向上旋转的各向同性结果，如果向得到45度方向上旋转的各向同性结果则，将中心对角点标为1，中心点为-8即可。

   由于拉普拉斯是一种微分算子，它的应用强调图像中灰度的突变及降低灰度慢变化的区域。将原始图像和拉普拉斯图像叠加在一起的简单方法可以保护拉普拉斯锐化处理的效果，同时又能复原背景信息。我们使用拉普拉斯变换对图像增强的基本方法可表示为下式：

                                                          

含有对角线信息的拉普拉斯算子

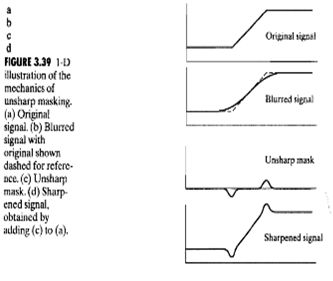
3.6.3 非锐化掩蔽和高提升滤波

在印刷和出版界用了多年的图像锐化处理过程，从原图中减去一副非锐化（平滑后的）图像，达到锐化的目的。

步骤有以下几步：

1. 模糊源图像
2. 从原图像中减去模糊图像（产生的差值图像称为模板）
3. 将模板加到原图像上。

令 表示模糊图像，那么首先我们得到模板：

然后在原图像上加上该模板的一个权重部分：

上式中，当k=1时，我们得到上面定义的非锐化掩蔽，当k>1时，该处理称为高提升滤波，当k<1时，则不强调非锐化模板的贡献。

需要注意的是，如果k足够大的时候，负值将导致边缘周围有暗的晕轮，会产生不好的效果。

3.6.4 使用一阶微分对（非线性）图像锐化—梯度

一个函数f在f(x,y)的梯度是定义为二维列向量（这是一个矢量，给定了一个方向）：

然后其幅度值为，其中M(x,y)是与原图像大小相同的图像，该图像通常称为梯度图像。后面的表达式仍保留了灰度的变换，但丢失掉了其各向同性。

下面介绍两种算子：一阶Roberts交叉梯度算子和二阶Soble算子：

在3×3的区域图像中，应该是gx = (z8−z5) gy = (z9−z6),但是Roberts进行了改良，提出了Roberts算子，gx=(z9−z5)，gy=(z8−z6)；

由于偶数模板没有对称中心，所以与之前的卷积模板定义中，运算结果等会中心点位置值不能对应， 所以使用奇数的模板，例如3 * 3 的Soble算子，gx=(z7+2z8+z9)−(z1+2z2+z3)，gy=(z3+2z6+z9)−(z1+2z4+z7)。

使用梯度进行边缘增强，可以用以突出灰度图像中看不见的小斑点，在下面的例子中甚至可以去除灰度不变或变换缓慢的图案阴影。

3.7 混合空间增强法

本书所提供例子的策略是：用Laplace突出图像中的小细节，然后使用梯度法突出边缘。

平滑过得梯度图像用于掩蔽Laplace图像，最后使用灰度变换来增大图像的灰度动态范围。

其中降低噪声可以使用中值滤波器或者使用原图像梯度操作的平滑形式形成的一个模板。

图像请直接参考Digital Image Processing （3rd Edition）Page 192。

3.8 使用模糊技术进行灰度变换和空间变换

3.8.1 引言

隶属度函数μ(z)：用以描述一个元素是否属于集合的模糊程度，若是一个阶跃函数，可以认为是一个我们所了解的"干脆的"集合，若是一个分段函数，则可以看做一个模糊集合：

3.8.2模糊集合论原理

模糊集合是一个有z值和（赋予z成员等级的）相应隶属度函数组成的序对，即

A={z,μA(z)|z∈Z}

其中隶属度函数是关键，表明了元素z到集合的一种对应关系。

如果隶属度函数仅有0,1两个值，那么模糊集合退化为"干脆的"集合。

下面这张图展示了模糊集合间的一些关系：

有一些常用的隶属度函数，如三角形、梯形、∑型、S型、种型、截尾高斯型等，之后用到了会另作介绍。

3.8.3 模糊集合的应用（略）

3.8.4 使用模糊集合进行灰度变换

对于一副灰度图像，描述它的某个区域"暗的"、"灰的"、"亮的"都是利用模糊的概念，那么我们将给予这三种情况定义三种模糊集合：

那么对于任何输入z0，输出v0为

从书中给予的例子中来看，图像的细节部分得到了比较好的保留，但代价是计算量大大增加。

写在最后：既然是为了达到锐化的目的，就是保留图像固有的边缘特性,那么在图像还原（插值）的操作中，这些滤波器仍然可以使用。而且能够保持原有图像的边缘特点。

1，直接使用可以保留边缘特性的mask进行插值。

2.利用锐化用使用的边缘检测算法对边缘求解，然后分别处理边缘区域 和 非边缘区域。