机器学习和深度学习基本概念(李宏毅)
基本概念
三个概念
1、Regression 回归 输出一个数值,通过一些基本的数值找输出数值所对应的函数就是regression
2、Classfication 分类 我们先准备好一些选项,这些选项叫类别,不一定只有一个选项,比如说alpha go就有多个选项
3、structured learning 创造和structure有关的东西
找函数的三个过程
1、写出一个带有未知参数的函数,进行一个初步的猜测,y=wx+b,wb是未知参数,带有参数的方程就叫做model,已经知道的东西x叫做feature,w叫做weight, b叫做bias
2、定义一个东西叫做loss,loss是一个function,这个function的输入就是w和b,L(b,w),输出的值代表这组参数设置值的质量的好坏,从训练资料来计算loss,用过去的数据来计算loss,把过去的数据带入y=wx+b函数,将真实的值减去方程式预测值的误差的绝对值(e)提取出来,提取出来的绝对值进行加和然后取平均值,就是Loss。当然e有多种计算方式:MAE是y-yhat的绝对值、MSE是y-yhat的平方
3、找一个最佳化optimization,即找w和b,这个课程里面用到的方法就是梯度下降(gradient descent),第一步先随机找一个w0的点,计算L对于w在w0处的微分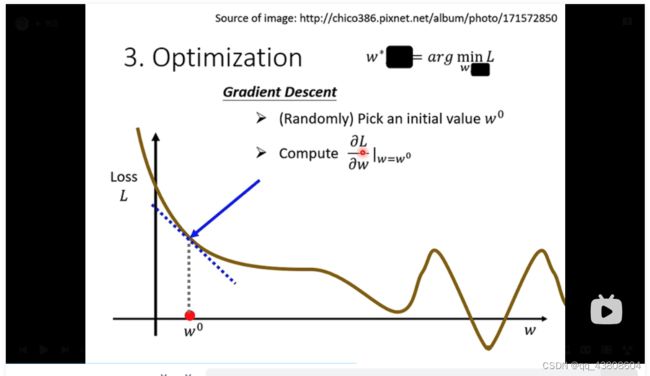
如果切线处左边比较高,右边比较低的话,就把w的值变大,就可以让loss变小。如果算出来的斜率是正的,就把w的值变小,就可以让loss变小。
向左或者向右改变w的大小的步伐大小的确定,里面包含的n叫做学习速率大小,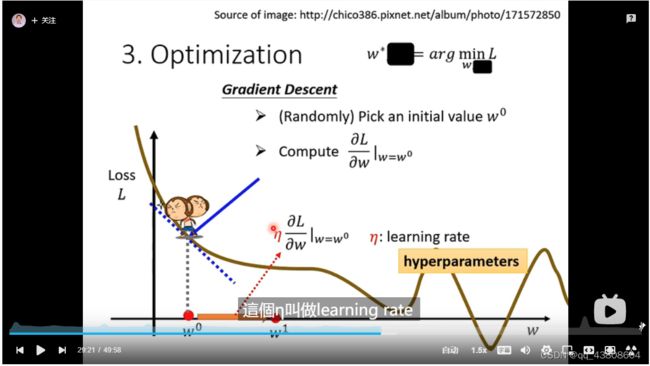
梯度下降没有真正的global minima,loss的全局最小点是一个伪命题。
然而原始的式子中有两个参数,一个w和一个b
反复同样的步骤,一直更新w和b,n是学习率,称learning rate
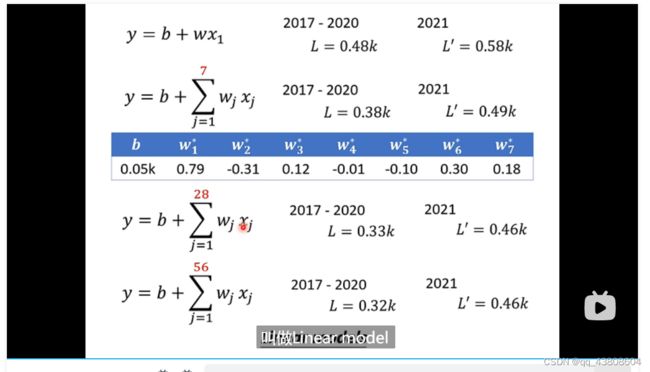
wj是前j天的参数,是一种改进,不再只关注于前一天的数据,这些实现的式子叫linear model
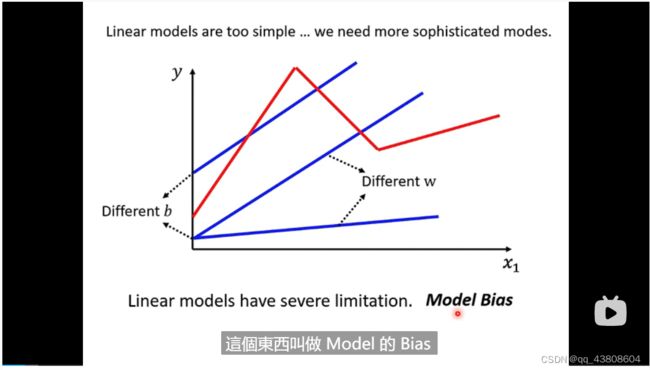
用linear model我们永远无法准确计算出红色的直线,误差叫做model bias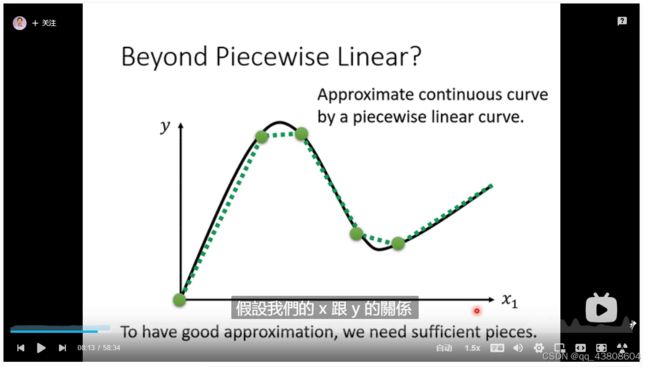
把多个function加起来就是piecewise linear curve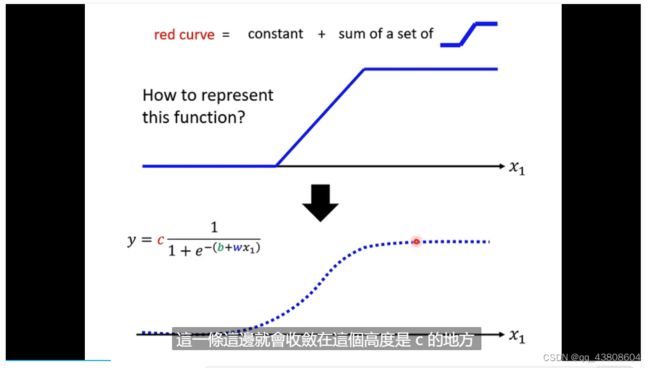
用sigmoid function来表示这样的曲线,sigmoid意为S型,用这个sigmoid去逼近蓝色的曲线,多个sigmoid加起来逼近合适的曲线
多个sigmoid相加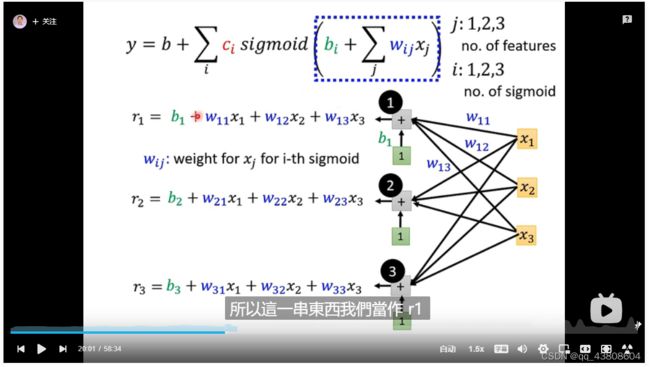

可以把这样的式子计算写为矩阵相乘

未知的参数很多了,就改为L(Osetae)


随机选择一个setae,对L求在setae0时的偏导数,所组成的向量就是梯度向量,右边是根据g来更新到setae1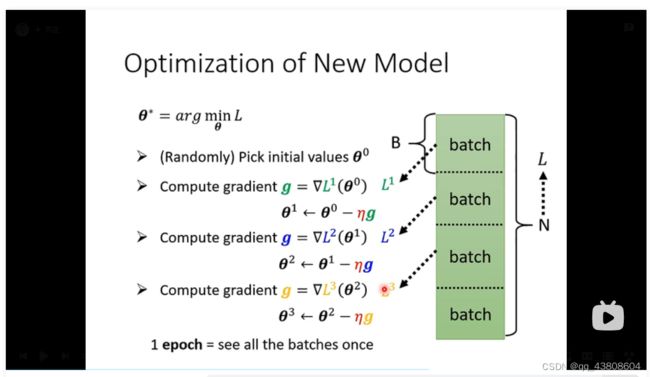
我们并不会拿一个大L算gradient,我们会先算L1(即第一个batch来更新一个setae1),再计算L2(更新第二个setae2),以此类推,更新到最后一个最新的setae参数。每一次更新参数叫做一次update,把所有的batch都看过一次叫做一个epoch
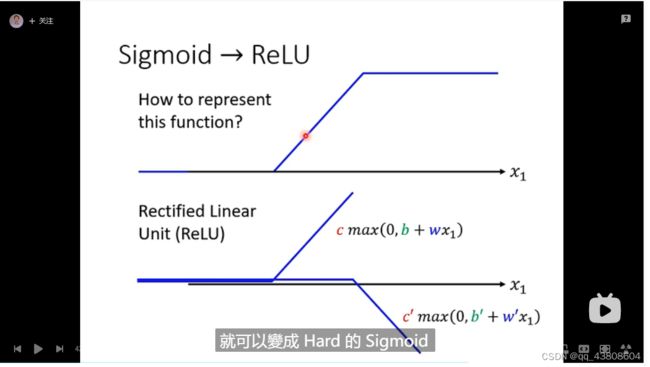
soft sigmoid是中间光滑的一段曲线,而hard sigmoid是中间有尖点的一段折线,ReLU是hard sigmoid的拼接版,ReLU的表达式为cmax(0,b+wx)
class MyModel(nn.Module):
def __init__(self):
super(MyModel, self).__init__()
self.net = nn.Sequential(
nn.Linear(10, 32),
nn.Sigmoid(),
nn.Linear(32, 1)
)
def forward(self, x):
return self.net(x)
class MyModel2(nn.Module):
def __init__(self):
super(MyModel2, self).__init__()
self.layer1 = nn.Linear(10, 32)
self.layer2 = nn.Sigmoid()
self.layer3 = nn.Linear(32, 1)
def forward(self, x):
out = self.layer1(x)
out = self.layer3(out)
out = self.layer3(out)
return out
这两种是一样的效果
● Mean Squared Error (for regression tasks)
criterion = nn.MSELoss()
● Cross Entropy (for classification tasks)
criterion = nn.CrossEntropyLoss()
● loss = criterion(model_output, expected_value)
损失函数的定义效果
神经网络的搭建过程
//随机梯度下降法
dataset = MyDataset(file) #read data via MyDataset
tr_set = DataLoader(dataset, 16, shuffle=True) #put dataset into Dataloader
model = MyModel().to(device) #construct model and move to device (cpu/cuda)
criterion = nn.MSELoss() #set loss function
optimizer = torch.optim.SGD(model.parameters(), 0.1) #set optimizer
//模型训练
for epoch in range(n_epochs): #迭代次数
model.train() #进入模型调试模式
for x, y in tr_set: #迭代导入set的参数
optimizer.zero_grad() #将上一次的梯度归零
x, y = x.to("cpu"), y.to("cpu") #将数据移动到device(cpu/cuda)中
pred = model(x) #计算一次输出参数
loss = criterion(pred, y) #计算损失
loss.backward() #计算梯度
optimizer.step() #最佳化损失函数,注意uodate是更新一次batch,epoch是更新一次大L,大L包含数个batch
//模型Validation
#Neural Network Validation Loop
model.eval() #将模型设置为测试模式
total_loss = 0 #设置一个total_loss
for x, y in dv_set: #迭代输入参数
x, y = x.to("cpu"), y.to("cpu")
with torch.no_grad(): #关闭梯度计算
pred = model(x) #计算输出
loss = criterion(pred, y) #计算损失
total_loss += loss.cpu().item() * len(x) #相加总损失
avg_loss = total_loss / len(dv_set.dataset) #计算平均损失
#Neural Network Testing Loop
model.eval()
preds = []
for x in tt_set: #迭代统计模型输出数据
x = x.to("cpu")
with torch.no_grad():
pred = model(x)
preds.append(pred.cpu()) #将数据转化为cpu tensor或者cuda tensor(用.to("cuda"))来转换
#save/load trained models
torch.save(model.state_dict(), path)
ckpt = torch.load(path)
model.load_state_dict(ckpt)