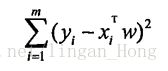第8章 机器学习实战之线性回归

第二部分 回归

写在前面：

回归是监督学习的方法的延续。
监督学习指的是有目标变量或预测目标的机器学习方法 。
回归与分类的不同，就在于其目标变量是连续数值型 。分类输出的是标称型类别值。

---

主要内容：
● 线性回归
● 局部加权线性回归
● 岭回归和逐步线性回归
● 预测鲍鱼年龄和玩具售价

分类的目标变量是标称型数据，下面我们会对连续型的数据做出预测。

8.1 用线性回归找到最佳拟合曲线
优点：结果易于理解，计算上不复杂
缺点：对非线性的数据拟合不好
适用数据类型：数值和标称型数据

回归的目的是预测数值型的目标值。
最直接的方法就是依据输入写出一个目标值得计算公式。
假如想要预测姐姐的男友汽车功率的大小，可能需要下面这个公式：

HorsePower = 0.0015 * annualSalary - 0.99 * hoursListenimgToPulicRadio

这就是所谓的回归方程(regression equation) ，其中 0.0015 - 0.99 称作 回归系数(regression weights) ，求回归系数的过程就是回归。
具体的做法就是用回归系数乘以输入值，再将结果全部加在一起，就得到了预测值（这些运算就是求出二者的内积）。

值得一提的是，存在一种非线性回归的回归模型，该模型认为输出可能是输入的乘积，上面的功率计算公式也可以这样写：

HorsePower = 0.0015 * annualSalary / hoursListenimgToPulicRadio

回归的一般方法
（1）收集数据：采用任意方法收集数据
（2）准备数据：回归需要数值型数据，标称型数据将被转换成二值型数据。
（3）分析数据：绘制出数据的可视化二维图将有助于对数据做出理解和分析，在采用缩减法求得新的回归系数之后，可以将新拟合绘在图上作为比对。
（4）训练算法：找到回归系数
（5）测试算法：使用R2或者预测值和数据的拟合度，来分析模型的效果
（6）使用算法：使用回归，可以在给定输入的时候预测一个数值，这是对分类方法的提升，因为这样可以预测连续型数据而不仅仅是离散的类别标签。

假定输入的数据存放在矩阵 X 中 ，回归系数存放在向量 w 中。那么对于给定的数据X1，预测结果将会通过Y1 = X1^T * w 。
如果我们知道X对应的Y，如何找到w呢？方法就是找到使用误差最小的w 。这里的误差指的是预测y值和真是y值之间的差值。使用该误差的简单累加将使得正差值和负差值相互抵消，所以采用平方误差。

平方误差可以写为：

用矩阵表示还可以写作： (y - Xw)^T (y - Xw)-
若对w进行求导： 得，X ^(Y - Xw)
令 X ^(Y - Xw) = 0
解得（当前估计出的w的最优解）

上述的(X^T * X)^-1 ，这个公式是对矩阵求逆，但是矩阵的逆可能不存在，所以代码里面需要加一个判断条件。求解最佳w的方法也称之为 OLS，普通最小二乘法。

# 标准回归函数和数据导入函数 

def loadDataSet(fileName):
    """
    函数能够自检出特征的数目
    """
    numFeat = len(open(fileName).readline().split('\t')) - 1
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat, labelMat

#求最佳拟合直线
def standRegres(xArr,yArr):
    xMat = np.mat(xArr); yMat = np.mat(yArr)
    xTx = xMat.T * xMat 
    #判断矩阵是否可逆,np.linalg.det()矩阵求行列式（标量）
    if np.linalg.det(xTx) == 0.0:   
        print "This matrix is singular, cannot do inverse"
        return
    #ws = xTx.I * (xMat.T * yMat)
    ws = np.linalg.solve(xTx, xMat.T * yMat.T)
    return ws 

np.linalg.inv()：矩阵求逆
np.linalg.det()：矩阵求行列式（标量）

调用矩阵求行列式，如果行列式结果不为零，说明矩阵的逆是存在的。
其实对于上述代码，如果我们调用numpy下面的linalg线性代数库，我们的代码还可以写为：

ws = np.linalg.solve(xTx, xMat.T * yMatT)

In [3]: import regression

In [4]: reload(regression)
Out[4]: <module 'regression' from 'regression.pyc'>

In [5]: xArr,yArr = regression.loadDataSet(r"E:\ML\ML_source_code\mlia\Ch08\ex0.txt")

In [6]: ws = regression.standRegres(xArr,yArr)

In [7]: ws
Out[16]:
matrix([[ 3.00774324],[ 1.69532264]])

得到的结果ws，里面就存放着回归系数。
我们知道 xArr[:2] = [[1.0, 0.067732], [1.0, 0.42781]]
X0 = 1.0
我们假定偏移量就是一个常数。
在用内积预测y的时候，第一维将乘以前面的常数X0 ， 第二维将乘以变量X1 。
假定X0 = 1，得 y = ws[0] + ws [1] *X1
这个y是实际预测给出的。

In [39]: xMat = np.mat(xArr)
    ...:
In [40]: yMat = np.mat(yArr)
    ...:
In [41]: yHat = xMat * ws   #预测值
    ...:

In [42]: fig = plt.figure()
    ...:
0xbcab8d0>

In [43]: ax = fig.add_subplot(111)
    ...:
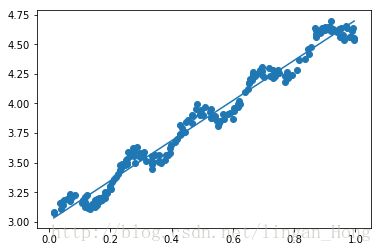
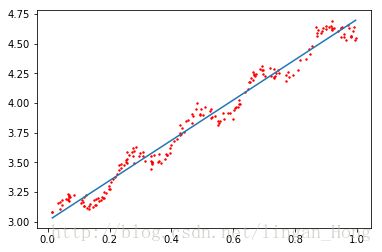
In [44]: ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0])
    ...:
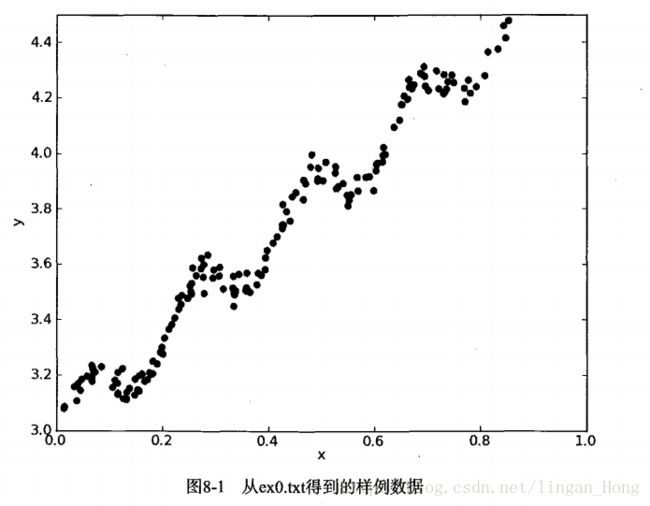
Out[44]: 0xbfb5e48>

绘制数据集散点图好热最佳拟合曲线。
为了防止所绘制曲线出现问题，我们要将点按照升序排列：

In [45]: xCopy = xMat.copy()
    ...:
In [46]: xCopy.sort(0)
    ...:
In [47]: yHat = xCopy * ws
    ...:

In [48]: ax.plot(xCopy[:, 1], yHat)
    ...:
Out[48]: [0xcfdc3c8>]

In [49]: plt.show()

几乎任一数据集都可以用上述的方法建模。那么该如何判断模型的好坏呢？
其实我们可以计算预测值yHat序列 和真实值 y 序列的的匹配程度，也就是这两个序列的相关系数。

numpy的corrcoef (yEstimate , yActual) 来计算预测值和真实值的相关性。
例子：
计算y的预测值yHat

In [14]: yHat = xMat * ws

计算相关系数

In [15]: np.corrcoef(yHat.T, yMat )
Out[15]:
array([[ 1. , 0.98647356],
       [ 0.98647356, 1. ]])

得到的结果显示对角线上的数据是1.0，yMat和自己匹配是最完美的。
yHat和yMat的相关系数是0.98

8.2 局部加权线性回归

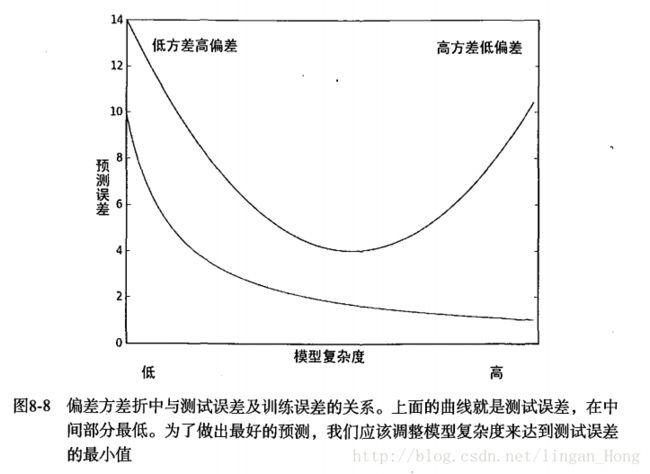
因为线性回归求得具有最小均方误差的无偏估计。所以他可能出现欠拟合现象。
模型欠拟合将不能有好的预测结果，所以有些方法允许在估计中引入一些偏差，从而降低预测的均方误差。
其中一个方法是局部加权线性回归（LWLR），我们给待预测点附近的每个点赋予一定的权重，然后在这个子集上基于最小均值方差来进行普通的回归。每次预测均需要事先选取出对应的数据子集。
这个算法解出的回归系数如下：

    w = (X^T WX)^-1 * X^TWy

其中w是一个矩阵，用来给每一个点赋予权重。
LWLR使用的类似于支持向量机中的“核函数”来对附近的点赋予更高的权重。
核的类型可自由选择，最常用的就是高斯核。高斯核公式如下：

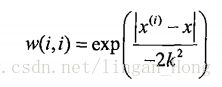
如此，就构建了一个只含有对角元素的权重矩阵，且点x与x(i)越近，则w(i , i)将会越大。
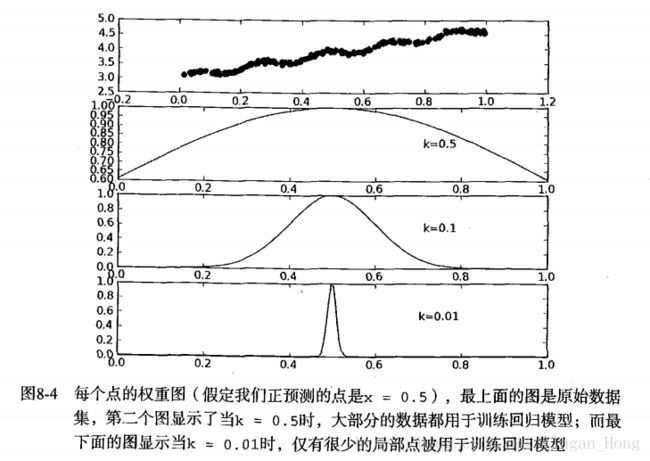
指定参数k决定了对附近的点赋予多大的权重。

# 局部加权线性回归函数
def lwlr(testPoint, xArr, yArr, k = 1.0):
    xMat = np.mat(xArr); yMat = np.mat(yArr).T
    m = np.shape(xMat)[0]
    weights = np.mat(np.eye((m)))  #创建对角权重矩阵
    for j in range(m):
        diffMat = testPoint - xMat[j, :]
        #权重大小以指数级衰减
        weights[j, j] = np.exp(diffMat * diffMat.T/(-2.0*k**2))  
    xTx = xMat.T * (weights * xMat)
    if np.linalg.det(xTx) == 0.0:   #矩阵行列式 
        print "This matrix is singular, cannot do inverse"
        return
    #ws = xTx.I * (xMat.T * (weights * yMat))
    ws = np.linalg.solve(xTx, xMat.T * (weights * yMat))
    return testPoint * ws 


def lwlrTest(testArr, xArr, yArr, k = 1.0):
    m = np.shape(testArr)[0]
    yHat = np.zeros(m)
    for i in range(m):
        yHat[i] = lwlr(testArr[i], xArr, yArr, k)
    return yHat

测试结果：

In [16]: reload(regression)
Out[16]: 'regression' from 'regression.py'>

In [17]: xArr,yArr = regression.loadDataSet(r"E:\ML\ML_source_code\mlia\Ch08\ex0.txt")

In [18]: yArr[0]
Out[18]: 3.176513

In [23]: regression.lwlr(xArr[0], xArr, yArr, 1.0)
Out[23]: matrix([[ 3.12204471]])

In [24]: regression.lwlr(xArr[0], xArr, yArr, 0.001)
Out[24]: matrix([[ 3.20175729]])

In [25]: regression.lwlr(xArr[0], xArr, yArr, 0.003)
Out[25]: matrix([[ 3.20200665]])

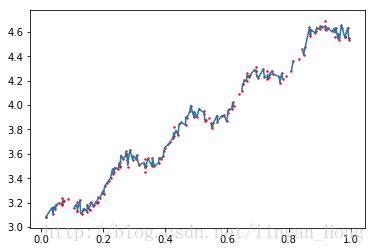
In [36]: yHat = regression.lwlrTest(xArr, xArr, yArr, 0.003)
            xMat = np.mat(xArr)
    ...:

In [38]: srtInd = xMat[:,1].argsort(0)
    ...:

In [39]: xSort = xMat[srtInd][:, 0 ,:]
    ...:

In [41]: fig = plt.figure()
    ...:
0xba37208>

In [45]: ax = fig.add_subplot(111)
    ...:

In [46]: ax.plot(xSort[:,1],yHat[srtInd])
    ...:
Out[46]: [0xbcca7f0>]

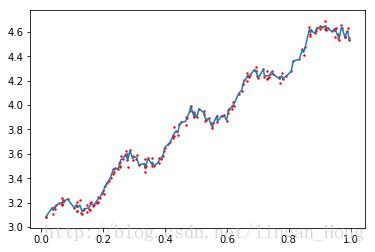
In [47]: ax.scatter(xMat[:,1].flatten().A[0], np.mat(yArr).T.flatten().A[0],s=2,c='red')
    ...: plt.show()

k=0.03，考虑了太多的噪音，导致过拟合。

k=0.01 ，模型可以挖掘出数据潜在的规律。

k= 1.0 ，模型的效果与最小二乘法差不多

8.3 预测鲍鱼的年龄
鲍鱼的年龄可以从鲍鱼壳的层数推断。

In [6]: def rssError(yArr, yHatArr):
   ...: return ((yArr - yHatArr)**2).sum()
   ...:
   ...:
In [7]: abX,abY = regression.loadDataSet(r'E:\ML\ML_source_code\mlia\Ch08\abalone.txt')

In [9]: yHat01 = regression.lwlrTest(abX[0:99], abX[0:99], abY[0:99], 0.1)
   ...: yHat1 = regression.lwlrTest(abX[0:99], abX[0:99], abY[0:99], 1.0)
   ...: yHat10 = regression.lwlrTest(abX[0:99], abX[0:99], abY[0:99], 10)
   ...:

为了分析预测误差的大小，使用函数rssError()来计算这个指标

In [10]: regression.rssError(abY[0:99], yHat01.T)
    ...:
Out[10]: 56.782844739243856

In [11]: regression.rssError(abY[0:99], yHat1.T)
    ...:
Out[11]: 429.89056187017724

In [12]: regression.rssError(abY[0:99], yHat10.T)
    ...:
Out[12]: 549.11817088266241

可以看到，较小的核得到了较小的误差。
如果我们对所有的数据集都使用最小的核，将造成过拟合，对数据的预测效果不一定达到最好。

In [12]: yHat01 = regression.lwlrTest(abX[100:199], abX[0:99], abY[0:99], 0.1)
    ...:
In [13]: regression.rssError(abY[100:199], yHat01.T)
    ...:
Out[13]: 14201.900334127147

In [14]: yHat1 = regression.lwlrTest(abX[100:199], abX[0:99], abY[0:99], 1.0)
    ...:
In [15]: regression.rssError(abY[100:199], yHat1.T)
    ...:
Out[15]: 573.52614418971586

In [16]: yHat10 = regression.lwlrTest(abX[100:199], abX[0:99], abY[0:99], 10)
    ...:
In [17]: regression.rssError(abY[100:199], yHat10.T)
    ...:
Out[17]: 517.57119053826102

核大小等于10的测试误差最小，但是训练集上的误差最大。
我们和简单的线性回归做个比较：

In [16]: ws = regression.standRegres(abX[0:99], abY[0:99])
    ...:
In [20]: yHat = np.mat(abX[100:199]) * ws
    ...:
In [22]: regression.rssError(abY[100:199], yHat.T.A)
    ...:
Out[22]: 518.63631532464842

使用局部加权线性回归来构建模型，可以得到比普通线性回归更好的效果。局部加权线性回归为了做出预测，每次必须保存所有的训练数据。

8.4 缩减系数来“理解”数据
如果数据的特征 比样本点还多，我们不能使用线性回归来做预测。因为计算 (X^TX)^-1 会出错。
特征比样本点多 (n > m) ，输入数据的矩阵 X 是非满秩矩阵。非满秩矩阵求逆会出问题。
（n阶方阵矩阵可逆，则|A|≠0，即|A|是A的n阶非零子式，所以A的秩是n，即A是满秩阵。它是判断矩阵是否可逆的充分必要条件）

为了解决这个问题，我们引入了岭回归。

8.4.1 岭回归
简单来说，岭回归就是在矩阵 X^TX 上加上一个 λJ ，从而使得矩阵非奇异 ，对于(X^TX + λJ ) 可求逆。
其中 矩阵 J 是一个m x m 单位矩阵，对角线上元素全为1，其他元素全部为0 。 λ 是用户自定义的数值。
回归系数计算公式：

w = (X^TX + λJ)^-1 X^T y

岭回归用于特征数大于样本数，也用于在估计中加入偏差。
这里引入 λ 来限制了所有 w 之和，通过引入该惩罚项，能减少不重要的参数，这个在统计学里叫做缩减。缩减法可以去掉其他不重要的参数。因此缩减法能取得更好的预测效果。

岭回归中的岭是什么？
岭回归使用了单位矩阵乘以常数λ ，单位矩阵J，对角线全部是1，其余值全部是0，。在0构成的数据里面出现一条组成的“岭”。这是岭的由来。

这里通过预测误差最小化得到λ ：获取数据之后，首先抽取一部分数据用于测试，剩余作为训练集用于训练参数w，训练完毕后再测试集上测试预测性能。选取不同的λ来重复上述的过程，最终选取一个使预测误差最小的λ 。

#岭回归
def ridgeRegres(xMat, yMat, lam = 0.2):
    xTx = xMat.T * xMat
    denom = xTx + np.eye(np.shape(xMat)[1])*lam
    if np.linalg.det(xTx) == 0.0:   
        print "This matrix is singular, cannot do inverse"
        return
    ws = denom.I * (xMat.T * yMat)                           
    return ws

def ridgeTest(xArr, yArr):
    xMat = np.mat(xArr); yMat = np.mat(yArr).T
    yMean = np.mean(yMat, 0)                 
    yMat = yMat - yMean
    xMeans = np.mean(xMat, 0)
    xVar = np.var(xMat, 0)
    xMat = (xMat - xMeans)/xVar
    numTestPts = 30
    wMat = np.zeros((numTestPts, np.shape(xMat)[1]))
    for i in range(numTestPts):
        ws = ridgeRegres(xMat, yMat, np.exp(i-10))
        wMat[i, :] = ws.T
    return wMat

ridgeRegres() 用于计算回归系数，函数ridgeTest() 用于在一组的 λ 上测试结果。
若lam = 0，结果仍会错误。所以必须限制行列式不为0且lam不等于0。

为了使用岭回归和缩减技术，我们要对特征做标准化处理。使每维特征具有相同的重要性，做法就是 所有特征减去各自的均值并除以方差。

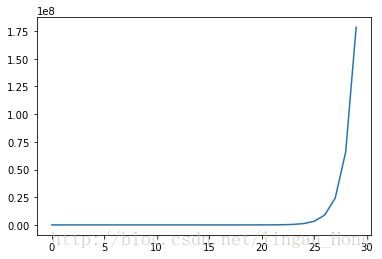
其中，exp(i-10) 以指数函数变化。

In [4]: a=[]

In [5]: for i in range(30):
   ...: a.append(exp(i-10))
   ...:

In [6]: fig = plt.figure()
   ...: ax = fig.add_subplot(111)
   ...: ax.plot(a)
   ...: plt.show()

In [18]: reload(regression)
Out[18]: 'regression' from 'regression.py'>

In [19]: abX,abY = regression.loadDataSet(r'E:\ML\ML_source_code\mlia\Ch08\abalone.txt')

In [22]: ridgeWeights = regression.ridgeTest(abX,abY)

In [37]: import matplotlib.pyplot as plt
    ...:
In [47]: fig = plt.figure()
    ...: ax = fig.add_subplot(111)
    ...: ax.plot(ridgeWeights)
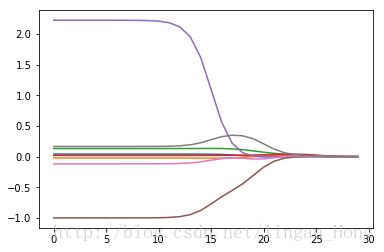
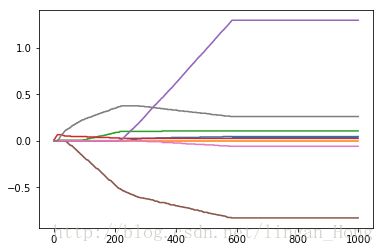
    ...: plt.show()

岭回归的系数变化图。
在图的左边，λ 非常小的时候，系数与普通的回归一样；
在图的右边，系数全部缩减为0；
在中间某个部分可以取得最好的预测结果。

为了定量找到最佳参数，需要交叉验证。

8.4.2 laso
在增加如下约束的时候，普通的最小二乘法回归会得到与岭回归一样的公式 ：

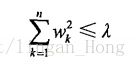
公式表明了回归系数的平方要小于等于λ 。

另一个缩减方法lasso对回归系数租出了限定，约束条件如下：

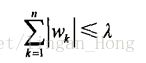
两个公式不不同点在于约束条件使用了绝对值代替了平方。
公式细微的变化极大的增加了计算复杂度。

8.4.3 向前逐步回归
向前逐步回归是一种贪心算法，即每一步都尽可能的减少误差。
开始，所有的权重都设置为1，然后每一步所做的决策是对某个权重增加或减少一个很小的值。

伪代码：

数据标准化，使其分布满足0均值和单位方差
在每轮迭代过程中：
        设置当前最小误差lowestError为正无穷大
        对每个特征：
                增大或缩小：
                        改变一个系数得到一个新的W
                        计算新W下的误差
                        如果误差Error小于当前最小误差lowestError：
                                设置Wbest为当前W
                         将W设置为新的Wbest

In [11]: xArr, yArr = regression.loadDataSet(r'E:\ML\ML_source_code\mlia\Ch08\abalone.txt')

In [11]: regression.stageWise(xArr, yArr, 0.01, 200)
[[ 0. 0. 0. 0. 0. 0. 0. 0.]]
[[ 0. 0. 0. 0.01 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.02 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.03 0. 0. 0. 0. ]]
......
[[ 0.04 0. 0.09 0.03 0.31 -0.64 0. 0.36]]
[[ 0.05 0. 0.09 0.03 0.31 -0.64 0. 0.36]]
[[ 0.04 0. 0.09 0.03 0.31 -0.64 0. 0.36]]
Out[11]:
array([[ 0. , 0. , 0. , ..., 0. , 0. , 0. ],
[ 0. , 0. , 0. , ..., 0. , 0. , 0. ],
[ 0. , 0. , 0. , ..., 0. , 0. , 0. ],
...,
[ 0.05, 0. , 0.09, ..., -0.64, 0. , 0.36],
[ 0.04, 0. , 0.09, ..., -0.64, 0. , 0.36],
[ 0.05, 0. , 0.09, ..., -0.64, 0. , 0.36]])

In [12]: regression.stageWise(xArr, yArr, 0.001, 5000)
[[ 0. 0. 0. 0. 0. 0. 0. 0.]]
[[ 0. 0. 0. 0.01 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.02 0. 0. 0. 0. ]]
[[ 0. 0. 0. 0.03 0. 0. 0. 0. ]]
......
[[ 0.043 -0.011 0.12 0.022 2.023 -0.963 -0.105 0.187]]
[[ 0.044 -0.011 0.12 0.022 2.023 -0.963 -0.105 0.187]]
[[ 0.043 -0.011 0.12 0.022 2.023 -0.963 -0.105 0.187]]
[[ 0.044 -0.011 0.12 0.022 2.023 -0.963 -0.105 0.187]]
Out[10]:
array([[ 0. , 0. , 0. , ..., 0. , 0. , 0. ],
[ 0. , 0. , 0. , ..., 0. , 0. , 0. ],
[ 0. , 0. , 0. , ..., 0. , 0. , 0. ],
...,
[ 0.043, -0.011, 0.12 , ..., -0.963, -0.105, 0.187],
[ 0.044, -0.011, 0.12 , ..., -0.963, -0.105, 0.187],
[ 0.043, -0.011, 0.12 , ..., -0.963, -0.105, 0.187]])

把结果与最小二乘法进行比较，得到结果如下：

In [13]: xMat = np.mat(xArr)

In [14]: yMat = np.mat(yArr).T

In [15]: xMat =regression.regularize(xMat)

In [16]: yM = np.mean(yMat,0)

In [17]: yMat = yMat - yM

In [19]: weights = regression.standRegres(xMat,yMat.T)

In [20]: weights.T
Out[20]:
matrix([[ 0.0430442 , -0.02274163, 0.13214087, 0.02075182, 2.22403814,
-0.99895312, -0.11725427, 0.16622915]])

In [22]: aaa= regression.stageWise(xArr, yArr, 0.005, 1000)
In [23]: fig = plt.figure()
    ...: ...: ax = fig.add_subplot(111)
    ...: ...: ax.plot(aaa)
    ...: ...: plt.show()

8.5 权衡偏差与方差