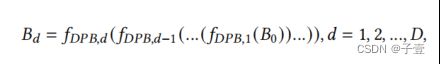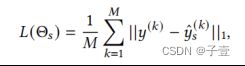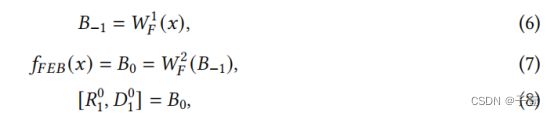《Efficient Single Image Super-Resolution Using Dual Path Connections with Multiple Scale Learning》

目录

一、引言：

二、网络部分：

1、整体

2、FEB：

3、DPB：

4、DPU:

5、过渡单元TU：

6、HFIB(Hierarchical Feature Integration Block )： 

7、RB：

实验：

细节：

消融实验：

多尺度学习的效果：

双路径连接（DPC）的效果:

和SOTA方法的比较：

模型的复杂度和推理时间：

---

一、引言：

本文作者提出了使用双重路径连接和多尺度学习的高效网络，称为EMSRDPN。

原因有二：其一，残差连接和稠密连接已经被广泛用于简化前馈信息和反向梯度传播，以提高性能。不过，当前的方法在大多数网络层中是以次优的方式分别使用残差连接和稠密连接。其二，虽然设计各种网络和方法来提高计算效率，节约参数，或利用多尺度因子的训练数据来提高性能，然而这样除了会在HR空间引起高计算成本，还不能在不同尺度的模型中共享参数以节省参数和推理时间。

作者将双路径连接引入到EMSRDPN中，它在大多数网络层中以集成的方式使用残差连接和稠密连接。双路径连接有两个优点：既可以重用残差连接的共同特征，又可以探索稠密连接的新特征，以学习SISR的好的表示。

EMSRDPN，通过在一个非常深的卷积神经网络中引入双路径连接和多尺度训练和推理。利用双路径连接，EMSRDPN在大多数卷积层中以集成的方式使用残差和稠密连接，再借用残差连接来重用共同特征，利用稠密连接来探索新特征，以学习SISR的良好表示。

EMSRDPN又通过在不同尺度因子之间共享大部分参数，相互使用不同尺度因子的训练数据，在训练过程中利用特征相关性，在推理过程中摊销不同尺度因子之间的大部分参数和计算，又可以提高网络的参数效率和推理时间。

二、网络部分：

1、整体

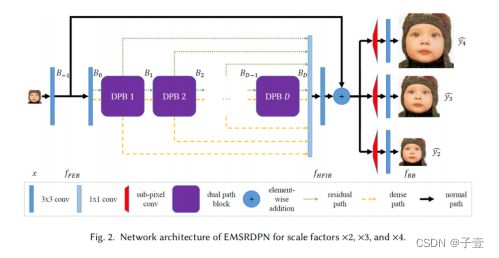
EMSRDPN包括四个部分如图2所示，第一部分是特征提取块（FEB），从下采样LR图像提取低级特征，第二部分是多个堆叠双路径块（DPBs），从低级特征学习丰富的层次特征，每个DPB是由几个级联双路径单元（DPUs）和一个过渡单元组成，第三部分是分层特征集成块（HFIB），它融合了所有DPB和FEB输出的丰富的层次特征图，使信息直接向前传播，缓解梯度消失/爆炸问题，最后一部分分别是针对不同尺度因子的多个并行重建块（RBs）。

FEB、DPBs和HFIB在不同的尺度因子之间共享。EMSRDPN是一种针对多尺度因子的多任务超分辨率学习和推理网络，可以利用不同尺度因子的超分辨率任务的训练数据，利用特征相关性相互帮助，提高性能，同时节省参数数量和模型的推理时间。网络的关键组成部分是双路径单元，它将残差和稠密连接无缝地集成在一层中。为了建立一个深度网络，作者在每个双路径块中添加一个过渡单元来融合残差和稠密特征，以控制计算成本和内存消耗。

首先，在FEB中使用两个卷积层，从网络输入x中提取低层次的特征(x表示将被放大的降采样LR图像)，

 其次，使用多个堆叠的DPB从低级特征中学习丰富的层次特征。

再使用HFIB集成了所有DPBs和FEB输出的丰富的层次特征图

最后，使用HFIB输出的集成特征作为特定于尺度因子s的RB的输入，来重建HR图像y

损失函数：         

是针对倍数s的参数，其中包括FEB、DPBs、HFIB中的共享参数，以及RB中对应于尺度因子的独有参数。请注意，在使用标准训练数据集进行训练时，作者只有一个HR图像和不同比例因子下不同的LR图像，但在测试过程中，可以从一个LR图像中推断出多个SR图像。

2、FEB：

FEB使用两个3×3卷积层从LR图像中提取低层次的特征。为了与dpb保持一致，作者还将它的输出视为两部分，残差和密集部分，

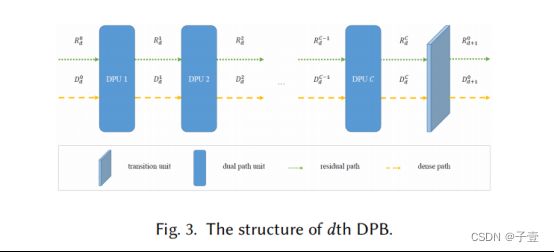
3、DPB：

每一个DPB由若干个级联的DPU和一个过渡单元TU组成，假定有D个DPB，每个DPB有C个DPU

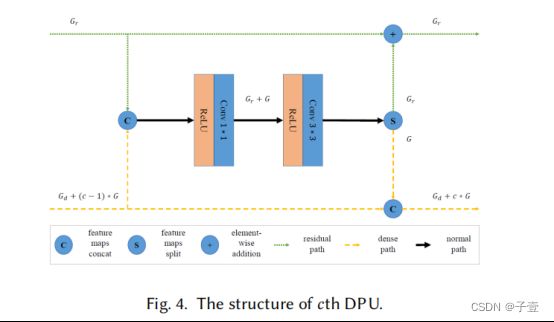
4、DPU:

 

 每个DPU首先连接残差部分和密集部分的输入特征映射，然后非线性转换连接输入特征映射，因为作者采用“预激活”设计残差网络[17]，最后使用瓶颈设计包括1×1卷积层其次是3×3卷积层学习残差函数和新的密集特性，同时保持计算和内存预算低，

接下来，它将输出分成两部分，残差函数添加到输入的残差部分，新的密集特征连接到输入的密集部分

 

最后，将残差函数加（add）到输入特征映射的残差部分上，形成“残差路径”。

 

将新学习到的密集特征连接（concat）到输入特征映射的密集部分，形成“密集路径”，

相比较于SRDPN,根据[34]EDSR去除批处理归一化层，并将非线性变换更改为ReLU，以提高计算量和内存效率。

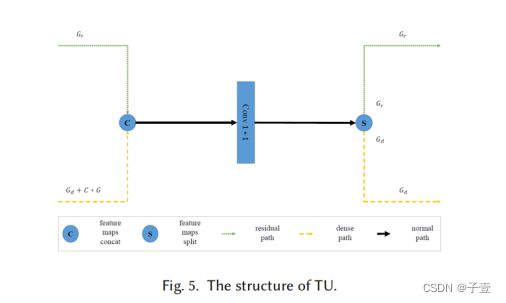
5、过渡单元TU：

因为每个DPB中每个DPU的密集路径会把它输出的密集部分concat到它的输入特征图的密集部分，也就是将之前DPU输出的所有密集部分和当前DPB中第一个DPU输入的密集部分concat到一起，就是密集连接的感觉，当前输入是之前所有层的输出。

假设输入特征图到第一个DPU具有Gr个残差路径特征和Gd个密集路径特征，每个DPU的密集路径增长速率为G，在dth DPB，之后，会得到Gr残差路径特征和（Gd+C*G）密集路径特征作为第（d+ 1）个DPB.的输入.

 每个过渡单元还将其输入特征图作为两个部分，即残差部分和密集部分，由当前DPB中的最后一个DPU输出。

TU在 DPB中的函数表述如下：

 

6、HFIB(Hierarchical Feature Integration Block )： 

 在HFIB块中，作者首先将所有DPB的输出concat起来，以便使用多个堆叠DPB学习到的丰富的层次特征，

然后使用1×1的卷积层将特征空间转换为低维空间，以降低计算成本和内存消耗，最后使用3×3卷积层学习全局残差函数添加到FEB的第一个卷积层的输出中，改进正向信息和反向梯度流，

7、RB：

为了使用训练数据的多个尺度因素相互利用特征相关性提高性能和提高参数效率和推理时间的模型，作者分别对不同尺度因子使用多个并行RBs，对EMSRDPN中的不同尺度因子共享FEB、DPBs和HFIB，可以一次生成不同尺度因子的HR图像。根据训练数据的可用性和应用的需求，可以灵活配置RBs的数量和相应的尺度因子。在特定尺度因子s的重构块（RB）中，作者使用不同尺度因子共享的层次特征集成块（HFIB）的输出作为一个有效的亚像素卷积层的输入，然后使用3 × 3卷积层对HR图像进行比例因子s的重构：

实验：

细节：

作者构建了一个具有（D=16）dpb的网络，每个DPB都有（C=4）dpu。网络残差路径的宽度设置为 64，网络基本密集路径的宽度设置为 64，即TU和FEB密集部分的宽度，网络密集路径的增长率设置为 64，即DPU密集部分的宽度。FEB和RBs中卷积层的输出特征图的宽度设置为（Gr+Gd），但RBs中最后3个×3个卷积层的输出是与不同尺度因子对应的多个重构HR彩色图像。除了dpu、TUs和HFIB中的过渡层外，所有层都使用3×3卷积内核，这些过渡层使用1×1卷积内核来融合特性，降低计算和内存成本。

消融实验：

多尺度学习的效果：

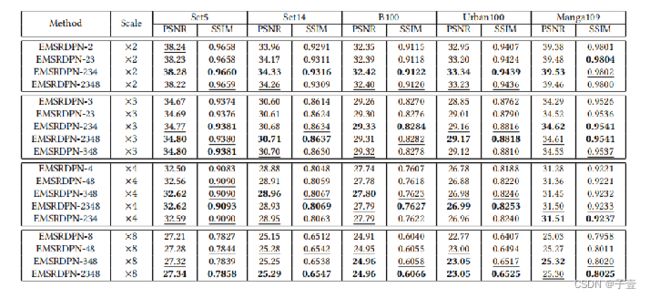
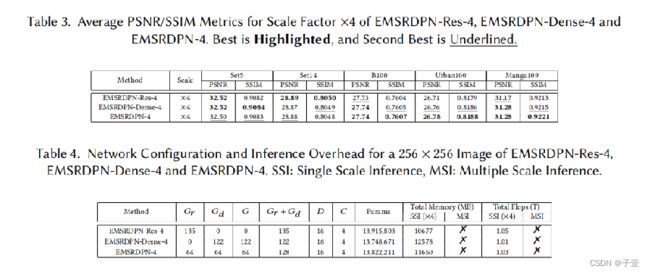
作者设计了三组实验来研究尺度对模型效果的影响：第一组，对于各尺度分别训练，即在每个尺度都只用一个重构块，分别标记为 EMSRDPN-2、EMSRDPN-3, EMSRDPN-4, EMSRDPN-8；第二组：从尺度因子×2的单尺度模型开始，根据×3、×4、×8的顺序，依次增加一个尺度因子，即按顺序训练含有2、3、4个尺度因子的模型，分别记为EMSRDPN-2, EMSRDPN-23,EMSRDPN-234, EMSRDPN-2348；第三组：再从尺度因子×8的单尺度模型开始，根据×4、×3、×2的顺序，每次增加一个尺度因子，训练含有2、3、4个尺度因子的模型，分别记为EMSRDPN-8, EMSRDPN-48, EMSRDPN-348,EMSRDPN-2348。不同组中的相同模型只被训练了一次。

注意：每个尺度都只去对应的尺度倍数， · ×3、×4、×8均受益于多尺度训练的意思是，比如3倍。那一定是3倍里边，其他的倍数不需要看，相对于单尺度的值，多尺度的值一定是增加的，其他的以此类推。

 

两个发现：

1： ×3、×4、×8均受益于多尺度训练，性能随着训练尺度因子数量的增加而提升 ·

2：x2受益于多尺度训练，最多有三个训练尺度因子，包括EMSRDPN-23、EMSRDPN-234模型，但对于四个训练尺度因素的模型，即EMSRDPN-2348，性能指标略有下降。作者认为，这是因为×8的大尺度因子的LR图像与×2的小尺度因子的LR图像模式有很大的不同，从而恶化了这两个尺度因子的特征相关性。 根据这些观察和分析，选择EMSRDPN-2348作为最终模型，缩写为EMSRDPN，以与最先进的SISR方法进行比较，以在重建性能、参数和推理效率之间实现良好的权衡。 

此外，作者还研究了EMSRDPN模型的多尺度推理对效率的影响。EMSRDPN模型的多尺度推理能力可以在多个尺度因子之间摊销参数、内存消耗和计算量。与EMSRDPN-8这样的单尺度模型相比，EMSRDPN模型只添加了边缘参数，并且与使用EMSRDPN-8对×8这样的单尺度因子进行推断相比，只添加了边缘内存消耗和边缘计算。EMSRDPN模型的多尺度推理开销仅为使用单尺度模型的四分之一。

双路径连接（DPC）的效果:

由于残差连接和密集连接是所提出的双路径连接的特殊情况，作者将Gd和G设置为0来构成只有残差网络结构的模型，或者将Gr设置为0构成只有密集网络结构的模型。这样，可以通过限制三种结构的参数，研究双路径结构与纯残差网络结构和密集网络结构对性能的影响。 作者利用不同结构的模型只训练了×4的网络。

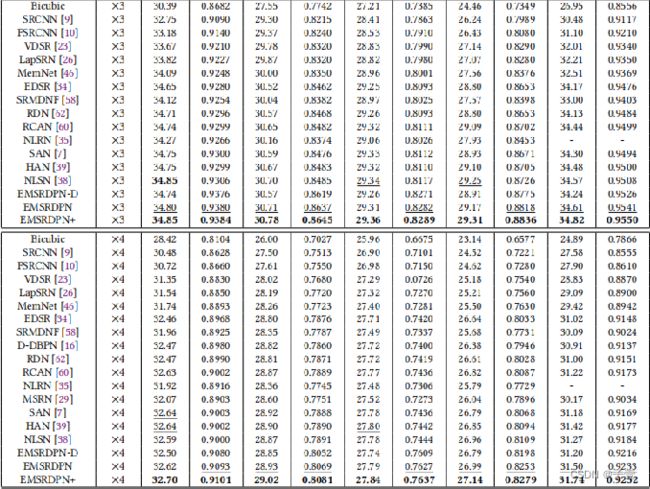
和SOTA方法的比较：

视觉比较显示，该方法重建了更多的高频细节，如图像的边缘和纹理，并具有更少的伪影。

 

 

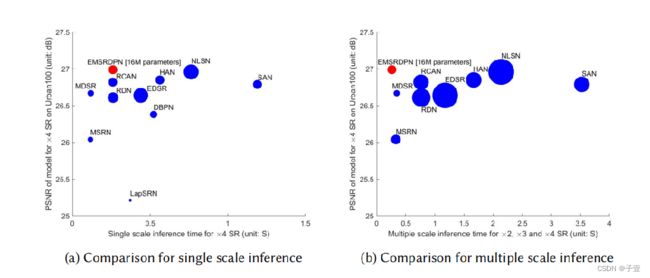
模型的复杂度和推理时间：