【论文阅读】使用周期一致的对抗网络的非匹配的图片到图片的翻译
Unpaired Image-Image Translation using Cycle-Consistent Adversarial Networks
论文地址:https://arxiv.org/abs/1703.10593
发表日期:15/11/2018
项目地址:https://github.com/junyanz/CycleGAN。
高能预警:这篇文章将告诉你如何将苹果变成橘子,马变成斑马。
图 1:给定两个无序图片集,我们的算法学习如何自动地把一幅图片转换为其他版本,并且反之亦然:例如将普通照片转换为莫奈风格的图像。
简介:
对于一些任务,将训练数据成对数据进行对齐是不可行的。我们提供了一种方法:我们的任务是学习一个映射G:X→Y 这样的话来自G(X)的分布和Y是不可辨认的,使用一个对抗损失(adversarial loss)。因为这种映射是及其欠约束的,所以我们使用了逆向的映射F:Y→X 并且引入了周期一致损失来迫使F(G(X))≈X(反之亦然)。我们的网络可以完成一些不可思议的任务,比如物体变形、季节变换、照片增强等。
1 介绍
1873年,一个可爱的春天早晨,美丽的塞纳河倒映着蓝的如同水晶的天空。克劳德·莫奈先生,享誉世界的法国画家,描绘出的了著名的《阿让特伊,塞纳河》。借助莫奈先生的其他作品,通过神经网络,使得我们能够身临其境。
2015年,我在一片无边无际的麦田里,一阵秋风袭来,麦子形成巨浪。我们想知道,莫奈先生在此时会描绘出怎样的画面。借助莫奈先生的其他作品,通过神经网络,使得我们能够观赏到莫奈先生的跨时空名画。
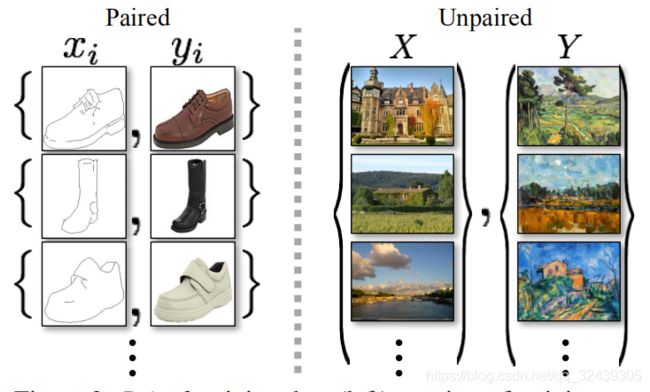
图 2:匹配的训练数据(左),我们取而代之,考虑一些不匹配数据
包括一个源头 { x i } i = 1 N ( x i ∈ X ) { \{x_{i} \}}_{i=1}^{N}(x_{i}\in X) {xi}i=1N(xi∈X)和目标 { y j } j = 1 N ( y j ∈ Y ) { \{y_{j} \}}_{j=1}^{N}(y_{j}\in Y) {yj}j=1N(yj∈Y)。
理论上,这个目标能够指示一个输出分布 y ^ \hat y y^与经验分布 p d a t a ( y ) p_{data}(y) pdata(y)相符合(通常,这需要G足够混乱)。最优的G能够将领域X转换到领域 Y ^ \hat Y Y^分布与Y相似。但是,这种映射并不保证单独的输入x和输出y有意义的匹配,因为有很多映射G。而且,实践上,我们发现优化隔离的对抗的目标很困难:标准的步骤总是导致臭名昭著的问题“模式崩溃”,所有的输入图片映射到同样的输出图片,优化工作陷入僵局。
因此我们想到映射的可逆性,提出了"周期一致性"的损失来解决上述问题。
2 相关工作
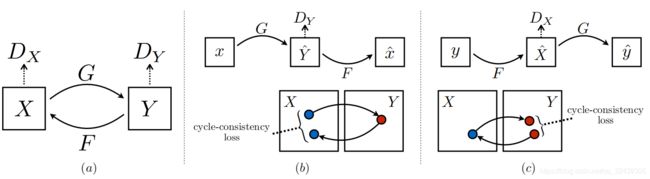
图 3:(a)我们的模型包括两个映射:G: X→Y, F:Y→X, 以及联合的对抗鉴赏器 D Y D_{Y} DY和 D X D_{X} DX。 D Y D_{Y} DY促使G将X翻译为领域Y的输出,反之亦然。为了正则化映射,我们引入了两个周期一致损失。(b)前向的周期一致性损失 x→G(x)→F(G(x))≈x,(c)反向的一致性损失。
3 公式
3.1 对抗损失
对于映射G: X→Y 和它的鉴赏器 D Y D_{Y} DY,公式为:
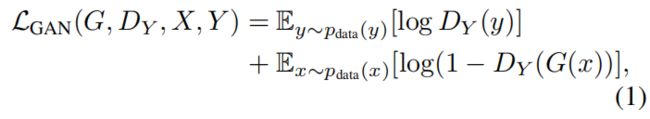
这里G 尝试生成图片G(x),与领域Y图片相似,而 D Y D_{Y} DY目标是辨别图片G(x)和真实样本 y y y。G目标是最小化目标函数,而对手D则尝试最大化之。即 m i n G m a x D y L G A N \underset {G}{min} \quad \underset{D_{y}}{max} L_{GAN} GminDymaxLGAN,对于逆过程,我们采用 L G A N ( F , D x , Y , X ) L_{GAN}(F,D_{x},Y,X) LGAN(F,Dx,Y,X).
3.2 周期一致性损失
为了尽可能减少映射函数的可能情况,我们定义了周期一致性损失:
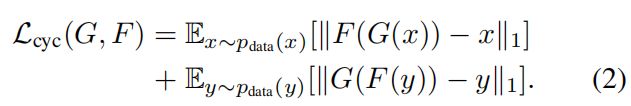
这里的||·||是L1范数的意思。早期的实验中,我们尝试把L1范数替换为对抗损失,但是并没有得到很好的效果的提升。
图 4:输入,输出和重构过程。
3.3 完整目标

这里 λ \lambda λ控制了两个物体的相对重要性。我们目标是解决:

注意,我们的模型可以看作是训练两个“自动编码器”。
4 实现
训练细节 我们运用了两种方法来稳定训练过程。首先,对于 L G A N L_{GAN} LGAN我们将负的log目标替换为最小平方损失(a least-squares loss)。尤其是,对于GAN损失 L G A N ( G , D , X , Y ) L_{GAN}(G,D,X,Y) LGAN(G,D,X,Y),我们训练G以最小化 E x ∼ p d a t a ( x ) [ ( D ( G ( x ) ) − 1 ) 2 ] \mathbb E_{x\sim p_{data}(x)}[(D(G(x))-1)^2] Ex∼pdata(x)[(D(G(x))−1)2],并且训练D来最小化 E y ∼ p d a t a ( y ) [ ( D ( y ) − 1 ) 2 ] + E x ∼ p d a t a ( x ) [ ( D ( G ( x ) ) ) 2 ] \mathbb E_{y\sim p_{data}(y)}[(D(y)-1)^2]+\mathbb E_{x\sim p_{data}(x)}[(D(G(x)))^2] Ey∼pdata(y)[(D(y)−1)2]+Ex∼pdata(x)[(D(G(x)))2]。其次,为了减少模型振荡,我们更新鉴赏器,使用生成了一段时间的图像而不是最近的生成器输出。我们建立一个图像缓存区,缓存了50张之前的图片。
对于所有的实验,我们设置 λ = 10 \lambda=10 λ=10(公式3)。使用Adam优化器,batchsize = 1.所有的网络从头开始训练,学习率为2e-4。我们在前100个epoch保持学习率不变,并在接下来的100个周期将学习率线性减为0。
5 结果
5.1评估
5.1.1 评价策略
AMT感知研究在地图上的照片任务中,我们对Amazon Mechanical Turk(AMT)进行了“真实与虚假”的感知研究,以评估我们出局的真实性。我们遵循Isola等人的相同感知研究方案。 除了我们只测试了每个算法的25个参与者的数据。参与者被展示了一系列图像,一个是真实的照片或地图,一个是假的(由我们的算法或基线生成),并要求点击他们认为是真实的图像。每个阶段的前10个试验都是实践,并且反馈是否参与者的反应是正确的还是不正确的。剩下的40个试验用于评估每个算法欺骗参与者的速率。每个会话仅测试一个算法,参与者只能完成一个会话。我们在这里报告的数字与论文中数字不能直接比较,因为我们的地面实况图像的处理方式略有不同我们测试的参与者可能会有所不同。
FCN评分虽然感知研究可能是评估图形真实性的黄金标准,但我们也寻求一种不需要人体实验的自动定量测量。为此,我们采用的“FCN得分”,并用它来评估Cityscapes标签→照片任务。
FCN指标根据现成的语义分段算法(完全卷积网络,FCN)评估生成的照片的可解释性。 FCN预测生成的照片的标签映射。然后可以使用标准语义分段将该标签图与输入的地面实况标签进行比较,在测试时对512×512图像进行卷积运算。我们在实验中选择256×256,因为许多基线无法扩展到高分辨率图像,并且CoGAN无法完全卷积测试。
下面描述了这些指标。直觉是,如果我们从“汽车在路上”的标签图上生成照片,那么如果应用于生成的照片的FCN检测到“汽车在路上”,我们就成功了。
语义分段度量为了评估照片→标签的性能,我们使用来自Cityscapes基准测试的标准度量,包括每像素精度,每类精度和平均类别交叉联盟(Class IOU)

图 5:用于映射在城市景观图像上训练的标签照片的不同方法。
图6:在Google地图上映射航空照片地图的不同方法。从左到右:输入,BiGAN / ALI [7,9],CoGAN [32],特征丢失+ GAN,SimGAN [46],CycleGAN(我们的),pix2pix [22]训练配对数据和基础事实。
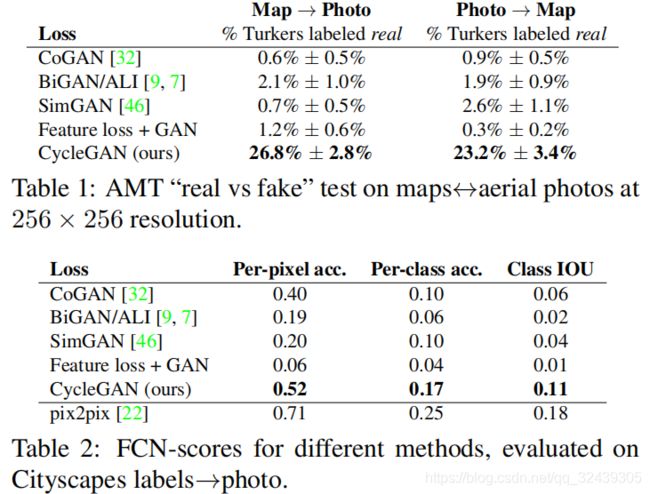
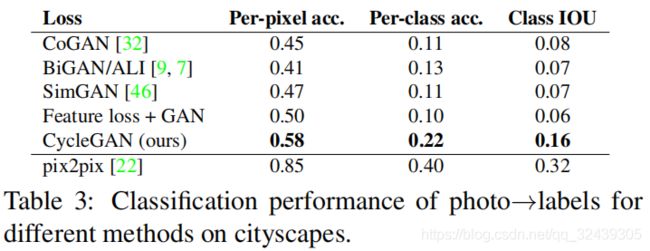

图 7:不同变量的定性分析。只加入Cycle,GAN等等,但最后CycleGAN的效果是最好的。GAN+forward和GANalone遭遇了模式坍塌问题。

图8:CycleGAN在“pix2pix”中使用的配对数据集上的示例结果,例如建筑标签↔照片和边缘↔鞋。

图9:身份映射(identity mapping loss)损失对莫奈的绘画→照片的影响。从左到右:输入绘画,没有身份映射丢失的CycleGAN,具有身份映射丢失的CycleGAN。身份映射丢失有助于预先输入输入绘画的颜色。
6 制约和结论
在颜色和纹理有明显变化的情况,CycleGAN能表现的非常好。但是有明显几何形状改变的情况,CycleGAN却很少成功。这可能是由于生成器结构导致的。对于一些有变化的图像,比如下面的普京老爷子骑在马上,CycleGAN就会表现的很糟糕。(哦,天哪,普京全身都是斑马纹身!)。
匹配图像和非匹配图像训练结果差异往往难以弥和。研究弱语义监督或许能改善这个状况。
看官看累了,麻烦点个喜欢吧。————店小二