机器学习第2集——回归决策树DecisionTreeRegressor() 附案例
先看看他在库中的类
class sklearn.tree.DecisionTreeRegressor (criterion=’mse’, splitter=’best’, max_depth=None,
min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None,
random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, presort=False)重要参数详解:
1、criterion :可选三种
① mse(均方误差,父节点和叶子节点之间的均方误差的差额将被用来作为特征选择的标准)
② friedman_mse(费尔德曼均方误差,标使用弗里德曼针对潜在分枝中的问题改进后的均方误差)
③ mae(绝对平均误差,使用叶节点的中值来最小化L1损失)
下面2-8个属性详见往期文章《机器学习第1集》
2、splitter
3、max_depth
4、min_samples_split
5、min_samples_leaf
6、max_features
7、random_state
8、min_impurity_decrease
重要属性:
1、feature_importances_
重要接口:
1、apply:
2、fit:用于导入数据集(训练集)
3、predict:
4、score:返回的是R²,可以为负,模型很糟糕的时候为负
建立模型还是三部曲:实例化、训练模型、评估模型
下面简单建立一颗回归树
# 先导入我们需要使用的库
# 使用环境是 jupyter notebook 或 jupyter lab
from sklearn.datasets import load_boston # sklearn.datasets为调用sklearn中自带的经典数据集
from sklearn.model_selection import cross_val_score # 导入给回归树评分的类
from sklearn.tree import DecisionTreeRegressor # 导入回归树模型regressor = DecisionTreeRegressor(random_state=0) # 实例化,其实就是建立模型的意思
# random_state=0 表示随机种子设为0
# 回归树的评价方法:交叉验证,cross交叉val验证score分数
cross_val_score(regressor # 输入模型
, boston.data # 输入特征矩阵
, boston.target # 输入目标矩阵
, cv=10 # 数据集分成10份进行交叉验证
# , scoring = 'neg_mean_squared_error' # 选择该项则模型得分以mse的负数形式返回
).mean() # 十次交叉验证求平均下面直接附案例,对(含有噪声的)正弦函数建立回归树
########################
# 导入库
########################
# 先导入需要的库
import numpy as np # 用于创建带有噪声的正弦函数的 一些点
from sklearn.tree import DecisionTreeRegressor # 导入回归树模型
import matplotlib.pyplot as plt # 用于作图
########################
# 创建一条带有噪声的正弦函数的一些点
########################
rng = np.random.RandomState(1) # 定义一个随机数种子
x = np.sort(5 * rng.rand(80,1), axis=0) # 产生一个80行1列的数组,将数组扩大5倍并排序
y = np.sin(x).ravel() # 利用上面的x生成y=sinx的数组,并将二维降成一维
y[::5] += 3 * (0.5 - rng.rand(16)) # 添加噪声
# 在y的值中,从头到尾的数值中,每5步作如下操作:
# 3*(0.5-(16个0到1之间的随机数))得到的值,赋值给y中对应的数值
# rand()方法是生成0到1之间的随机数,括号中可以填数字也可以填数组,例如rng.rand(10)、rng.rand(3,4)
# 把正弦函数图像画出来
plt.figure() # 创建画板
plt.scatter(x, y, s=20, edgecolor="black",c="darkorange", label="data") # scatter()用于画散点图
'''
plt.figure() 创建画板
figure(num=None, figsize=None, dpi=None, facecolor=None, edgecolor=None, frameon=True)
num:图像编号或名称,数字为编号 ,字符串为名称
figsize:指定figure的宽和高,单位为英寸;
dpi参数指定绘图对象的分辨率,即每英寸多少个像素,缺省值为80 1英寸等于2.5cm,A4纸是 21*30cm的纸张
facecolor:背景颜色
edgecolor:边框颜色
frameon:是否显示边框
'''
########################
# 建立模型三部曲
########################
# 实例化
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
# 训练模型
regr_1.fit(x, y)
regr_2.fit(x, y)
# 给模型评分
# 测试集导入模型,预测结果
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)
########################
# 画图
########################
plt.figure() # 创建画板/画布
plt.scatter(x, y, s=20, edgecolor="black",c="darkorange", label="data")
# s=图像的大小,edgecolor=边框颜色,c=点的颜色,label=标签
plt.plot(X_test, y_1, color="cornflowerblue",label="max_depth=2", linewidth=2)
# plt.plot()画折线图,其他参数都很好理解,自己看看
plt.plot(X_test, y_2, color="yellowgreen", label="max_depth=5", linewidth=2)
# 同上
plt.xlabel("data") # 横坐标标签
plt.ylabel("target") #纵坐标标签
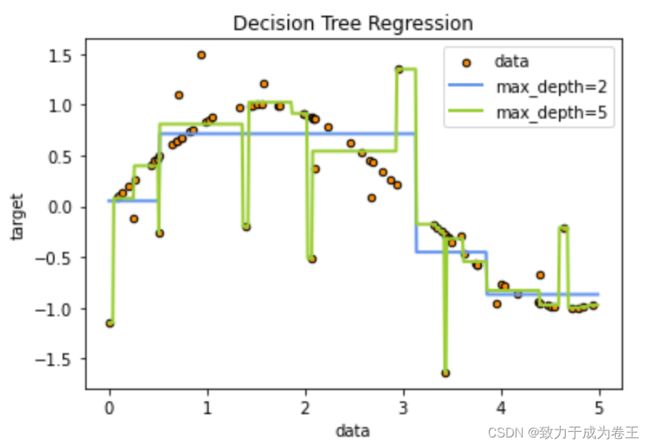
plt.title("Decision Tree Regression") #图的标题
plt.legend() #显示图例
plt.show() #把上面的代码的图画出来
得到的结果为: