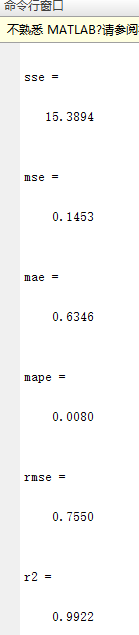高维多元数据拟合回归如何进行？？？

一、高维多元数据非线性/线性拟合：

Matlab绘制三维空间网格散点图，使用cftool工具箱实现三维空间绘图。cftool工具箱是应用程序中的Curve Fitting应用。选择拟合曲线的类型，工具箱提供的拟合类型有：
1) Custom Equations：用户自定义的函数类型。根据需求自行设定，但是有时候要根据实际数据情况设定，不然会出现偏差太大的问题，特别是对于实验结果数据拟合时，要根据变量与因变量之间的实际潜在趋势关系进行合理设定。
2) Exponential：指数逼近，有2种类型， aexp(bx) 、aexp(bx) + cexp(dx)
3) Fourier：傅立叶逼近，有7种类型，基础型是 a0 + a1cos(xw) + b1sin(xw)
4) Gaussian：高斯逼近，有8种类型，基础型是 a1exp(-((x-b1)/c1)^2)
5) Interpolant：插值逼近，有4种类型，linear、nearest neighbor、cubic spline、shape-preserving
6) Polynomial：多项式逼近，有9种类型，linear 、quadratic 、cubic 等
7) Power： 幂逼近，有2种类型，ax^b 、ax^b + c
8) Rational： 有理数逼近，分子、分母共有的类型是linear 、quadratic 、cubic 等此外，分子还包括constant型
9) Smoothing Spline： 平滑逼近
10) Sum of Sin Functions： 正弦曲线逼近，有8种类型，基础型是 a1sin(b1*x + c1)
拟合结果页面例子显示如下：




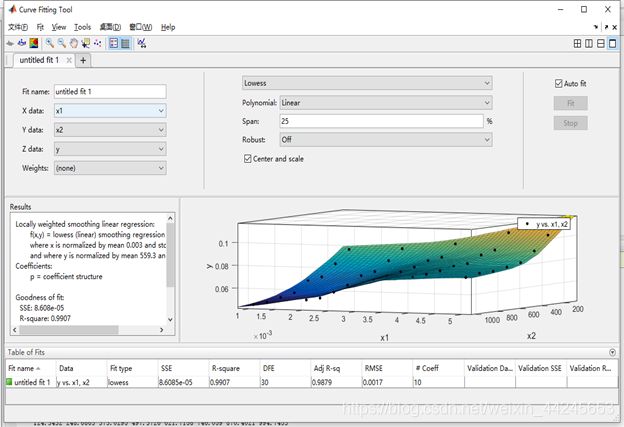
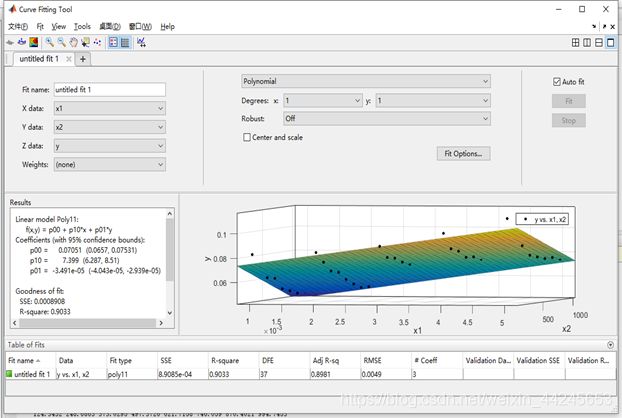
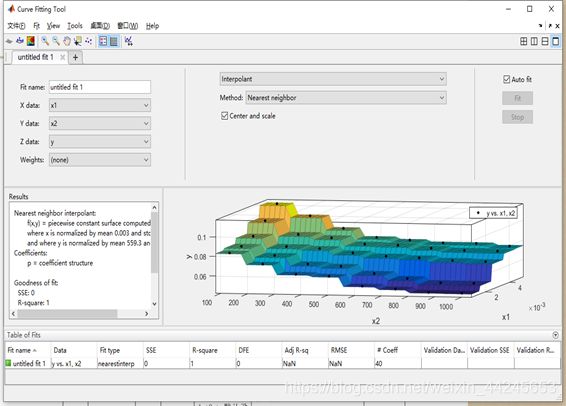
衡量其拟合结果的性能指标里面R-square 与 Adjusted R-square一个意思，通常看第一个，反映线性化拟合的好坏。SSE 与 RMSE 是标准差和均方差，意义也一样，反映拟合误差的好坏。SSE比R2重要，主要看SSE，R square为方程的确定系数，0~1之间，越接近1，表明方程的变量对因变量的解释能力越强。
但是对于多变量（3或者3个以上），该工具箱拟合出现问题， 无法拟合出最佳效果。经过查阅一些论坛和CSDN资料,解决方式有以下几种：
1、 用python加载KNN、Numpy、pandas、statsmodels等安装包进行算法求取，在迭代时会由于初值选定问题，出现结果偏差过大情况，需要不断根据经验调整相关参数。
2、 用1stOpt数据优化分析综合软件，对多维数据进行分析，求取最佳拟合参数。

二、1stOpt高维数据拟合

1stOpt是七维高科有限公司 （7D-Soft High Technology Inc.） 独立开发，拥有完全自主知识产权的一套数学优化分析综合工具软件包。以非线性回归为例，目前在该领域最有名的软件工具包诸如 Matlab, OriginPro, SAS, SPSS,DataFit, GraphPad 等，均需用户提供适当的参数初始值以便计算能够收敛并找到最优解。而1stOpt凭借其超强的寻优，容错能力，在大多数情况下 （大于90%) ，从任一随机初始值开始，都能求得正确结果。

2.1 1stOpt应用最优化算法包括：

1) Levenberg-Marquardt 法 (LM) + 通 用 全 局 优 化 算 法 (Universal Global Optimization - UGO)
2) Quasi-Newton 法(BFGS) + 通用全局优化算法(Universal Global Optimization- UGO)
3) 遗传算法 (Genetic Algorithms - GA)
4) 模拟退火 (Simulated Annealing - SA)
5) 下山单体法 (Simplex Method- SM) + 通用全局优化算法(Universal Global Optimization-UGO)
6) 离子群法 (Particle Swarm Optimization - PSO)
7) 最大继承法 (Max Inherit Optimization - MIO)
8) 差分进化法 (Differential Evolution - DE)
9) 自组织群移法 (Self-Organizing Migrating Algorithms - SOMA)
10) 共扼梯度法 (Conjugate-Gradient Method - CGM) + 通用全局优化算法(Universal Global Optimization - UGO)
11) 包维尔法 (Powell Optimization PO) + 通用全局优化算法(Universal Global Optimization UGO)
12) 禁忌搜索法 (Tabu Search -TS)
13) 单纯线性规划法 (Simplex Linear Program)

2.2 优化参数设置：

程序使用不同算法和相关参数设定进行多元高维数据拟合分析结果如下：

数据拟合效果分析评判标准（根据标准选定最优拟合参数）：
均方差RMSE 与 残差平方和SSE 越接近零
相关系数R: 1正相关 -1负相关
方程确定系数R-square: 越接近1，表示方程的变量对因变量的解释能力越强
决定系数DC: 越接近1
F-Statistic: 越大越好
通过上述对性能指标和迭代参数及时间的比较，得到最优拟合效果对应的最佳参数及相关实验参数因变量预测数据

三、Matlab多元高维数据拟合举栗~：

数据表格如下：

MATLAB参考程序如下：

clc;
clear;
close all;
filename='C:\Users\blue\Desktop\表五.xlsx';
A=xlsread(filename);
x_1=A(1:27,1);
x_2=A(1:27,2);
x_3=A(1:27,3);
x_4=A(1:27,4);
x_5=A(1:27,5);
x_6=A(1:27,6);
%x_7=A(1:27,7);
%x_8=A(1:27,8);
%x_9=A(1:27,9);
%x_10=A(1:27,10);
%x_11=A(1:27,11);
%x_12=A(1:27,12);
y_1=A(1:27,7);
x=[1:1:27];
% % % % % % y_2=-1029 + 9.7*x_1 - 29*x_2 + 333*x_3 + 13.9*x_4 - 0.35*x_5 + 26.3 *x_6 - 0.001 *x_1.*x_1 + 39.6*x_2.*x_2+ 2.8*x_3.*x_3 - 7.84*x_4.*x_4 + 0.00015*x_5.*x_5 - 0.103*x_6.*x_6 - 0.0142*x_1.*x_5 - 0.177*x_1.*x_6+ 0.071*x_2.*x_5 - 2.22*x_2.*x_6 + 0.280*x_3.*x_5 - 7.8*x_3.*x_6 - 0.0032*x_4.*x_5 + 0.169*x_4.*x_6+ 0.000012*x_1.*x_5.*x_5 + 0.00106*x_1.*x_6.*x_6 - 0.000261*x_3.*x_5.*x_5 + 0.0355*x_3.*x_6.*x_6;

y_5=-5633-65.37*x_1 + 4810*x_2 + 55.42*x_3 - 92.00*x_4 + 8.764*x_5 - 40.00*x_6 + 0.9142*x_1.*x_1- 821.1*x_2.*x_2 + 13.71*x_3.*x_3 + 24.84*x_4.*x_4 - 0.001255*x_5.*x_5 + 0.02084*x_6.*x_6 - 0.3265*x_1.*x_5+ 1.918*x_1.*x_6 - 0.1611*x_2.*x_5 - 0.3082*x_2.*x_6 - 1.253*x_3.*x_5 - 0.8958*x_3.*x_6 + 0.004360*x_4.*x_5- 0.1193*x_4.*x_6 + 0.002851*x_1.*x_1.*x_5 - 0.02387*x_1.*x_1.*x_6 + 0.002910*x_1.*x_2.*x_5+ 0.02869*x_1.*x_3.*x_5 + 0.000027*x_1.*x_5.*x_5 + 0.000101*x_3.*x_5.*x_5;

%y_5=-3785+ 49.00*x_1 + 612.8*x_2-108.0*x_3+52.54*x_4-0.2229*x_5 + 4.420*x_6 + 1.672*x_7+ 56.20*x_8 - 0.2725*x_1.*x_1 - 74.13*x_2.*x_2 + 50.99*x_3.*x_3 - 13.41*x_4.*x_4 + 0.000617*x_5.*x_5+ 0.01308*x_6.*x_6 - 0.000701*x_7.*x_7 - 0.4724*x_8.*x_8 - 0.01444*x_1.*x_5 - 0.03356*x_1.*x_6- 0.02295*x_1.*x_7 - 0.1039*x_1.*x_8 + 0.01925*x_2.*x_5 - 2.052*x_2.*x_6 - 0.06478*x_2.*x_7+ 1.079*x_2.*x_8 + 0.003167*x_3.*x_5 - 1.837*x_3.*x_8;
% A=y_1-y_2;

%y_5=53.21 - 3.437*x_1 - 91.63*x_2 + 79.41*x_3 - 6.399*x_4 + 0.03888*x_5 - 1.609*x_6 - 0.1323*x_7- 0.3045*x_8 + 0.07099*x_9 + 4.540*x_10 + 0.04064*x_1.*x_1 + 7.256*x_2.*x_2 - 20.10*x_3.*x_3+ 1.986*x_4.*x_4 - 0.000046*x_5.*x_5 + 0.000751*x_6.*x_6 + 0.000035*x_7.*x_7 + 0.01215*x_8.*x_8+ 0.000024*x_9.*x_9 - 0.03098*x_10.*x_10 + 0.006823*x_2.*x_5 + 0.4939*x_2.*x_6 + 0.03567*x_2.*x_7- 0.3303*x_2.*x_8 - 0.03917*x_2.*x_9 + 0.2129*x_2.*x_10;

%y_5=-1725 - 4.911*x_1 + 746.6*x_2 + 146.2*x_3 + 16.09*x_4 - 0.06363*x_5 + 0.4992*x_6 - 0.03373*x_7+ 18.87*x_8 - 0.01789*x_9 - 5.917*x_10 + 1.905*x_11 - 1.191*x_12 - 0.2857*x_1.*x_1 - 128.8*x_2.*x_2- 36.46*x_3.*x_3 - 2.824*x_4.*x_4 + 0.000040*x_5.*x_5 - 0.001777*x_6.*x_6 + 0.000062*x_7.*x_7- 0.1723*x_8.*x_8 + 0.000015*x_9.*x_9 + 0.03393*x_10.*x_10 - 0.002469*x_11.*x_11 + 0.000556*x_12.*x_12+ 0.03107*x_1.*x_11 + 0.01863*x_1.*x_12;


%figure(5);

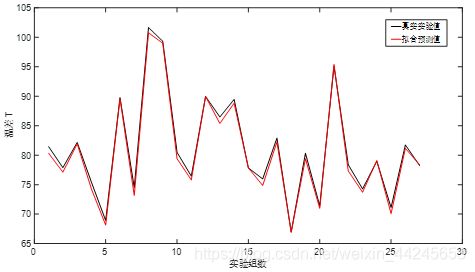
plot(x,y_1,'k',x,y_5,'r','linewidth',3);    
xlabel('实验组数','FontSize',20);
ylabel('温差T','FontSize',20);
legend('真实实验值','拟合预测值')



sse = sum((y_1 - y_5).^2);%残差平方和(SSE)
mse = sqrt(sum((y_1 - y_5).^2)) ./ 27;%均方误差（MSE）
mae = mean(abs(y_1 - y_5));%平均绝对误差（MAE）
mape = mean(abs((y_1 - y_5)./y_1));%平均绝对百分比误差（MAPE）
rmse = sqrt(mean((y_5 - y_1).^2));%均方根误差（RMSE）
r2 = 1 - (sum((y_5-y_1).^2) / sum((y_1 - mean(y_1)).^2));%决定系数（R2-R-Square）
sse,mse,mae,mape,rmse,r2

运行的结果如下：

3.1 定性分析

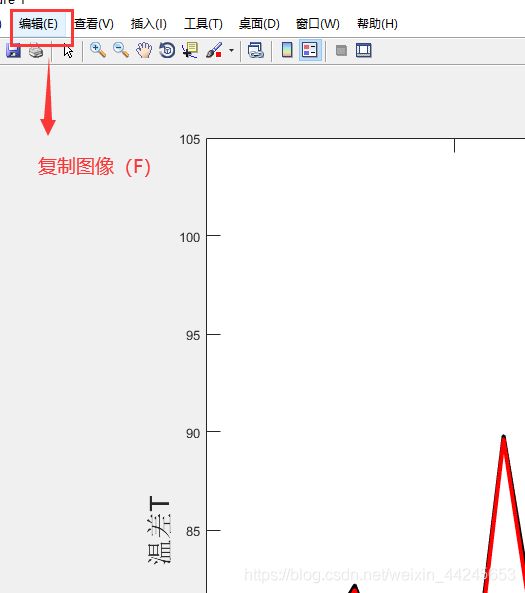
在matlab导出图像的时候，默认设置分辨率不够，需要对导出进行设置：

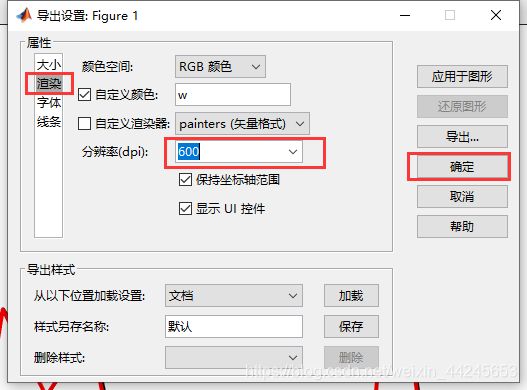
3.2 定量分析

误差类（越小越好，一般是近0）：
均方差（RMSE）
残差平方和（SSE）
均方误差（MSE）
平均绝对误差（MAE）
平均绝对百分比误差（MAPE）近0%越好！完美模型~
其他：
相关系数R: 1正相关 -1负相关
决定系数（R2-R-Square）: 越接近1，表示方程的变量对因变量的解释能力越强
决定系数DC: 越接近1
F-Statistic: 越大越好

四、python多元高维数据拟合举栗~：

此处以线性为例：

4.1 主成分分析前

python参考如下：
这个例子是用Kaggle的云服务器跑的，本地PC也可进行(但要配置好相关安装包)~~
表格导入：

python程序：

import numpy as np
import pandas as pd
import statsmodels.api as sm
# import matplotlib.pyplot as plt

file = r'../input/data3333/data2(1).csv'
data = pd.read_csv(file)
data.columns = ['y', 'x1', 'x2', 'x3', 'x4', 'x5', 'x6'

x = sm.add_constant(data.iloc[:,1:]) #生成自变量
y = data['y'] #生成因变量
model = sm.OLS(y, x) #生成模型
result = model.fit() #模型拟合
print(result.summary()) #模型描述

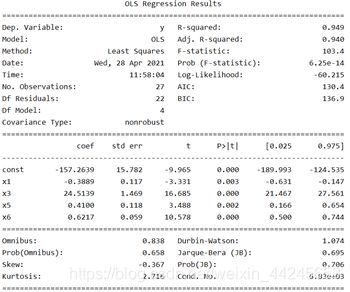
通过对自变量x1、x2、x3、x4、x5、x6与应变量进行OLS建模，模型参数指标如下图所示。得到的回归函数：
y1=-164.5417-0.3889x1+1.0556x2+25.6852x3+0.937x4+0.41x5+0.6217x6
没有对成分进行分析的模型运行结果：

4.2 主成分分析后

由于此时建立的回归模型的精度不够高，故需要对其进行主成分分析。由于x2的 P>|t| 值为0.723，远远大于其他自变量的值，所以去掉自变量x2之后再进行建模，同时设置 P>|t| 的阈值为0.05后去掉了自变量x4，所得模型参数如下图所示。（设置P>|t|的阈值通常为0.05、0.02、0.01）

def looper(limit):
    cols = ['x1', 'x3', 'x5', 'x6']
    for i in range(len(cols)):
        data1 = data[cols]
        x = sm.add_constant(data1) #生成自变量
        y = data['y'] #生成因变量
        model = sm.OLS(y, x) #生成模型
        result = model.fit() #模型拟合
        pvalues = result.pvalues #得到结果中所有P值
        pvalues.drop('const',inplace=True) #把const取得
        pmax = max(pvalues) #选出最大的P值
        if pmax>limit:
            ind = pvalues.idxmax() #找出最大P值的index
            cols.remove(ind) #把这个index从cols中删除
        else:
            return result
 
result = looper(0.05)
result.summary() #模型描述

运行结果如下：

再进行定性分析：
未进行主成分分析： y1=-164.54170.3889x1+1.0556x2+25.6852x3+0.937x4+0.41x5+0.6217x6
进行主成分分析后： y2=-157.26390.3889x1+24.5139x3+0.41x5+0.6217x6

主成分分析前后的真实实验值与拟合预测值对比如下图所示：


如上图可以看出，经过主成分分析之后，去掉了无关自变量的影响 （不能决绝地说这两自变量对输出没有贡献，只能说贡献度很小） ，拟合精度稍有下降，但是在实际工程项目应用中，这种情况是比较常见的，但整体流程是没有什么问题的！

五、数据归一化

上述分析过程没有做数据归一化，但是在实际任务中，这个过程是非常有必要的，因为自变量一旦过多的话，自变量相互之前可能联系并不大，而且单位不统一，数据归一化主要起到统一量纲的作用！！！
数据归一化过程：
一般是将数值统一到 （0，1） 或 （-1，1）。
例如：X1=10，20，30，40，50. 归一化 0-1 之间。统一如公式（5-1）所示：

$$f(x)=(x-x_{min})/(x_{max}-x_{min})\text{\hspace{1em}(5.1)}$$
其中，可以理解如下：最小的10看作0，最大的50看作1，那么中间的数值比如20就可以归一化为0.25，如公式(5-2)所示：
$$f(x)=(20-10)/(50-10)=1/4=0.25\text{\hspace{1em}(5.2)}$$

以上内容如有错误，还望各位大神指教一二噢！比心~~~！！！
整理总结不易，还望给个关注和一键三连，欢迎各位大可爱点赞、关注、收藏和转发~