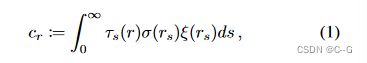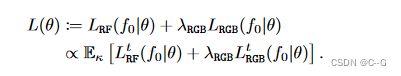75、DiffRF: Rendering-Guided 3D Radiance Field Diffusion
简介
主页:https://sirwyver.github.io/DiffRF/
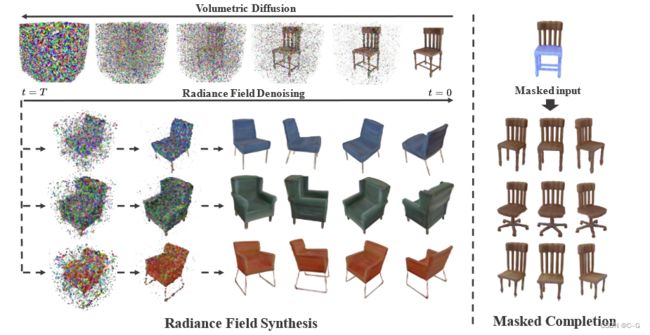
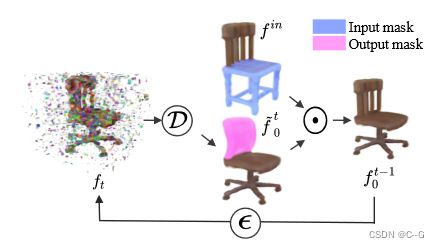
对应用于三维亮度场的概率扩散过程进行去噪。在3D监控和体积渲染的指导下,模型能够无条件地合成高保真3D资产(左)。
蒙面补全的新应用(右),即从不完整的对象中恢复形状和外观的任务(在右上方的椅子上用浅蓝色突出显示),由模型作为条件推理解决,无需特定任务训练
基于去噪扩散概率模型的三维辐射场合成新方法,提出了一个三维去噪模型,该模型直接作用于显式体素网格表示,但是,由于从一组摆拍图像生成的辐射场可能是模糊的,并且包含伪影,因此难以获得真实辐射场样本,通过将去噪公式与渲染损失配对来解决这一挑战,使模型能够学习一个偏向于良好图像质量的偏差先验,而不是试图复制拟合错误.
贡献点:
- 引入了第一个扩散模型,可以直接在3D辐射场上操作,实现高质量、真实的3D几何和图像合成。
- 三维亮度场掩模补全的新应用,它可以理解为图像修补在体积域的自然扩展
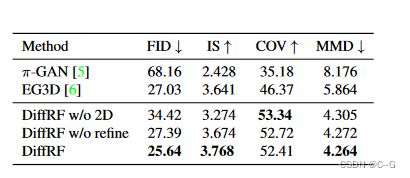
- 在无条件和条件设置中展示了令人信服的结果,例如,在具有挑战性的PhotoShape Chairs数据集上,通过改进基于gan的图像质量(FID从27.03提高到25.64)和几何合成(将MMD从5.86提高到4.26)的方法
实现流程
方法由3D对象的生成模型组成,该模型建立在最近最先进的扩散概率模型,通过注入不同尺度的噪声来恢复一个逐渐损坏3D对象的过程,3D对象被表示为辐射场,因此学习的去噪过程允许方法从噪声中生成对象辐射场
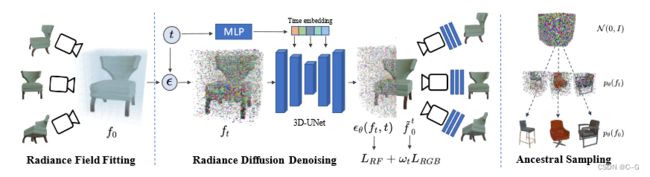
对于从1,…, T均匀采样的时间步长 t,首先根据一个固定的噪声时间表扩散一个初始辐射场 f 0 f_0 f0 。得到的 f t f_t ft 通过一个有时间条件的3D-UNet,给出应用噪声 ε ε ε 的估计值。通过噪声预测损失 L R F L_{RF} LRF 以及预测去噪 f ~ 0 \tilde{f}_0 f~0 上的渲染损失 L R G B L_{RGB} LRGB来指导模型。
扩散模型
扩散模型原理公式参考
Generation process
去噪过程首先从标准多元正态分布 p ( f T ) : = N ( f T ∣ 0 , I ) p(f_T) :=\Nu(f_T | 0, I) p(fT):=N(fT∣0,I) 中采样状态 f T f_T fT,并通过利用具有学习参数 θ 的高斯分布的反向跃迁概率 p θ ( f t − 1 ∣ f t ) p_θ(f_{t−1}| f_t) pθ(ft−1∣ft) 从 f t f_t ft 中生成状态 f t − 1 f_{t−1} ft−1
![]()
生成过程迭代到最终状态 f 0 f_0 f0,它表示由方法生成的3D对象的亮度场,考虑对(3)中高斯分布的均值进行下面的重参数化
![]()
其中 ε θ ( f t , t ) ε_θ(f_t, t) εθ(ft,t) 是神经网络预测的用于破坏 f t − 1 f_{t−1} ft−1 的噪声,而 a t a_t at 和 b t b_t bt 是预定义的系数,协方差 Σ t Σ_t Σt 采用预定义值,尽管它可能与数据相关
Diffusion process
扩散过程由离散时间马尔可夫链控制,其状态空间和时间边界与生成过程中提到的相同,但具有预先定义并给出的高斯转移概率
![]()
α t : = 1 − β t , 0 ≤ β t ≤ 1 \alpha_t := 1-\beta_t,0 \leq \beta_t \leq 1 αt:=1−βt,0≤βt≤1
使用 f 0 f_0 f0 推导 f t f_t ft
![]()
α ˉ t : = ∏ i = 1 t α i \bar{\alpha}_t := \prod^t_{i=1}\alpha_i αˉt:=∏i=1tαi
loss
损失 L R F L_{RF} LRF,用于惩罚不符合数据分布的辐射场的生成
损失 L R G B L_{RGB} LRGB,用于提高生成的辐射场的渲染质量
L R F L_{RF} LRF
从负对数似然(NLL)的变分上界开始推导出模型的训练目标,这个上限需要指定一个替代分布,称之为 q,因为它确实对应于控制扩散过程的分布 q,与生成过程建立了预期的基本联系,数据点 f 0 ∈ F f_0∈F f0∈F 的NLL可以通过利用 q 得到上界
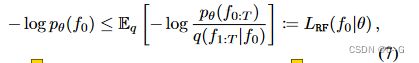
其中 f t 1 : t 2 f_{t_1:t_2} ft1:t2 代表( f t 1 f_{t_1} ft1,…, f t 2 f_{t_2} ft2),包围NLL的损耗 L R F ( f 0 ∣ θ ) L_{RF}(f_0|θ) LRF(f0∣θ) 可以进一步分解为下面的和,直到一个与 θ 无关的常数
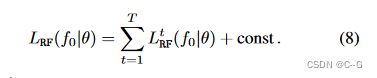
直观来看
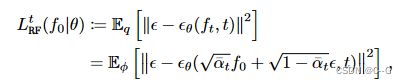
φ ( ε ) : = N ( ε ∣ 0 , I ) φ(ε) := N (ε|0, I) φ(ε):=N(ε∣0,I) 为高斯分布
l R G B l_{RGB} lRGB
用一个额外的 RGB 损失 L R G B ( f 0 ∣ θ ) L_{RGB}(f_0|θ) LRGB(f0∣θ) 来弥补先前的损失,旨在提高生成的辐射场的渲染质量。事实上,一旦尝试渲染辐射场,在之前的损失中隐含地用于评估生成的辐射场的质量的表示上的欧氏度量并不一定确保没有伪影。
将 L R G B ( f 0 ∣ θ ) L_{RGB}(f_0|θ) LRGB(f0∣θ) 定义为与(8)相似的时间特异性项 L R G B t ( f 0 ∣ θ ) L^t_{RGB}(f_0|θ) LRGBt(f0∣θ) 的和
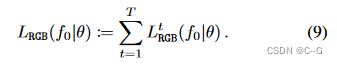
给定一个辐射场 f ∈ F f∈F f∈F和一个视点 v,用R(v, f)表示用公式(1)从视点v 渲染 f 后得到的图像,用 ℓ v ( f , f ′ ) ℓ_v(f, f ') ℓv(f,f′) 表示使用辐射场从视点v 渲染图像 f 和 f’ 之间的欧氏距离
![]()
这个想法是比较从数据分布中采样的给定亮度场 f 0 f_0 f0 的渲染,与用 t 扩散步骤损坏的相同亮度场,然后完全去噪
从 q ( f t ∣ f 0 ) q(f_t|f_0) q(ft∣f0) 中采样第一个 f t f_t ft,然后从 p θ ( f 0 ∣ f t ) p_θ(f_0|f_t) pθ(f0∣ft) 中采样 f 0 f_0 f0
从 L R F t L^t_{RF} LRFt 的定义来看,损失趋向于 ε ≈ ε θ ( f t , t ) ε≈ε_θ(f_t, t) ε≈εθ(ft,t),从中可以得出近 f ~ 0 t ( ε , θ ) : = f 0 + 1 − α ˉ t α ˉ t ( ε − ε θ ( f t , t ) ) \tilde{f}^t_0(ε,θ):= f_0 + \frac{\sqrt{1-\bar{\alpha}_t}}{\sqrt{\bar{\alpha}_t}}(ε - ε_θ(f_t,t)) f~0t(ε,θ):=f0+αˉt1−αˉt(ε−εθ(ft,t))
![]()
对于视点 v 和 ε φ ( ε ) ε ~ φ(ε) ε φ(ε),期望是关于先验分布 ψ 的,因为只有当阶跃 t 接近于零时,近似才是合理的,所以引入了一个权重 w t w_t wt,它随着阶跃值的增加而衰减(例如,使用 ω t : = ˉ α ˉ t 2 ω_t:=̄\bar{\alpha}_t^2 ωt:=ˉαˉt2)
Final loss
部分补全
为了适应特定的任务,需要训练GANs,而扩散模型可以在测试时有效地适应。利用这一特性来完成掩模辐射场补全的新任务。
将两者结合在掩膜亮度场补全的新任务中:给定一个亮度场和一个3D掩膜,合成一个与非掩膜区域协调的掩膜区域补全,通过逐步引导已知区域的无条件采样过程到输入 f i n f^{in} fin 来执行条件补全
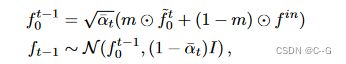
m 是应用于输入的二进制掩码,⊙表示在体素网格上逐元素的乘法
实验
选取时刻总数为 T = 1000,扩散过程的方差从 β 1 = 0.0015 \beta_1 = 0.0015 β1=0.0015增加到 β T = 0.05 \beta_T = 0.05 βT=0.05, L R G B t L^t_{RGB} LRGBt的权重 ω t : = ˉ α ˉ t 2 ω_t:=̄\bar{\alpha}_t^2 ωt:=ˉαˉt2

Limitations
虽然方法在条件和无条件辐射场合成的任务中显示出有希望的结果,但仍然存在一些局限性。与基于gan的方法相比,采样时间明显更长。在这种情况下,探索利用更快的采样方法会很有趣。最后,模型受到训练时间内存限制的最大网格分辨率的约束。这些问题可以通过探索因子化神经场表示来解决。