论文阅读23 - Mixture Density Networks(MDN)混合密度网络理论分析
Mixture Density Networks
最近看论文经常会看到在模型中引入不确定性(Uncertainty)。尤其是MDN(Mixture Density Networks)在World Model这篇文章多次提到。之前只是了解了个大概。翻了翻原版论文和一些相关资料进行了整理。
1. 直观理解:
混合密度网络通常作为神经网络的最后处理部分。将某种分布(通常是高斯分布)按照一定的权重进行叠加,从而拟合最终的分布。
如果选择高斯分布的MDN,那么它和GMM(高斯混合模型 Gaussian Mixture Model)有着相同的效果。但是他们有着很明显的区别:
-
MDN的
均值、方差、每个模型的权重是通过神经网络产生的,利用最大似然估计作为Loss函数进行反向传播从而确定网络的权重(也就是确定一个较好的高斯分布参数) -
GMM的
均值、方差、每个模型的权重是通过估计出来的,通常使用EM算法来通过不断迭代确定。GMM的详解以及为什么要用EM而不是极大似然估计来优化参数,请见这个博客
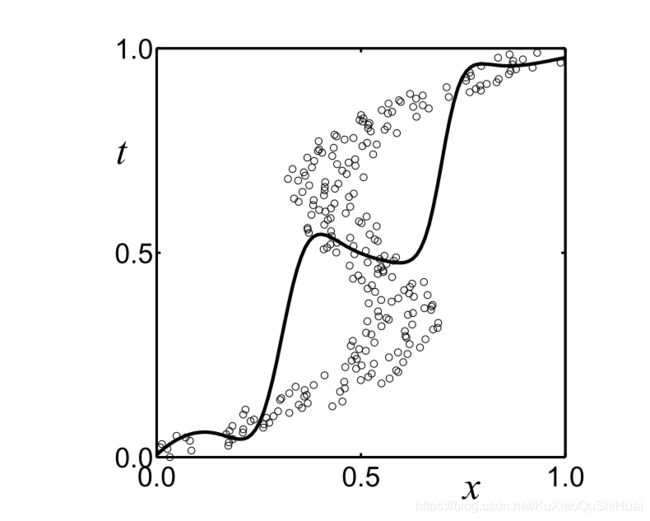
总之,MDN的思想与GMM一样,将模型混合的思想与神经网络相结合。在回归问题上通常都有很好的表现。例如,论文中提到的一个翻转的x,t翻转的例子:
-
普通的神经网络,使用sum-of-squares error作为loss可以得到一个较好的拟合效果。
-
同样的数据,将x和t的数据翻转(原来x的数据作为标签,原来t的数据作为训练集,
tmp = x, x = t, t = tmp):使用sum-of-squares error作为loss似乎并没有捕捉到我们的走势。
-
MDN效果如何呢
先上效果图(来自原版论文)。下图绘制的是可能性最大的点(分布的均值)。可见基本上可以捕捉到这个趋势。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oPgn4RpM-1605340386543)(Untitled.assets/image-20201114140657278.png)]
在输出的分布内进行采样获取预测,图片来自:
2. 算法细节
2.1. 结构
参数化表示:
C C C :要混合的分布个数。是用户需要制定的参数。例如我们需要混合5个高斯分布作为最终结果,那么C = 5;
α \alpha α :每个分布的权重参数。网络输出的参数
D D D: 某一种被混合的分布, 如果是高斯分布,那么KaTeX parse error: Undefined control sequence: \cal at position 1: \̲c̲a̲l̲ ̲D 就应该用 N N N表示。
λ \lambda λ:分布的一些参数,高斯分布则包括 μ \mu μ和 σ \sigma σ。网络输出的参数
需要注意的是:混合的分布可以是任意的。
以高斯分布为例,网络结构如下:
- α \alpha α (alpha)的和应该等于1,即 ∑ c C α c = 1 \sum^{C}_{c} \alpha_c = 1 ∑cCαc=1。 所以我们可以在使用softmax激活函数来解决。
- σ \sigma σ(sigma)>0。 可以保证这个的方法有很多,在Mixture Density Networks中使用指数激活: σ = e x p ( z ) \sigma = exp(z) σ=exp(z)。指数可能会引起数值不稳定,出现无穷大。可以使用变种的ELU [3],即 σ = E L U ( σ ) + 1 \sigma = ELU(\sigma)+1 σ=ELU(σ)+1
- μ \mu μ 的范围是否要确定区间,可以根据实际问题。例如价格预测,不可能出现负的,就可以选择相关的激活函数来固定区间大于0.
2.2 Loss设计:
损失函数使用的极大似然估计。极大似然估计认为我们采样出来的都是那些出现概率最大的数。所以我们希望我们需要最大化的似然函数为(这里使用了平均值,即每个分布的似然函数大小):
极大似然估计公式: L ( θ ) = L ( x 1 , x 2 . . . x n ; θ ) = ∏ i = 1 n p ( x i ; θ ) L(\theta) = L(x_1,x_2...x_n ; \theta) = \prod_{i = 1 } ^n p(x_i; \theta) L(θ)=L(x1,x2...xn;θ)=∏i=1np(xi;θ)。用多个分布混合,则 p ( x i ; θ ) = ∑ k K a k p k ( x i ; θ ) p(x_i;\theta) = \sum_k ^K a_k p_k(x_i ; \theta) p(xi;θ)=∑kKakpk(xi;θ)。 下式中 x i x_i xi为 y n ∣ x n y_n|x_n yn∣xn
L ( θ ) = 1 N ∏ n N ∑ k K a k p k ( y n ∣ x n ) l n ( L ( θ ) ) = 1 N ∑ n N log { ∑ k K α k p k ( y n ∣ x n ) } L(\theta) = \frac{1}{N} \prod_n ^N \sum_k ^K a_k p_k(y_n|x_n) \\ ln(L(\theta)) =\frac{1}{N} \sum_n ^N \log \{ \sum_k ^K \alpha_k p_k(y_n|x_n)\} L(θ)=N1n∏Nk∑Kakpk(yn∣xn)ln(L(θ))=N1n∑Nlog{k∑Kαkpk(yn∣xn)}
N 样本总数
K 分布的数量
a k a_k ak 是当前分布的权重
p k p_k pk 是当前分布的概率
$ \sum_k ^K a_k p_k(y_n|x_n)$ 就是 x n x_n xn样本出现的概率。对应似然函数中的 p ( x i ; θ ) p(x_i; \theta) p(xi;θ)。 是k个分布按照权重 α \alpha α累加的结果。
优化器一般都是梯度下降,用来最小化目标函数,所以我们要在上式加一个负号,作为优化函数,这样就是梯度上升最大化上式。
L o s s ( θ ) = − l n ( L ( θ ) ) Loss(\theta) = -ln(L(\theta)) Loss(θ)=−ln(L(θ))
如果是N个高斯分布,那么我们的损失函数:
L o s s ( θ ) = − 1 N ∑ 1 N log { ∑ k α k N ( y n ∣ μ k , σ k 2 ) } Loss(\theta) = -\frac{1}{N} \sum_1 ^N \log \{\sum_k \alpha_k N(y_n|\mu_k,\sigma^2_k)\} Loss(θ)=−N11∑Nlog{k∑αkN(yn∣μk,σk2)}
N ( y ∣ μ , σ 2 ) = 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2 N(y|\mu,\sigma^2) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{\frac{-(x-\mu)^2}{2\sigma^2}} N(y∣μ,σ2)=2πσ21e2σ2−(x−μ)2
3. 总结
MDN实现简单,而且可以直接模块化的连接到神经网络的后端。他的结果可以得到一个概率范围,相对有deterministic类只输出一个结果,往往有更好的健壮性。[3][4]中有相关代码实现。
4. reference:
[1]. Christopher M. Bishop, Mixture Density Networks (1994)
[2]. Blog-详解EM算法与混合高斯模型(Gaussian mixture model, GMM)
[3]. Blog-A Hitchhiker’s Guide to Mixture Density Networks
[4]. Blog-Mixture Density Networks