因果推理学习笔记（一）

因果推理（Causal Inference）：Inferring the enfects of any treatment/policy/intervention/etc.
因果推理就是推断一个事物对另一个事物的影响。

1. 辛普森悖论说（Simpson’s paradox）

当人们尝试探究两种变量是否具有相关性的时候，会分别对之进行分组研究。然而，在分组比较中都占优势的一方，在总评中有时反而是失势的一方。

以下是一个辛普森悖论的例子。

存在一种疾病，患病人的状况分两种，该病的治疗方式有两种，治疗结果有两种：

• new disease: COVID-27
• Treatment T: A(0) and B(1)
• Condition C: mild(0) or severe(1)
• Outcome Y: alive(0) or dead(0)
• 假设: B比A稀缺

下表是两种治疗方式治疗时的死亡率：

而如果将数据按照Condition分组，死亡率为：

从上图可以看出，不管是mild的情况还是severe的情况，用B方式治疗时的死亡率都是比A小的，但从整体来看的话，B方式治疗的死亡率却比A高。这就是辛普森悖论。

解释：A的整体死亡率，也就是16%这个数字是这样得来的：

$\frac{1400}{1500}\times 0.15+\frac{100}{1500}\times 0.30=0.16$

而B的整体死亡率，也就是19%这个数字是这样得来的：

$\frac{50}{550}\times 0.10+\frac{500}{550}\times 0.20=0.19$

在计算A的整体死亡率时，轻症患者的死亡率（0.15）占了很大的权重，而计算B的整体死亡率时，重症患者的死亡率（0.20）占了很大的权重。这样的计算过程是不平等的，这就导致了在分组比较时B占优势，而在整体评价中B处于劣势。

若要从A、B中选择一个的话，从不同的角度考虑会有不同的结论。

（1）选择A
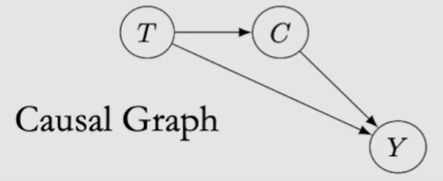
选择B是因为我假设因果图如下：

在这个因果图中，Condition是治疗方式的原因。也就是说，不同的治疗方式适用于不同的病况。当病况轻微时，为了不占用B这一稀缺治疗方式，医生会使用A方案为其治疗；当病况严重时，才使用B来治疗。因此在表格中可以看到，A治疗的患者大多为轻状，B治疗的患者大多为重状。从这个角度考虑的话，方案B是更好的，我们肯定希望使用方案B来治疗这种疾病。

（2）选择B
选择A是因为假设因果图如下：

在这个因果图中，Treatment是Condition的原因。意思是说，如果你选择B作为治疗方式，而B是非常稀缺的，你可能需要等很久才会得到真正的治疗，而在等待这个过程中，你的病情会从mild转为severe，这也是B治疗的大部分患者都是重症患者的原因。但如果选择A的话，就不需要等待，可以得到及时的治疗，症状就可能不会加重而会治愈。所以从这个角度才看的话，A是最佳选择。

2. 关联不意味着因果

以“穿鞋睡觉与头痛醒来的关联”为例。

统计发现，如果穿着鞋子睡觉的话，有很大的概率醒来的时候会头痛。这会让人们觉得，穿着鞋睡觉会导致醒来的时候头痛。然而，穿鞋睡觉和醒来头痛之间并没有因果关系。

这是因为，其实一个人穿鞋睡觉的话，这个人大概率之前喝了酒。

我们前面之所以会得出错误的结论，是因为confounding，睡前喝酒这个因素混淆了穿鞋睡觉对醒来是否头痛的影响。我们得到的关系其实是混杂关系和因果关系的混合。

3. 什么意味着因果？

既然关联不意味着因果，那什么才意味着因果呢？

引入一个概念：potential outcomes（潜在结果）。看一个例子:

我现在头痛，我有一种药。如果我吃了药，头痛好了，那我就会得出结论，这种药对头痛有效。但如果我没吃药我的头痛也好了，我可能会认为，这种药对头痛无效。针对我吃药或是不吃药的情况，我的头痛好或是不好就是潜在结果。

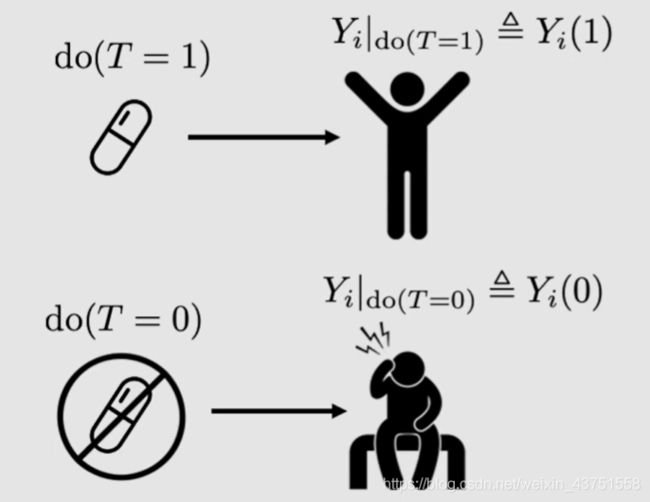
如上图，$Y_i(1)$代表吃药的潜在结果，$Y_i(0)$代表不吃药的潜在结果，那么吃药的因果效应就是潜在因果之间的差异：

但是现在有一个问题是，如果我吃了药，我可以观察到吃药的潜在结果$Y_i(1)$，但我没法观察到不吃药的潜在结果$Y_i(0)$，所以我没法计算因果效应。同样的，我不吃药的情况，没办法得到$Y_i(1)$，也无法计算因果效应。

一个方法是对我多次吃药或不吃药观察到的潜在结果进行平均，计算药物的平均治疗效果：

$E[Y_i(1)-Y_i(0)]=E[Y(1)]-E[Y(0)]$

但是这并不等于我在不同情况下观察到的结果的差异：

$E[Y_i(1)-Y_i(0)]=E[Y(1)]-E[Y(0)]\ne E[Y|T=1]-E[Y|T=0]$

原因是关联不意味着因果。我头痛是吃药的原因，所以会存在混杂关系，上式最右边的式子实际上是混淆关系和因果关系的混合。

为了去除混杂关系，可以做随机对照试验。对于一批人，为每个人随机地决定吃药或不吃药，观察他们的潜在结果。这样得到的潜在结果就不会有任何混杂因素的干扰，因为吃药或不吃药都是随机的。

4. 观察研究中的因果

随机对照实验是得到因果关系的一种方法，但这种实验有时候会受到道德约束而不可行，有时候甚至不可能做这样的实验。因此观察研究是很重要的。

在观察研究中，为了得到因果关系，需要调整或控制干扰因子。

用W表示混杂因素，则在存在混杂关系的时候：

通过对上式中的W进行边缘化（marginalize），就可以实现随机化T从而得到没有混杂因素的因果关系：

知识补充：边缘概率（又称先验概率）是某个事件发生的概率。边缘概率是这样得到的：在联合概率中，把最终结果中那些不需要的事件通过合并成它们的全概率，而消去它们（对离散随机变量用求和得全概率，对连续随机变量用积分得全概率），这称为边缘化（marginalization）。

回到一开始的COVID-27的例子，可以用上面的公式计算因果效应了。下面只考虑Condition是Treatment的原因的情况。

由于这里的干扰因子W是C，而且是有两个取值的离散变量，因此可以将公式写为：

那么就可以得到A的因果效应：

$\frac{1450}{2050}\times 0.15+\frac{600}{2050}\times 0.30=0.194$

B的因果效应：

$\frac{1450}{2050}\times 0.10+\frac{600}{2050}\times 0.20=0.129$

用这种计算方式，同种Conditon下A和B的权重相同，因此计算过程是公平的，不存在混淆因素的，计算结果可以看作因果关系的结果。