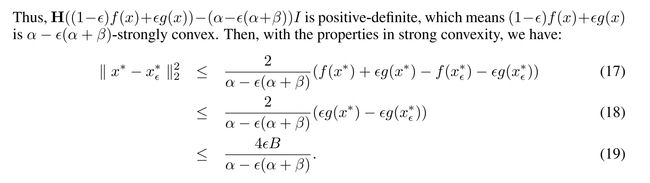Bert词向量的空间分布
文章目录
-
-
-
- 1. 背景
- 2. 问题分析
-
- 为什么Bert词向量会呈现圆锥形的空间分布且高频词更靠近原点?
- 3. 理论解释
-
- 1)未出现词
- 2)低频词
- 论文1《[On the Sentence Embeddings from Pre-trained Language Models](https://arxiv.org/abs/2011.05864)》
- 论文2《[Learning to Remove: Towards Isotropic Pre-trained BERT Embedding](https://arxiv.org/abs/2104.05274)》
- 4. 总结
-
-
1. 背景
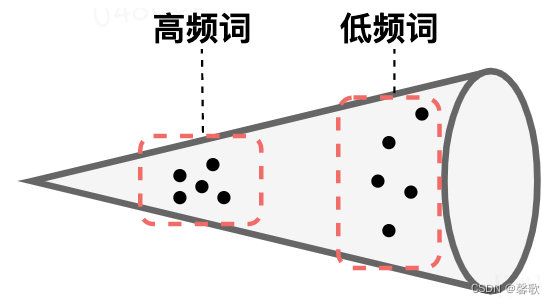
我们知道Bert 预训练模型针对分词、ner、文本分类等下游任务取得了很好的效果,但在语义相似度任务上,表现相较于 Word2Vec、Glove 等并没有明显的提升。有学者研究发现,这是因为 Bert 词向量存在各向异性(不同方向表现出的特征不一致),高频词分布在狭小的区域,靠近原点,低频词训练不充分,分布相对稀疏,远离原点,词向量整体的空间分布呈现锥形,如下图,导致计算的相似度存在问题。
2. 问题分析
为什么Bert词向量会呈现圆锥形的空间分布且高频词更靠近原点?

查了一些论文发现,除了这篇 ICLR 2019 的论文《Representation Degeneration Problem in Training Natural Language Generation Models》给出了一定的理论解释,几乎所有提及到 Bert 词向量空间分布存在问题的论文,都只是在引用该篇的基础上,直接将词向量压缩到二维平面上进行观测统计(肉眼看的说服力明显不够)
图中(b)(c)可以看出原生 Word2Vec 和分类任务的词向量经 SVD 投影,分布在原点周围,而原生 Transformer 则分布在圆锥形区域,且任意两个词向量都正相关,会降低模型性能,这种现象被称为表征退化问题。
- ①造成这种现象的直观解释是:在模型训练过程中,真词的embedding会被推向隐藏状态的方向,而其他词会被推向其负方向,结果是词汇表中大多数单词的嵌入将被推向与大多数隐藏状态负相关的相似方向,因此在嵌入空间的局部区域中聚集在一起。
- ②理论解释则是分析未出现词的嵌入,发现表征退化和隐藏状态的结构有关:当隐藏状态的凸包不包含原点时,退化出现,并且当使用层归一化进行训练时,很可能发生这种情况。并发现低频词很可能在优化过程中被训练为彼此接近,因此位于局部区域。
论文将对理论解释部分给出证明,下面从我的理解,来解读一下,最后再简单说一下另外两篇对 Bert 词向量观测统计的论文。
3. 理论解释
在介绍之前,先熟悉几个关于凸优化问题的概念(不知道其实也问题不大):
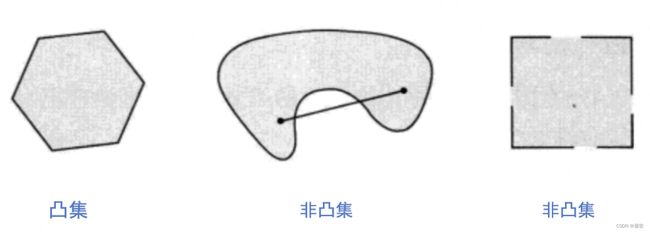
- 凸集:
集合 C 中任意两点的线段仍在 C 中,即对任意 x 1 , x 2 ∈ C , 0 ⩽ θ ⩽ 1 ,都有 θ x 1 + ( 1 − θ ) x 2 ∈ C 。 \quad\small 集合C中任意两点的线段仍在C中,即对任意x_1,x_2\in C,0\leqslant \theta\leqslant 1,都有\theta x_1+(1-\theta)x_2\in C。 集合C中任意两点的线段仍在C中,即对任意x1,x2∈C,0⩽θ⩽1,都有θx1+(1−θ)x2∈C。
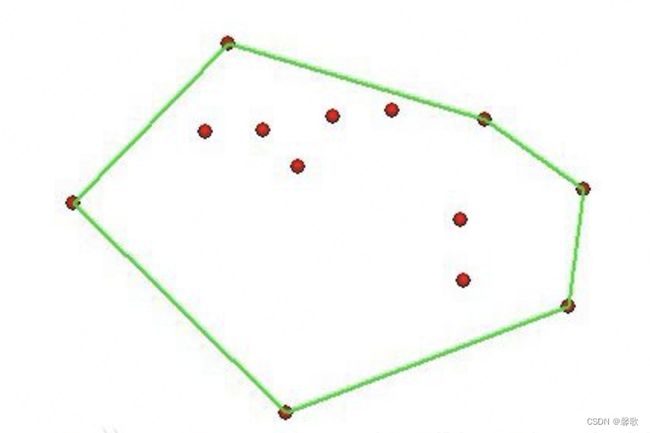
- 凸包:
点集Q的凸包是指一个最小凸多边形,满足Q中的点或者在多边形边上或者在其内。(最小的凸集)
- 锥:
对于集合 S 中的任意 x , λ ⩾ 0 ,满足 λ x ∈ S 。 \quad\small 对于集合S中的任意x,\lambda \geqslant 0,满足\lambda x \in S。 对于集合S中的任意x,λ⩾0,满足λx∈S。
- 凸锥:
如果一个集合既是锥,又是凸集,则该集合是凸锥。 ⇔ ∀ x 1 , x 2 ∈ C , θ 1 , θ 2 ⩾ 0 , 有 θ 1 x 1 + θ 2 x 2 ∈ C 。 \quad\Leftrightarrow \forall x_1,x_2 \in C,\theta_1,\theta_2 \geqslant 0,有\theta_1x_1+\theta_2x_2 \in C。 ⇔∀x1,x2∈C,θ1,θ2⩾0,有θ1x1+θ2x2∈C。
1)未出现词
因为不容易直接分析高、低频词,作者另辟蹊径,选择和低频词比较相似的未出现词来分析目标函数。
假定极端情况下 y i ≠ N , y i 表示词表中词的索引,即词嵌入 w N 的第 N 个词为不在语料库中,其他 参数固定并已优化好,则对应的词嵌入 w n 优化过程: \small 假定极端情况下y_i \neq N,y_i表示词表中词的索引,即词嵌入w_N的第N个词为不在语料库中,其他 \\参数固定并已优化好,则对应的词嵌入w_n优化过程: 假定极端情况下yi=N,yi表示词表中词的索引,即词嵌入wN的第N个词为不在语料库中,其他参数固定并已优化好,则对应的词嵌入wn优化过程:
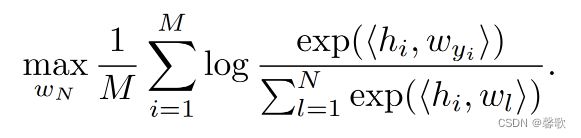
因为其他参数固定,则上式等价于:
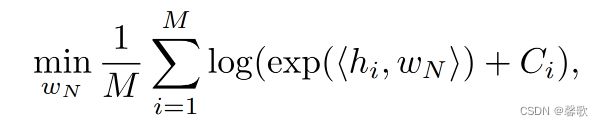
常量 C i = ∑ l = 1 N − 1 e x p ( < h i , w l > ) \scriptsize 常量\,C_i=\sum^{N-1}_{l=1}exp(
首先解释一下这一步的过渡,因为第 N 个词不在语料库中,所以该词与其他词没有任何联系, 在训练过程中优化 w N 时,不对其他词的 e m b e d d i n g 产生影响,即其他词的值都不变,对 w N 来 说是常数,未出现词应该获得最小的概率,所以优化目标为最小化未出现词的概率 \small \textcolor{red}{首先解释一下这一步的过渡,因为第N个词不在语料库中,所以该词与其他词没有任何联系,\\在训练过程中优化w_N时,不对其他词的embedding产生影响,即其他词的值都不变,对w_N来\\说是常数,未出现词应该获得最小的概率,所以优化目标为最小化未出现词的概率} 首先解释一下这一步的过渡,因为第N个词不在语料库中,所以该词与其他词没有任何联系,在训练过程中优化wN时,不对其他词的embedding产生影响,即其他词的值都不变,对wN来说是常数,未出现词应该获得最小的概率,所以优化目标为最小化未出现词的概率
定义1. 对于所有的隐藏状态,如果 < v , h i > < 0 ,则向量 v 是 h i 的一致负方向, i = 1 , . . . , M \small \textbf{定义1.}\quad对于所有的隐藏状态,如果
定理1. A . 如果一致负方向的集合非空,则它是凸的。 B . 如果 h i 存在一个一致负方向的向量 v , 则上式方程的最优解 ∣ ∣ w N ∗ ∣ ∣ = ∞ 并且可以通过设置 w N ∗ = l i m k → + ∞ k ⋅ v 实现。 \small \textbf{定理1.}\quad A.如果一致负方向的集合非空,则它是凸的。B. 如果h_i存在一个一致负方向的向量v,\\则上式方程的最优解||w_N^*||=\infty并且可以通过设置w_N^*=lim_{k\rightarrow +\infty}k\cdot v 实现。 定理1.A.如果一致负方向的集合非空,则它是凸的。B.如果hi存在一个一致负方向的向量v,则上式方程的最优解∣∣wN∗∣∣=∞并且可以通过设置wN∗=limk→+∞k⋅v实现。
文中说定理1 中的 A 显而易见,那就只能大家自行理解这个凸集了。B 则是对上面最小化公式的求解,下面给出证明。
证明:
定义 v 为一致负方向, k 为正数,则 l i m k → + ∞ ∑ i = 1 M l o g ( e x p ( < h i , k ⋅ v > ) + C i ) = ∑ i = 1 M l o g ( C i ) ,因为 ∑ i = 1 M l o g ( C i ) 是上式的下界且上式是凸的,所以 w ∗ = l i m k → + ∞ k ⋅ v 不仅是局部最优且是全局最优解。当且仅当 < h i , w N > 接近负无穷时,可以得到最优解 ∣ ∣ w N ∗ ∣ ∣ = ∞ 。 \small定义v为一致负方向,k为正数,则 lim_{k\rightarrow +\infty}\sum^M_{i=1}log(exp(
定理 1 是 w N 逼近无界的充分条件,由于一致负方向的集合是凸的,因此 w N 可能位于凸锥中, 并在优化过程中移动到无穷大。下面的定理 2 则是充分必要条件。 \small\textcolor{red}{定理1是w_N逼近无界的充分条件,由于一致负 方向的集合是凸的,因此w_N可能位于凸锥中,\\并在优化过程中移动到无穷大。下面的定理2则是充分必要条件。} 定理1是wN逼近无界的充分条件,由于一致负方向的集合是凸的,因此wN可能位于凸锥中,并在优化过程中移动到无穷大。下面的定理2则是充分必要条件。
定理2. 存在一个 v 是一组隐藏状态的一致负方向,当且仅当隐藏状态的凸包不包含原点。 \small \textbf{定理2.}\quad 存在一个v是一组隐藏状态的一致负方向,当且仅当隐藏状态的凸包不包含原点。 定理2.存在一个v是一组隐藏状态的一致负方向,当且仅当隐藏状态的凸包不包含原点。
证明:
必要性 ( 反证法 ) : 假设有 M 个隐藏状态,如果隐藏状态 h i 的凸包包含原点且存在一致负方向 v ,从凸包的定义 可知存在 α i ,可得 ∑ i M α i h i = 0 , α i ⩾ 0 且 ∑ i α i = 1 ,两边同时乘以 v ,则 ∑ i α i < h i , v > = 0 ,与 < h i , v > < 0 相矛盾。 \small 必要性(反证法):\\假设有M个隐藏状态,如果隐藏状态h_i的凸包包含原点且存在一致负方向v,从凸包的定义 \\ 可知存在\alpha_i,可得\sum^M_i\alpha_ih_i=0,\alpha_i\geqslant 0且\sum_i\alpha_i=1,两边同时乘以v,则\sum_i\alpha_i
充分性: 如果隐藏状态的凸包 h i 不包含原点,则至少存在一个通过原点但与凸包不相交的超平面 H , 则容易得出 H 半空间的法线是一致负方向。 \small 充分性:\\如果隐藏状态的凸包h_i不包含原点,则至少存在一个通过原点但与凸包不相交的超平面H,\\ 则容易得出H半空间的法线是一致负方向。 充分性:如果隐藏状态的凸包hi不包含原点,则至少存在一个通过原点但与凸包不相交的超平面H,则容易得出H半空间的法线是一致负方向。
以上还是很好理解的,定理1说明未出现词的向量会被优化无穷远,远离原点(模越来越大)。定理2则是说明词向量的分布不包含原点,而是在原点的一侧
2)低频词
低频词的分析则是在未出现词的基础上,因为分析低频词的embedding对损失函数的影响,将损失函数分为了两部分:
(1) A w N 为不包含 w N 的其他句子,在该集合中, w N 被视为未出现的 t o k e n 。 H A w N 为 A w N 的隐藏状态空间, P A w N 为 H A w N 的概率分布,且二者连续,则: \small\textbf{(1)}A_{w_N}为不包含w_N的其他句子,在该集合中,w_N被视为未出现的token。H_{A_{w_N}}为\\ A_{w_N}的隐藏状态空间,P_{A_{w_N}}为H_{A_{w_N}}的概率分布,且二者连续,则: (1)AwN为不包含wN的其他句子,在该集合中,wN被视为未出现的token。HAwN为AwN的隐藏状态空间,PAwN为HAwN的概率分布,且二者连续,则:
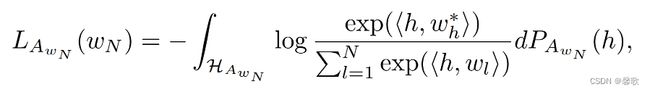
这是最大化对数似然的广义版本。
(2) B w N 为包含 w N 的句子集, w N 会出现在 B w N 中的每个句子,在一些情况下,需 要基于 w N 计算隐藏状态,例如用 w N 的隐藏状态去预测 w N 后面的词,另一方面, 用隐藏状态去预测 w N , B w N 的损失函数为: \textbf{(2)}B_{w_N}为包含w_N的句子集,w_N会出现在B_{w_N}中的每个句子,在一些情况下,需\\要基于w_N计算隐藏状态,例如用w_N的隐藏状态去预测w_N后面的词,另一方面,\\用隐藏状态去预测w_N,B_{w_N}的损失函数为: (2)BwN为包含wN的句子集,wN会出现在BwN中的每个句子,在一些情况下,需要基于wN计算隐藏状态,例如用wN的隐藏状态去预测wN后面的词,另一方面,用隐藏状态去预测wN,BwN的损失函数为:
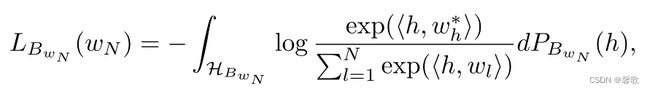
总损失函数为:
![]()
A w N 的损失是凸的,而 B w N 的损失比较复杂,通常相对于 w N 是非凸的。一般思路 是假定 L A w N ( w N ) 具有良好理论特性的凸函数,如果 P ( s e n t e n c e s i n A w N ) 足够大,接近 1 − ϵ , 并且 L B w N ( w N ) 是有界光滑函数,则 L ( w N ) 的最优解接近 L A w N ( w N ) 的最优解, 且 L A w N ( w N ) 强凸时,解唯一。正规表述如定理 3 : A_{w_N}的损失是凸的,而B_{w_N}的损失比较复杂,通常相对于w_N是非凸的。一般思路\\是假定L_{A_{w_N}}(w_N)具有良好理论特性的凸函数,如果P(sentence\,s\,in\,A_{w_N})足够大,接近1-\epsilon,并且L_{B_{w_N}}(w_N)是有界光滑函数,则L(w_N)的最优解接近L_{A_{w_N}}(w_N)的最优解,\\ 且L_{A_{w_N}}(w_N)强凸时,解唯一。正规表述如定理3: AwN的损失是凸的,而BwN的损失比较复杂,通常相对于wN是非凸的。一般思路是假定LAwN(wN)具有良好理论特性的凸函数,如果P(sentencesinAwN)足够大,接近1−ϵ,并且LBwN(wN)是有界光滑函数,则L(wN)的最优解接近LAwN(wN)的最优解,且LAwN(wN)强凸时,解唯一。正规表述如定理3:
定理3. 给定一个 α 强凸的函数 f ( x ) 和一个满足黑塞矩阵 H ( g ( x ) ) ≻ − β I 的 g ( x ) , I 为单位矩阵,且 ∣ g ( x ) ∣ < B 。给定一个 ϵ > 0 , x ∗ 和 x ϵ ∗ 分别为 f ( x ) 和 ( 1 − ϵ ) f ( x ) + ϵ g ( x ) 的最优解,若 ϵ < α α + β ,则 ∣ ∣ x ∗ − x ϵ ∗ ∣ ∣ 2 2 ≤ 4 ϵ B α − ϵ ( α + β ) 。 \small\textbf{定理3.}\quad 给定一个\alpha强凸的函数f(x)和一个满足黑塞矩阵\textbf{H}(g(x))\succ -\beta \textbf{I}的g(x),\textbf{I}为单位矩阵,且|g(x)| < B。给定一个\epsilon > 0,x^*和x^*_\epsilon 分别为f(x)和(1-\epsilon)f(x)+\epsilon g(x)的最优解,若\epsilon < \frac{\alpha}{\alpha+\beta},则||x^*-x^*_\epsilon||^2_2\le \frac{4\epsilon B}{\alpha-\epsilon(\alpha+\beta)}。 定理3.给定一个α强凸的函数f(x)和一个满足黑塞矩阵H(g(x))≻−βI的g(x),I为单位矩阵,且∣g(x)∣<B。给定一个ϵ>0,x∗和xϵ∗分别为f(x)和(1−ϵ)f(x)+ϵg(x)的最优解,若ϵ<α+βα,则∣∣x∗−xϵ∗∣∣22≤α−ϵ(α+β)4ϵB。
原来定理3 才是理解路上的最大绊脚石!
文中有给出证明(下面会贴出) , 我的理解是对于 A 、 B 两个集合,当句子 S 在 A 中的概率 ( 1 − ϵ ) 越大时,总损失函数越接近 f ( x ) ,总损失函数的最优解 x ϵ ∗ 与未出现词损失函数的最优解 x ∗ 的 l 2 距离即 ∣ ∣ x ∗ − x ϵ ∗ ∣ ∣ 2 2 越小,反之,趋向 g ( x ) , ∣ ∣ x ∗ − x ϵ ∗ ∣ ∣ 2 2 越大。( 4 ϵ B α − ϵ ( α + β ) 是 ϵ 的增函数) 文中没有给出高频词的分析,因为当 ϵ 越大时,这个词越是高频词。 \small \textcolor{red}{文中有给出证明(下面会贴出),我的理解是对于A、B两个集合,当句子S在A中的概率(1-\epsilon)越大时,总损失函数越接近f(x),总损失函数的最优解x^*_\epsilon 与未出现词损失函数的最优解x^*的\\ l2距离即||x^*-x^*_\epsilon||^2_2越小,反之,趋向g(x),||x^*-x^*_\epsilon||^2_2越大。(\frac{4\epsilon B}{\alpha-\epsilon(\alpha+\beta)}是\epsilon的增函数)\\文中没有给出高频词的分析,因为当\epsilon越大时,这个词越是高频词。} 文中有给出证明(下面会贴出),我的理解是对于A、B两个集合,当句子S在A中的概率(1−ϵ)越大时,总损失函数越接近f(x),总损失函数的最优解xϵ∗与未出现词损失函数的最优解x∗的l2距离即∣∣x∗−xϵ∗∣∣22越小,反之,趋向g(x),∣∣x∗−xϵ∗∣∣22越大。(α−ϵ(α+β)4ϵB是ϵ的增函数)文中没有给出高频词的分析,因为当ϵ越大时,这个词越是高频词。
下面简述一下对词向量进行观测统计的论文
论文1《On the Sentence Embeddings from Pre-trained Language Models》
其实这篇论文就是字节的 Bert-flow(不熟悉 Bert-flow 可见《对比学习——文本匹配》)。论文计算了词嵌入与原点的平均l2距离,并根据词频做了排序(词频越高排名越靠前,第0位词频最高),得出高频词靠近原点、低频词远离原点的结论,如下表上半部分:
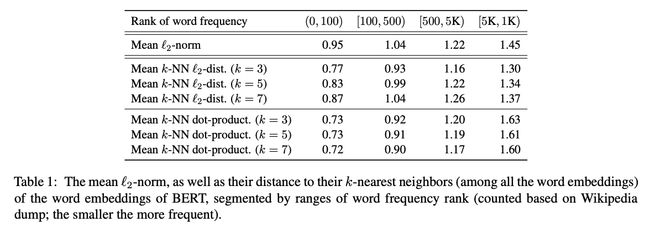
表的下半部分则为词嵌入和它的k个近邻之间的平均l2距离和点积,可以看出低频词相较于高频词,和它们的k近邻距离更远,说明低频词相对高频词分布更稀疏。
论文2《Learning to Remove: Towards Isotropic Pre-trained BERT Embedding》
该论文则是通过随机计算两个词的相似度,发现都远大于0(说明词向量的方向基本都一致,不一致不会都远大于0),以此说明词向量不是均匀分布在向量空间中,而是分布在一个狭窄的圆锥体中。
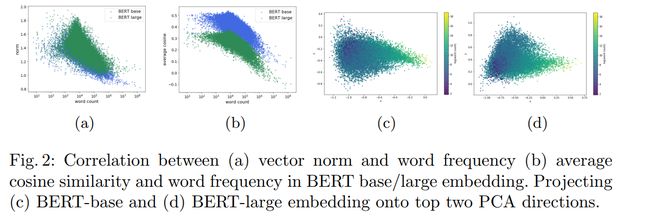
4. 总结
都有理论解释了,结论自然就是 Bert 词向量确实存在表征退化问题,词向量存在各向异性,高频词距离原点更近,低频词训练不充分,远离原点,整体分布呈现圆锥形,导致其不适用于语义相似度任务。不过不知道该理论解释有没有说服你。针对此类问题,可以采用一下方法对其进行纠正,如论文[1]中加入cos正则,论文[2]中将锥形分布转化为高斯分布,《对比学习——文本匹配》其实都是为了解决这个问题,因为词向量有问题,句向量自然跑不了。
附:(定理3证明)