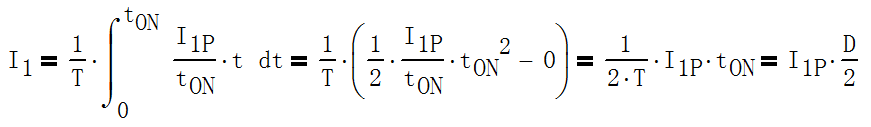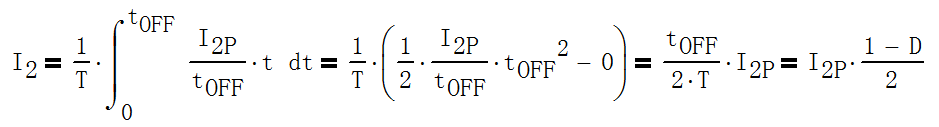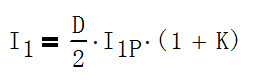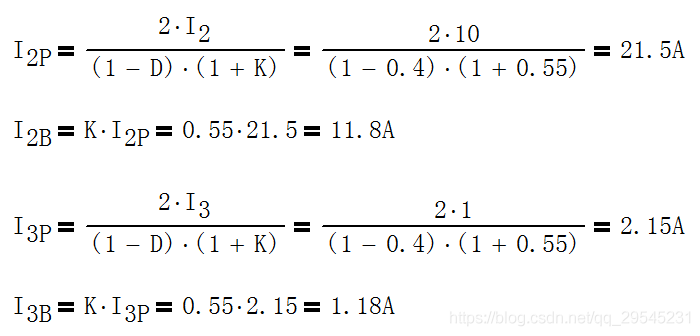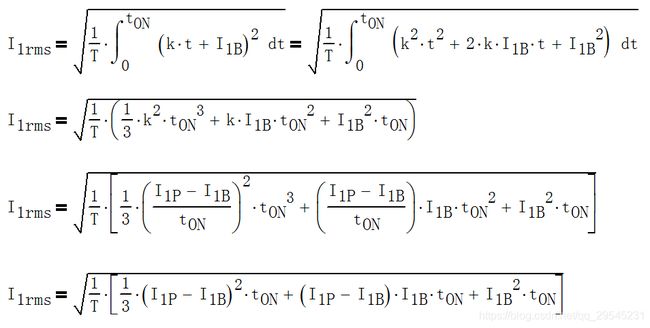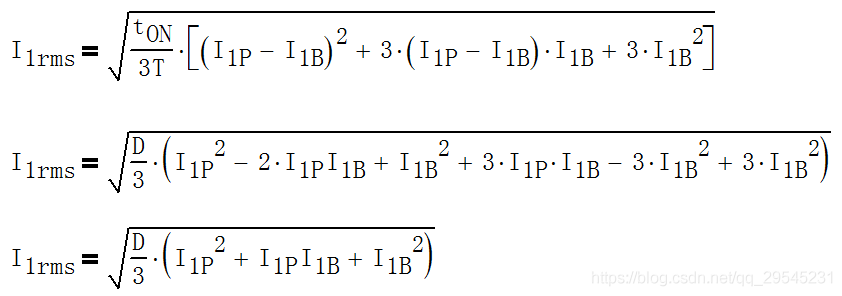三角波电流与梯形波电流的分析
- 三角波电流的峰值与平均值之间的关系
电流平均值的计算方法是先在一个周期T内积分,再除以T,单位为A。下图为自激式开关电源一、
二次绕组周期性三角波电流示意图。其一次绕组电流的峰值I1P和平均值I1之间的关系,推导如下:
设电流的时间函数为I1(t)=kt,其中,k=I1P/tON,则有
t = 0时,I1(0) = 0;
t = tON时,I1(tON) = I1P
于是,I1(t) = kt可以表示为I1(t) = I1P*t/tON。因此,峰值为I1P的三角波电流平均值I1为
式中,D = tON / T。
一次绕组的电流峰值I1P和平均值I1之间的关系可以这样理解:电流的峰值I1P与tON包围的三角形“等积变形”
整个周期T的矩形,则矩形的纵向高就是平均值I1。直观的如上图所示。黑色大三角的面积等于黑色小三角与黑色
矩形面积之和,灰色梯形是公共面积。
二次绕组的电流峰值I2P和平均值I2之间也有类似的关系,但二次绕组电流过程时间为tOFF , 故需要把公式中的D
换成1-D,即
- 三角波电流的峰值与有效值之间的关系
有效值也称均方根值或称方均根值,它的计算方法是先平方,然后在一个周期T内积分、除以T、开方,
符号为rms。比如,幅度为100V而占空比为0.5的方波信号,如果按平均值计算,它的电压只有50V,
而按方均根值计算则有50√2V。
这是为什么呢?举一个例子:有一组100V的电池组,每次供电10min之后停10min,也就是说占空比为一半。
如果这组电池带动的是10欧电阻,供电的10min产生10A的电流和1000W的功率,停电时电流和功率为零,
那么在20min一个周期内的平均功率为500W,这相当于50√2V的直流电向10欧电阻供电所产生的功率
(W = U2/R = (50√2)2/10 = 500W),而50V直流电压向10欧电阻供电只能产生250W(502/10=250)的功率。
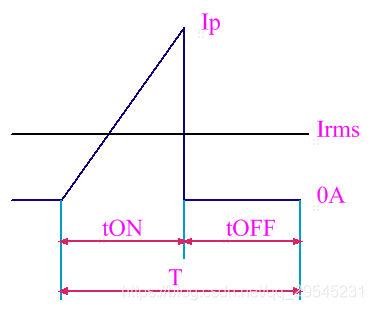
下图为自激式开关电源一次绕组周期性三角波电流示意图。其电流的峰值I1P与有效值I1rms之间的关系推导如下:
设三角波电流的时间函数为I1(t) = I1P*t/tON , 因此,峰值为I1P的三角波电流有效值I1rms为
式中,D = tON /T。
二次绕组电流的峰值I2P和有效值I2rms之间也有类似的关系,但二次绕组电流过程时间为tOFF ,
故需要把公式中的D换成1-D,即
- 梯形波电流的峰值与平均值的关系
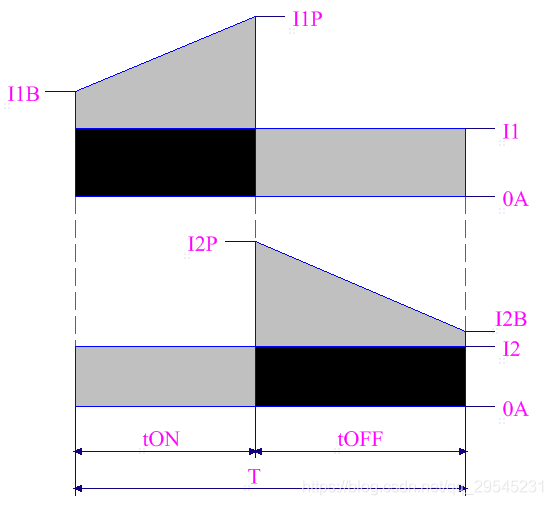
下图为反激式开关电源CCM模式一、二次绕组梯形波电流示意图,其一次绕组电流峰值I1P、
最小值I1B与平均值I1、有效值I1rms之间有其内在数量关系。
设电流的时间函数为 I1(t) = kt + b 式中,k = (I1P-I1B)/tON ,那么有
t = 0时,I1(0) = I1B;
t = tON时,I1(tON) = I1P
于是I1(t) = kt + b 可以表示为
因此,梯形波电流平均值I1为
式中,D = tON/T。
若把I1B=K*I1P代入上式,得
二次绕组电流峰值I2P、最小值I2B和平均值I2之间也有类似的关系,但二次绕组电流过程时间为tOFF,
故需要把公式中的D换成1-D,即
其一次绕组电流峰值I1P、最小值I1B与平均值I1之间的关系可以这样理解:电流峰值I1P、最小值I1B与
tON包围的梯形“等积变形”整个周期T的矩形,则矩形的纵向高就是电流平均值I1。如上图的灰色梯
形面积等于灰色矩形,黑色矩形是公共面积。
举例说明 ( 已知K=0.55, 二次绕组1的平均电流I2 = 10A,二次绕组2的平均电流I3 = 1A, 占空比D = 0.4 ,
计算峰值电流和最小值电流 )
- 梯形波电流的峰值与有效值
电流的时间函数I1(t) = kt + b,因此I1的有效值I1rms为
式中,D =tON/T。
若把I1B = K*I1P代入上式,得
二次绕组电流峰值I2P、最小值I2B和有效值I2rms之间也有类似的关系,但二次绕组电流过程时间为tOFF,
故需要把公式中的D换成1-D,即