GAMES202-Shadow总结概括
截图均来自于闫令琪老师的GMAES202-Shadow,本文在于对课程内容进行总结以及加上自己的理解,希望帮助同学们加深对课程内容的理解,如有谬误请各位指正
复习本节需要的基本知识
1. Shadow Mapping
为了获得一张Shadow Mapping,需要我们对场景进行两次渲染
第一次渲染时,将摄像机放置于光源处,用depth test获得一幅带有深度值的纹理
第二次渲染时,将摄像机放置原处,再次记录看到的点到光源的距离
将第二次得到的值与第一次得到的深度值进行比较,如果大于第一次的深度值则说明该点在阴影中,如果等于则说明不在阴影中

2. Mipmap
多级渐远纹理(Mipmap)本质上是根据距离选择不同的纹理(但不是LOD)
Mipmap原理类似于基于距离的线性纹理过滤(Opengl中分为线性过滤与邻近过滤)
线性过滤可以理解为对周围像素进行加权插值,得到的是一个平均颜色
邻近过滤可以理解为选择最近的一个像素颜色
Mipmap可以避免远距离采样频率低和数据频率高造成的摩尔纹或者失真,同时具有良好的性能。
本节内容
1. 自遮挡现象
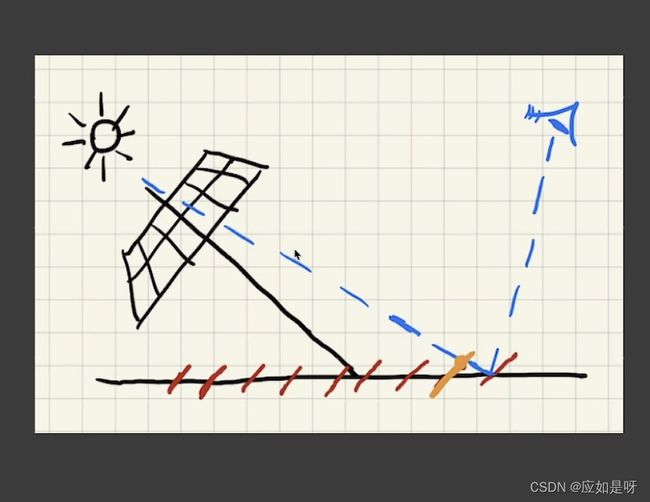
Shadow map上面记录的是一格一格像素的不连续的深度值,而如上图中,shadow map连出的蓝色的线本应该记录红色部分的深度值,而被黄色部分遮挡住了,造成了显示的错误
如果光源从头顶向下直射则不会造成自遮挡现象
如果光源从左边或者右边射入则会造成更为严重的的自遮挡现象
那么如何解决这个问题呢?

可以增加一段偏移值,即图上黄色的部分,在偏移值内部的遮挡可以忽略不计,这个bias不是一个固定值,可以根据光源到地面的角度来进行改变,例如如果光源从上往下直射地面,这时自遮挡现象不明显,则可以减小bias的值
但是同时偏移值的加入也带来了阴影丢失的问题(有时候bias太大反而会把正确的阴影去除掉)
在工业界通过调整最合适的bias值可以大致解决此问题
在学术界通过Second-depth shadow mapping方法
即记录最小深度于与第二小深度再对两者进行平均,使用中间的深度做阴影比较
2.PCF(Percentage Closer Filtering)
在绘制ShadowMapping时我们会遇到明显的硬阴影(图上)
而在现实生活中我们更常见到的是软阴影(图下)

为了让显示效果更加符合实际 我们则需要PCF对阴影进行过滤(在阴影判断阶段)
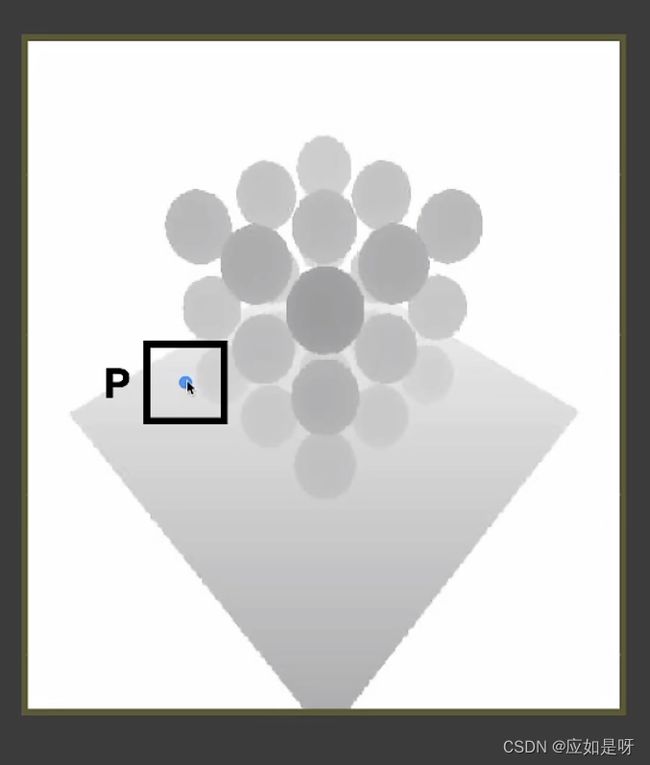
上图为一张ShadowMapping,我们选取p点为例,对p点周围的像素进行采样,例如为3✖️3的每一格的深度值都与shading point进行比较(即判断是否被遮挡),得出一组为3✖️3的值为0或1的表(比较得出的结果非0即1),然后对这些01值进行加权平均(即滤波操作),最终得到一个visibility的值(大于0小于1)
3. PCSS(Percentage Closer Soft Shadows)
在现实生活中我们常碰到一种现象:在树的到树根部分的阴影更深,而在树叶部分的阴影更浅,为了实现这种效果,我们使用了PCSS方法,即根据遮挡物的距离来对阴影的软硬程度进行调节

w P e n u m b r a = ( d R e c e i v e r − d B l o c k e r ) ⋅ w L i g h t / d B l o c k e r w_{Penumbra}=(d_{Receiver}-d_{Blocker} )\cdot w_{Light}/d_{Blocker} wPenumbra=(dReceiver−dBlocker)⋅wLight/dBlocker
上述公式是 由上图两个黄色三角形相似推导得出
w用来表示阴影的软硬程度
而为了得到w的值,必须要知道blocker的depth,将每一个点得到的depth进行均值操作得到的average blocker depth即是我们要的深度值。
PCSS的全部操作可以概括为:
- 计算平均blocker深度
- 计算w值
- 使用PCF
缺点:
- 第一步和第三步比较慢(因为需要大量的采样,阴影越软,采样范围越大)
- 采样则会产生噪声,造成得到的visivility图上会有很多噪声
4. VSSM(Variance Soft Shadow Mapping)
VSSM则是对第一步和第三步采样慢的一个解决思路
第三步PCF的本质是加权平均比较得出的01值,即可近似看作,有百分之多少的texel的深度比shading point的深度浅
于是我们可以把采样的问题转化成从直方图或正态分布上找大概所占的百分比

那么如何得到正态分布呢?
在概率论中我们可以通过期望和方差来得到某个模型的正态分布
期望(即均值)我们可以通过MipMap来得到,但MipMap只能得到正方形的
为了得到矩形的均值我们使用SAT(Summed Area Tables)方法
方差我们可以通过下面这个公式, 即方差=平方的期望-期望的平方
V a r ( X ) = E ( X 2 ) − E 2 ( X ) Var(X)=E(X^2)-E^2(X) Var(X)=E(X2)−E2(X)
我们则需要两张Shadow Map一张记录深度一张记录深度的平方
(tips:在OpenGL中将两张深度值写入RGB的两个通道即可,不需要一个额外的纹理)
通过得到的方差和均值我们可以计算正态分布,接着只需要知道阴影部分的面积即可得到百分比,计算面积时可以使用误差函数对正态分布的数值解进行打表并储存,当需要使用的时候调用即可

但大佬们发现了更加简便的方法——通过切比雪夫不等式来解决这个问题
P ( x > t ) ⩽ σ 2 σ 2 + ( t − μ ) 2 P(x>t)\leqslant\frac{\sigma^2}{\sigma^2+(t-\mu)^2} P(x>t)⩽σ2+(t−μ)2σ2
μ \mu μ为期望 σ 2 \sigma^2 σ2为方差
如图为通过切比雪夫不等式计算得到的面积(红色阴影),即我们所需要的百分比值
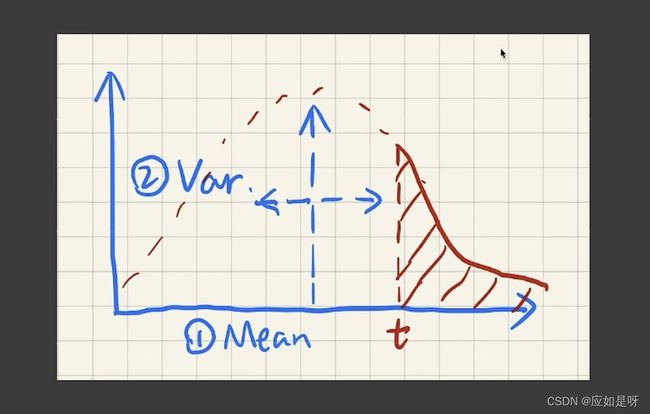
在实时渲染中为了得出近似的效果可以直接把不等式作为值的估计
(切比雪夫不等式有一个限制是t必须在 μ \mu μ的左面,否则会造成估计不准确)
刚刚说到第一步和第三步的采样都对系统性能有影响,现在我们解决了第三步的采样问题,那如何解决第一步呢
第一步是为了计算遮挡物的平均深度
如下图
假设shading point对应的深度为7
蓝色的值<7,则蓝色为遮挡物的深度

我们定义
Blocker (z
Unblocker (z>t), avg. z u n o c c z_{unocc} zunocc
z a v g z_{avg} zavg则是对这些数加起来的平均
则有
N 1 N z u n o c c + N 2 N z o c c = z a v g \frac{N_1}{N}z_{unocc}+\frac{N_2}{N}z_{occ}=z_{avg} NN1zunocc+NN2zocc=zavg
我们可以利用上面提到的切比雪夫不等式
N1/N = P(x>t)
N2/N=1-P(x>t)
同时近似非遮挡物的深度等于shading point的深度,即 z u n o c c = t z_{unocc}=t zunocc=t
这时除了 z o c c z_{occ} zocc遮挡物深度我们所有的值都已经计算出来了,结果显而易见解一个一元一次等式即可得到
如此一来PCSS第一步和第三步的采样问题通过VSSM转换成了性能消耗更低的做法
5. SAT for Range Query
上面说到通过SAT方法来计算均值
而计算均值本质上就是范围内求和然后除以元素个数
我们则可以引用前缀和这一概念
即红色数据的值为当前位置之前每一项蓝色的和
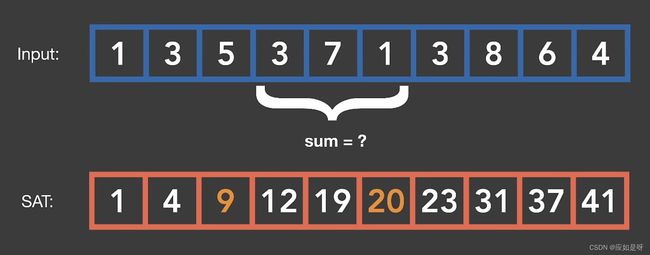
那么要计算某一段的和例如图中的sum则可以通过前六个数的和20减去前三个数的和9得到
在二维情况下
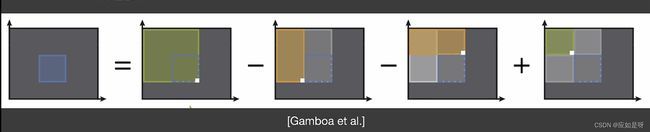
要得到蓝色格子内的值则需要用绿色格子减去横竖两个黄色格子的值,因为重复剪掉了左上角的值则需要再加上左上角绿色格子的值
我们可以建立一张表,每一行从左上角加到某个元素的值,再对每一列做相同操作
复杂度为O(m x n)
同时每一行都是并行计算的,则可以通过GPU比较快的完成表的建立
6. Moment Shadow Mapping
VSSM尽管十分巧妙,但也存在一些问题
如下图正态分布可能造成阴影漏光的问题

为了让分布更加准确我们可以使用更高阶的矩来描述分布
即类似于泰勒展开于傅立叶展开,记录多少次方就是保留前多少阶的矩
下图展示了不同阶矩对分布的影响

通过使用四阶的矩我们就近似的解决了分布不准确,即阴影漏光的问题