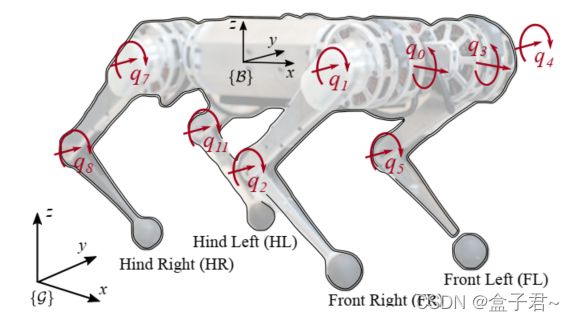
【论文解读--MPC+WBC控制】（Cheetah mini）Whole-Body Impulse Control and Model Predictive Control

系列文章目录

提示：这里可以添加系列文章的所有文章的目录，目录需要自己手动添加
TODO:写完再整理

---

前言

认知有限，望大家多多包涵，有什么问题也希望能够与大家多交流，共同成长！

本文先对高动态四足机器人全身脉冲控制WBC与模型预测控制MPC做个简单的介绍，具体内容后续再更，其他模块可以参考去我其他文章

---

提示：以下是本篇文章正文内容

一、简介

本文提出了一种将全身力控制（WBC）和模型预测控制（MPC）相结合的控制器

模型预测控制MPC找到了一个最佳的反作用力分布一个简单的模型【MPC可以看成一个优化器，输出的是预测控制量】

全身力控WBC根据MPC计算的反作用力，计算关节扭矩、位置和速度命令【WBC是一个控制器】

WBIC主要是用于跟踪地面反作用力剖面，而不是躯干的轨迹
MPC和WBC都有各自的模型，其中MPC使用的是单刚体集中质量块模型，WBC使用的是多体模型【防盗标记–盒子君hzj】

本文主要贡献：
1）发明一种通用的鲁棒控制四足机器人高动态运动方案
2）展示高速奔跑和各种步态在真正的硬件上，在迷你猎豹机器人上。

.
.

二、控制架构

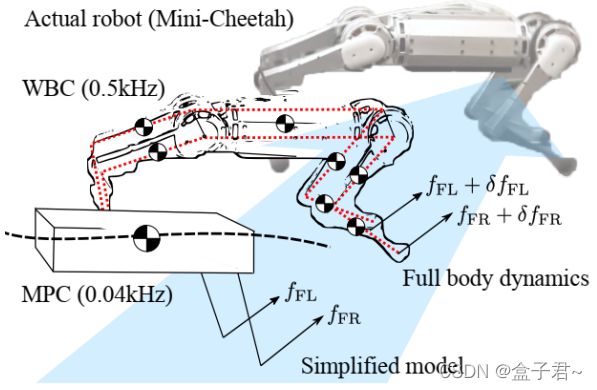
控制架构包括包括两部分：模型预测控制和全身控制。反作用力由MPC计算，WBC根据反作用力实现支撑腿和摆动腿同时控制，WBC中的最终命令被发送到机器人执行动态移动

1、控制流程

MPC使用RC控制器中用户命令的步态类型、速度和方向，【防盗标记–盒子君hzj】计算所需的步态反作用力和脚/身体位置指令。根据这些，WBC计算传递给每个关节水平控制器

2、摆动腿落点规划器

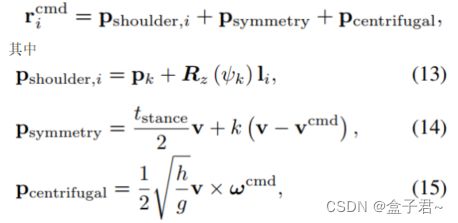
pk是第k个时间步处的身体位置，并且li是第i腿肩部相对于身体局部的位置框架。因此，pshoulder；i是第i个肩部位置尊重全局框架。对称性就是所谓的Raibert启发式[20]强制腿的着地角度并离开如果机器人按指令行驶，则角度相同速度。在我们的设置中，我们使用0.03作为反馈增益k

.

3、状态估计器（用于估计躯干的位置、速度、姿态）

我们使用基于卡尔曼滤波器的状态估计器来计算基于运动学数据**（与猎豹三的方式相近）**
尽管状态估计器和动力学引擎的对于四足机器人表演贡献很大，我们不作解释因为它们不在本文的讨论范围之内。
.

4、步态调度器和步态规划器

一个接触序列是由步态调度器和步态规划器预定义

大多数步态基本上是周期性的，使用了一种基于周期性相位的步态调度器，只需要两个参数来指定步态类型即是每只脚的相位偏移和站姿周期。适当的摆动间隔一个周期的站姿周期足以定义步态。【防盗标记–盒子君hzj】我们可以通过改变步态频率循环持续时间。因为步态是由一部分定义的在周期的站姿/摆动周期中，步态类型为即使步态频率改变也能保持

.
.

三、模型预测控制MPC

我们MPC的目标是找出使集中质量遵循给定的轨迹的反作用力

1.MPC使用的集中质量动力学模型（用于预测泛作用力f）

其中，一个是平移动力学模型，一个是角动量模型
p表示机器人位置
fi表示机器人反作用力
cg表示机器人重力
m是机器人的身体质量
nc是接触的数量
I是转动惯量张量
w是躯干的角速度
ri是第i个接触点相对于到机器人的CoM，相当于接触力的臂
.

2.模型简化假设

（1）模型第一个简化–滚转角和俯仰角都很小（roll=pitch=0）进而简化坐标转换

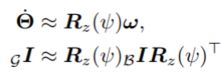
（这个与猎豹3 的简化思想是一致的）

（2）模型第二个简化–机器人状态接近命令的轨迹

（3）模型第三个简化–惯性张量的对角线外条件也很小【防盗标记–盒子君hzj】

基于上面的假设，我们把质量集中模型近似表达为

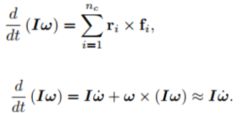
（4）（经过线性化和简化后的）质量集中模型再经过离散化得到系统的离散动力学方程

其中：

MPC的计算方法是和猎豹 3的方法步骤一致的，这里不再说明了，请转战一下我其他的博客
https://blog.csdn.net/qq_35635374/article/details/121952459

.
.

四、WBC全身脉冲控制

利用MPC发现的反作用力，WBIC计算关节位置、速度和扭矩命令。

WBIC计算期望的关节位置和速度。利用关节位置反馈有利于动态由于其控制输入并置，【防盗标记–盒子君hzj】所以可以进行运动控制以及高频更新

WBC 的英文全称为 Whole Body Control。为了降低运动控制算法的复杂性，控制任务通常会被分解为一组较为简单的任务，如保持平衡的躯干姿态控制，摆动相的足底轨迹跟随，或者用于防止滑动的接触力约束。每一个任务往往都需要多个驱动关节配合完成，同时每一个驱动关节又同时服务于多个任务，适应这种任务分解的理论框架是全身控制（WBC）。一般来说，为实现一组任务，所有驱动关节都能得到控制信号的控制系统都可以称作全身控制

.
.

1.WBC使用的多体动力学模型（计算每个关节的力矩）

多体动力学模型比集中质量模型更精确，使用WBIC来实现利用全身动力学控制带宽高频反馈控制

多体动力学模型描述如下

其中A、b、g、τ、fr和Jc分别是广义质量矩阵，科里奥利力，重力，关节力矩，反作用力和接触雅可比。
.

2.优先任务执行（为了计算关节位置、速度和加速度）

为了计算关节位置、速度和加速度，我们利用严格控制任务的反向运动学算法优先。

1、逆运动学公式是通过逆雅J可比矩阵得到的
2、计算期望的关节位置、速度：

为了执行优先任务，我们使用了空空间投影技术，这使得计算效率高的方法。当q=q>fq>j>是一个表示完整配置空间的向量，迭代
规则如下：

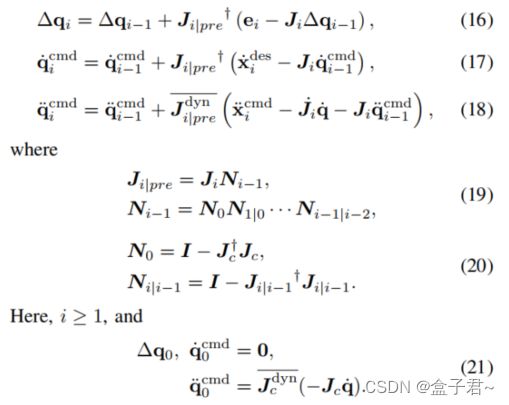
EI是由XDEI I和XI定义的位置误差，X是CMD I。第i个任务的加速命令由定义：

其中Kp和Kd是位置和速度反馈增益，分别是。注意等式（16）中没有反馈增益，这可以解释为使用统一收益。Jijpre是第i个任务雅可比矩阵在零空间的投影先前的任务。

Jc是一个接触Jacobian，它等价于下面方程式中的Jc

式（16）和（17）用于找到所需的接合位置和分别为联合PD控制器的速度。我们计算通过添加式（16）至测量接头位置计算出的联合命令q cmd j和q_ucmd j被发送到联合级PD控制器和加速指令q¨cmd被传送到QP优化以找到扭矩命令。【防盗标记–盒子君hzj】

.
.

3.二次规划（为了计算关节转矩指令）

为了计算转矩指令，我们使用二次优化QP以找到反作用力，减少加速度指令跟踪误差与反作用力。满足不等式约束的指令跟踪合成的反作用力。

我们用加速度计算最后的反作用力在上一步中找到的命令和反作用力在MPC中获得。对于优化，我们使用对小问题有效的开源QP解算器
QP问题的公式是

其中
δf和δfr 是浮动基加速度和反应力的松弛变量。
frMPC 和 Sf是MPC 和浮动基选择矩阵分别计算的反应力

.

4.计算最终扭矩命令

加速度q¨两个项插入式代入多体模型中

右边的所有条件都是已知的，我们可以很容易求解并获得联合扭矩指令τj

.
.

五、效果（各种步态的演示）

---

总结

控制器在六种不同的步态上进行测试环境，包括户外和跑步机上最高速度3:7 m=s。s【防盗标记–盒子君hzj】

集成WBC和MPC使我们的控制器通用而且强壮，在我们的控制器中执行或添加更多任务（例如，选择不同的步态可以通过改变我们公式中的足迹模式和时间，以及诸如摆动脚控制、躯干平衡控制是自动的由我们的控制方案自动完成）无需在飞行或欠驱动期间进行人工规划

以模型预测控制为核心，使用 MPC 求得足底反力；使用 WBC 计算关节空间的期望位置、期望速度与加速度；最后，通过多刚体动力学求得各个关节扭矩；同时也借鉴了 VMC算法与 SLIP 模型的部分理念，最终实现了四足机器人在非结构化路面上全方位稳定行走，并能在一定的侧向冲击扰动下恢复稳定