数字三角形【第十一届】【省赛】【C组】Python 【dfs 超时50分 、记忆化递归 dp+备忘录、dp+奇偶找规律 】

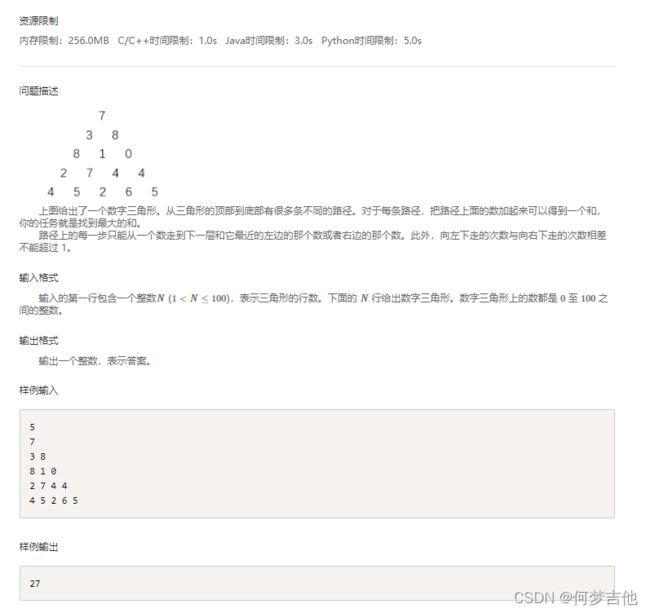
题目

分析

方法一：dfs（考试dp一般都很难想，暴搜尽量多拿分！！！）
乍一看是一个搜路径和最大值的问题，用dfs搜出每一条路径，从上至下，计算每一条的和，最后取哪一条？看题目

想左走和向右走次数不超过1

不要局限于字面意思，只考虑最终情况之差<=1
为dfs函数传入两个left right 记录当前经历过左下↙和右下↘而来，最后只选择满足的 最大值

注意边界条件
i=0 i=j

#TLE 50分
n=int(input())
a=[]
for i in range(n):
    a.append(list(map(int,input().split())))

def check(row,col):
    if row>=n:
        return False
    if col>row:
        return False
    return True

maxx=-1
def dfs(row,col,l,r,cnt):
    global a,n,maxx
    if row == n-1 and abs(l-r)<=1:#遍历所有可能，找到符合条件的 最大的那一个
        maxx=max(maxx,cnt)
        return 
        
    for d in {(1,0),(1,1)}:
        nrow,ncol = row+d[0],col+d[1]
        if check(nrow,ncol):
            if d==(1,0):
                dfs(nrow,ncol,l+1,r,cnt+a[nrow][ncol])#第一次写这里错了，该层值初始化为该层节点值
            else:
                dfs(nrow,ncol,l,r+1,cnt+a[nrow][ncol])
dfs(0,0,0,0,a[0][0])
print(maxx)

规模n=100，要搜的规模很大，能否剪枝！？(TAT 我还没学过剪枝！！！改变思路能否用dp？)
**方法二：记忆化递归=》dp+备忘录 **
如果用记忆化递归，需要从底向上搜，最终搜到i=1

1)当数字三角形有奇数行时，我们需要走偶数步，所以左移步数和右移步数一定相同，最后一定会到达最后一层中间的那个点

2)当数字三角形有偶数行时，我们需要走奇数步，所以左移和右移步数差绝对值一定为1，最后一定走到最后一层中间两个点中的一个

因此可以得出N%21时从(N,N/2+1)开始向上搜索，N%20时，从(N,N/2),(N,N/2+1)开始向上搜索取其中大的那个

我们仅需要从底层的目标点向上进行搜索，并且在搜索过程中不用考虑步数限制

他人题解

#pragma optimize(1)
#pragma optimize(2)
#pragma optimize(3,"Ofast","inline")
#include
#include
#include
using namespace std;
int N;//表示数字三角形行数 
int ans=0;//存储搜索结果 
int triangle[101][101]={0};//存储数字三角形
int dp[101][101]={0};//dp[i][j]表示从数字三角形第i行第j列到顶端的最大路径 
int MAX_route(int i,int j){//求 数字三角形第i行第j列到顶端的最大路径 
    //记忆化递归 ,从底层开始向上搜索 
    if(i==1) return triangle[1][1];//递归到顶端直接返回顶端值 
    if(dp[i][j]!=0) return dp[i][j];// 该值已计算出，直接返回备忘录的值 
    int left=-1,right=-1;//left代表往左上点的最大路径，right代表右上点的最大路径，默认为-1 因为要取max
    if(i!=1){//存在左上路径 
        left=MAX_route(i-1,j-1);//递归左上注意边界条件
    } 
    if(i!=j){//存在右上路径 
        right=MAX_route(i-1,j); 
    }
    dp[i][j]=max(left,right)+triangle[i][j];
    return dp[i][j];
}
int main(){
    cin>>N;
    for(int i=1;i<=N;++i){
        for(int j=1;j<=i;++j){
            cin>>triangle[i][j];
        }
    } 
    if(N%2){//奇数行的数字三角形 
        ans=MAX_route(N,N/2+1); 
    }
    else{
        ans=max(MAX_route(N,N/2),MAX_route(N,N/2+1));
    }
    cout<<ans;
    return 0;
    }

我自己改了一下代码，更加容易理解，注意是倒着搜的！因为这样终点只会是顶端 i==1，而起点有两种情况

#pragma optimize(1)
#pragma optimize(2)
#pragma optimize(3,"Ofast","inline")
#include
#include
#include
using namespace std;
int N;//表示数字三角形行数
int ans=0;//存储搜索结果
int triangle[101][101]={0};//存储数字三角形
int dp[101][101]={0};//dp[i][j]表示从数字三角形第i行第j列到顶端的最大路径
int MAX_route(int i,int j){//求 数字三角形第i行第j列到顶端的最大路径
    //记忆化递归 ,从底层开始向上搜索
    if(i==1) return triangle[1][1];//递归到顶端直接返回顶端值
    if(dp[i][j]!=0) return dp[i][j];// 该值已计算出，直接返回
    int left=-1,right=-1;//left代表往左上点的最大路径，right代表右上点的最大路径

    for(int a=2;a<=i;a++){
        for(int b =1;b<=j;b++){
            if(a==b){
                dp[i][j]= MAX_route(i-1,j-1)+triangle[i][j];
            }
            else{
                dp[i][j]=max(MAX_route(i-1,j-1),MAX_route(i-1,j))+triangle[i][j];
            }
        }
    }
    return dp[i][j];
}
int main(){
    cin>>N;
    for(int i=1;i<=N;++i){
        for(int j=1;j<=i;++j){
            cin>>triangle[i][j];
        }
    }
    if(N%2){//奇数行的数字三角形
        ans=MAX_route(N,N/2+1);
    }
    else{
        ans=max(MAX_route(N,N/2),MAX_route(N,N/2+1));
    }
    cout<<ans;
    return 0;
}

方法三：dp+找规律

一般能用dp就用dp ，别搜

要考虑向左下走的次数与向右下走的次数相差不能超过 1，肯定存在一定的规律，推一下！（写几条路径找一下规律）

画一下就能知道，这样画的结果最后一定会落在最后一行的中间，如果是奇数行，那就是最中间那个，偶数行就找中间两个比较大的数就可以了

n=int(input())
a=[[0]*(n) for i in range(n)]
for i in range(n):
    row=list(map(int,input().split()))
    a[i]=row
#print(a)
dp=[[0]*(n) for i in range(n)]
dp[0][0]=a[0][0]
for i in range(1,n):
    for j in range(i+1):
        if j ==0:
            dp[i][0] = dp[i-1][0]+a[i][0]
        elif i==j:
            dp[i][j]=dp[i-1][j-1]+a[i][j]
        else:
            dp[i][j]=max(dp[i-1][j-1],dp[i-1][j])+a[i][j]
                
#print(dp)
if n%2==1:
    print(dp[n-1][(n-1)//2])
else :
    print(max(dp[n-1][(n-1)//2],dp[n-1][(n-1)//2+1]))

为了对于三角形，我们dp也不多开，这里就要多考虑一下边界问题，多试几组输入！！ac