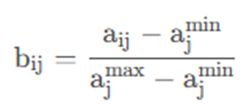数学建模论文分析
文章内容部分引用自:数学建模--数据预处理_派大星先生c的博客-CSDN博客_数学建模比赛的数据怎么预处理
数学建模笔记(三):数据预处理_Yangtze20的博客-CSDN博客_数学建模数据预处理
一、“假设”的作用
合理的模型假设,抛开了一些次要的因素(一些人为不可控因素),抓出主要因素,使用精确的语言对问题进行分析,做出假设
二、数据预处理
数据预处理主要有四个任务: 数据清洗、数据集成、数据变换及数据规约。
常用的是 数据清洗与数据变换,其中数据清洗包括异常值与缺失值的处理;数据变换指将一种格式的数据转换为另一格式的数据。
- 数据残缺
缺失值的处理方法主要有三种:删除记录、数据插补和不处理。
删除记录,顾名思义,指当该组数据某一个案的数据缺省时,删除这组个案的数据,这种方法的优点是处理方便,但在数据较少时要慎重使用。
数据插补,使用不同的插补方法将缺省的数据补齐。主要插补方法有:均值/中位数/众数插补;使用固定值插补;最近邻插补;回归方法插补;插值法插补。
最近邻插补:即在记录中找到与缺失样本最接近的样本的该属性插补,可以通过计算对象间的欧式距离衡量。
回归方法插补:根据已有数据和与其有关的其他变量的数据建立拟合模型来预测缺失值。
插值法:常用的插值方法有很多,下面我列出一些。
不处理,有时我们可以将所有缺省数据的样本划分为另一组,进行特殊处理。
①插值
对于一维曲线的插值,一般用到的函数yi=interp1(X,Y,xi,method) ,其中method包括nearst,linear,spline,cubic。
‘nearest’——最邻近插值:插入与其距离最近的值
‘linear’——线性插值:构造线性函数进行插值
‘spline’——三次样条插值:将定义域分成若干个区间,在每个区间内构造三次多项式进行插值
‘cubic’——立方插值:构造立方函数进行插值
ps:‘method’缺省时默认为线性插值对于二维曲面的插值,一般用到的函数zi=interp2(X,Y,Z,xi,yi,method),其中method也和上面一样,常用的是cubic。
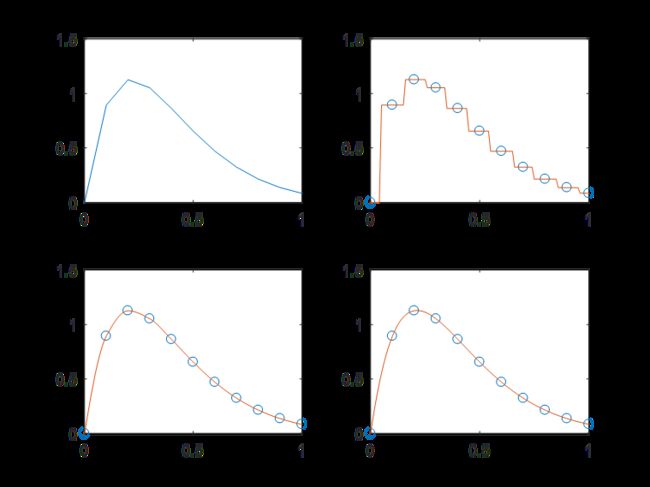
%产生原始数据
x=0:0.1:1;
y=(x.^2-3*x+7).*exp(-4*x).*sin(2*x);
subplot(2,2,1);
plot(x,y);
title('原始数据');
%线性插值
xx=0:0.01:1;
y1=interp1(x,y,xx,'linear');
%subplot(2,2,1)
%plot(x,y,'o',xx,y1);
%title('线性插值');
%最邻近点插值
y2=interp1(x,y,xx,'nearest');
subplot(2,2,2)
plot(x,y,'o',xx,y2);
title('最邻近点插值');
%三次插值
y3=interp1(x,y,xx,'pchip');
subplot(2,2,3)
plot(x,y,'o',xx,y3);
title('三次插值');
%三次样条插值
y4=interp1(x,y,xx,'spline');
subplot(2,2,4)
plot(x,y,'o',xx,y4);
title('三次样条插值');利用给定的高度补充地图
%插值基点为网格节点
clear all
y=20:-1:0;
x=0:20;
z=[0.2 0.2 0.2 0.2 0.2 0.2 0.4 0.4 0.3 0.2 0.3 0.2 0.1 0.2 0.2 0.4 0.3 0.2 0.2 0.2 0.2;
0.3 0.2 0.2 0.2 0.2 0.4 0.3 0.3 0.3 0.3 0.4 0.2 0.2 0.2 0.2 0.4 0.4 0.4 0.3 0.2 0.2;
0.2 0.3 0.3 0.2 0.3 1 0.4 0.5 0.3 0.3 0.3 0.3 0.2 0.2 0.2 0.6 0.5 0.4 0.4 0.2 0.2;
0.2 0.2 0.4 0.2 1 1.1 0.9 0.4 0.3 0.3 0.5 0.3 0.2 0.2 0.2 0.7 0.3 0.6 0.6 0.3 0.4;
0.2 0.2 0.9 0.7 1 1 1 0.7 0.5 0.3 0.2 0.2 0.2 0.6 0.2 0.8 0.7 0.9 0.5 0.5 0.4;
0.2 0.3 1 1 1 1.2 1 1.1 0.8 0.3 0.2 0.2 0.2 0.5 0.3 0.6 0.6 0.8 0.7 0.6 0.5;
0.2 0.4 1 1 1.1 1.1 1.1 1.1 0.6 0.3 0.4 0.4 0.2 0.7 0.5 0.9 0.7 0.4 0.9 0.8 0.3;
0.2 0.2 0.9 1.1 1.2 1.2 1.1 1.1 0.6 0.3 0.5 0.3 0.2 0.4 0.3 0.7 1 0.7 1.2 0.8 0.4;
0.2 0.3 0.4 0.9 1.1 1 1.1 1.1 0.7 0.4 0.4 0.4 0.3 0.5 0.5 0.8 1.1 0.8 1.1 0.9 0.3;
0.3 0.3 0.5 1.2 1.2 1.1 1 1.2 0.9 0.5 0.6 0.4 0.6 0.6 0.3 0.6 1.2 0.8 1 0.8 0.5;
0.3 0.5 0.9 1.1 1.1 1 1.2 1 0.8 0.7 0.5 0.6 0.4 0.5 0.4 1 1.3 0.9 0.9 1 0.8;
0.3 0.5 0.6 1.1 1.2 1 1 1.1 0.9 0.4 0.4 0.5 0.5 0.8 0.6 0.9 1 0.5 0.8 0.8 0.9;
0.4 0.5 0.4 1 1.1 1.2 1 0.9 0.7 0.5 0.6 0.3 0.6 0.4 0.6 1 1 0.6 0.9 1 0.7;
0.3 0.5 0.8 1.1 1.1 1 0.8 0.7 0.7 0.4 0.5 0.4 0.4 0.5 0.4 1.1 1.3 0.7 1 0.7 0.6;
0.3 0.5 0.9 1.1 1 0.7 0.7 0.4 0.6 0.4 0.4 0.3 0.5 0.5 0.3 0.9 1.2 0.8 1 0.8 0.4;
0.2 0.3 0.6 0.9 0.8 0.8 0.6 0.3 0.4 0.5 0.4 0.5 0.4 0.2 0.5 0.5 1.3 0.6 1 0.9 0.3;
0.2 0.3 0.3 0.7 0.6 0.6 0.4 0.2 0.3 0.5 0.8 0.8 0.3 0.2 0.2 0.8 1.3 0.9 0.8 0.8 0.4;
0.2 0.3 0.3 0.6 0.3 0.4 0.3 0.2 0.2 0.3 0.6 0.4 0.3 0.2 0.4 0.3 0.8 0.6 0.7 0.4 0.4;
0.2 0.3 0.4 0.4 0.2 0.2 0.2 0.3 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.5 0.7 0.4 0.4 0.3 0.3;
0.2 0.2 0.3 0.2 0.2 0.3 0.2 0.2 0.2 0.2 0.2 0.1 0.2 0.4 0.3 0.6 0.5 0.3 0.3 0.3 0.2;
0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.4 0.7 0.4 0.2 0.4 0.5 0.5];
%未插值直接画图
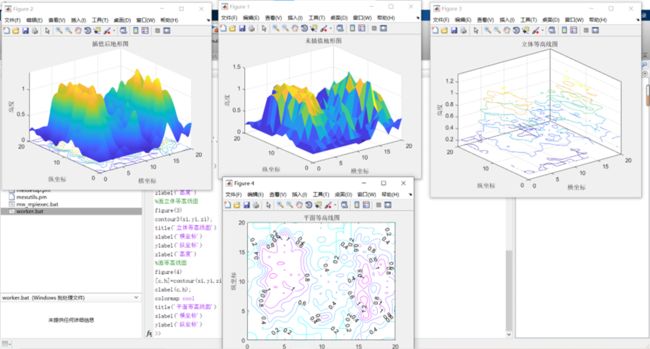
figure(1) %创建图形窗口1,并激活
surf(x,y,z);
shading flat %用shading flat命令,使曲面变的光滑
title('未插值地形图')
xlabel('横坐标')
ylabel('纵坐标')
zlabel('高度')
%三次插值后画图
%画地形图
figure(2)
xi=0:0.05:20;
yi=20:-0.05:0;
zi=interp2(x,y,z,xi',yi,'cubic'); %'cubic'三次插值
surfc(xi,yi,zi); %底面带等高线
shading flat
title('插值后地形图')
xlabel('横坐标')
ylabel('纵坐标')
zlabel('高度')
%画立体等高线图
figure(3)
contour3(xi,yi,zi);
title('立体等高线图')
xlabel('横坐标')
ylabel('纵坐标')
zlabel('高度')
%画等高线图
figure(4)
[c,h]=contour(xi,yi,zi);
clabel(c,h); %用于为2维等高线添加标签
colormap cool %冷色调
title('平面等高线图')
xlabel('横坐标')
ylabel('纵坐标')散乱点插值
当插值点(x,y)为散乱点,不再是网格上的点时,可以使用griddata命令进行二维插值:
griddata(x,y,z,xi,yi,'method')%'method'用法同上②拟合
对于一维曲线的拟合,一般用到的函数p=polyfit(x,y,n)和yi=polyval(p,xi),这个是最常用的最小二乘法的拟合方法。
对于二维曲面的拟合,有很多方法可以实现,这里运用Spline Toolbox里面的函数功能。
x = 0:0.1:1;
y = [-0.447 1.9783.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];
A = polyfit(x,y,2) %A为拟合出来的函数
z =polyval(A,x); %求多项式在x处的值z
plot(x,y,'k+',x,z,'r')③邻近替换
前/后一个非缺失值将其替换
最近的非缺失值替换
相邻的非离群值线性插值填充test_data1=fillmissing(test_data,'previous');
test_data1=fillmissing(test_data,'next');
test_data1=fillmissing(test_data,'nearest');
test_data1=fillmissing(test_data,'linear');2、异常值处理
异常值的处理方法较为简单,主要方法有: 删除记录、视为缺失值、平均值修正和不处理。由于处理异常值的方法简单,在此不作解释。
发现异常值是处理异常值的难点,发现异常值主要有两个方法:3σ 原则(拉依达方法就是3σ原则)和画箱型图。
拉依达准则
拉依达准则是用来发现数据异常值
x=[1, 1.1, 1.2, 1.3,1.4, 2, 1.2, 1.3, 1.5, 0.9, 0.8, 1.1, 11];
inlier = [];outlier= [];
len = length(x);
average1 =mean(x); % x中所有元素的均值
standard1 =std(x); % x的标准差
for i = 1:len % 遍历x向量,判断是否为偏离点,不是偏离点则存入inline
if abs(x(i)-average1)= standard2*3
outlier = [outlier x(i)];
end
end 关于异常值剔除,这篇文章写的很详细:菜鸟进阶系列·MATLAB数学建模·数据预处理(一)剔除异常值及平滑处理 - 哔哩哔哩(bilibili.com)
3、数据变换
这部分内容摘自:数学建模笔记(三):数据预处理_Yangtze20的博客-CSDN博客_数学建模数据预处理
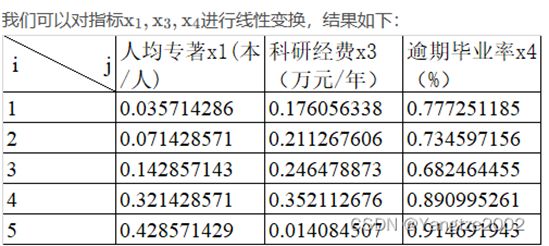
- 线性变换
a = [0.1 50004.7;0.2 6000 5.6;0.4 7000 6.7;0.9 10000 2.3;1.2 400 1.8];
[m,n]=size(a)
for j=1:n
b(:,j)=a(:,j)/sum(a(:,j));
end
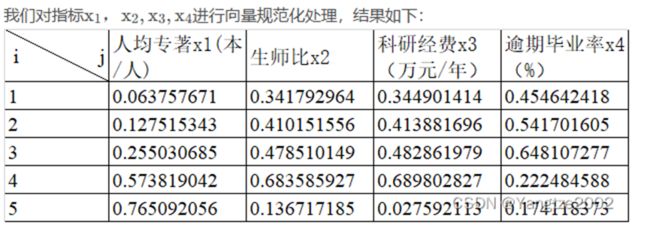
b(:,3)=1-b(:,3);%成本型指标正向化2. 向量规范化
无论xj为效益型指标或成本型指标,均进行如下变换
这种变换也是线性的,但它无法分辨属性值的优劣。它的最大特点是,规范化后各方案的同一指标的平方和为1,因此常用于计算各方案与某种虚拟方案(如理想点或负理想点)的欧氏距离的场合。经过向量规范化处理后的数据在[-1,1]区间内。
a = [0.1 5 50004.7;0.2 6 6000 5.6;0.4 7 7000 6.7;0.9 10 10000 2.3;1.2 2 400 1.8];
[m,n]=size(a)
for j=1:n
b(:,j)=a(:,j)/norm(a(:,j));
end3.min-max归一化
在实际问题中,不同变量的测量单位往往是不一样的。为了消除变量的量纲效应,使每个变量都具有同等的表现力,通常可以通过这种方式对数据去量纲化。
若xj为效益型指标,令
a = [0.1 5 50004.7;0.2 6 6000 5.6;0.4 7 7000 6.7;0.9 10 10000 2.3;1.2 2 400 1.8];
[m,n]=size(a)
x2=@(qujian,lb,ub,x)(1-(qujian(1)-x)./(qujian(1)-lb)).*(x>=lb&x=qujian(1)&x<=qujian(2))+(1-(x-qujian(2))./(ub-qujian(2))).*...
(x>qujian(2)&x<=ub);%利用函数句柄转换区间型变量
qujian=[5,6];lb=2;ub=12;
a(:,2)=x2(qujian,lb,ub,a(:,2));
A=[a(:,1) a(:,3)a(:,4)];
A=maxmin(A);%maxmin为自定义的归一化函数
b=[A(:,1) a(:,2)A(:,2) A(:,3)];
%{
%对数据进行归一化函数
functionnew=maxmin(old)
%找出每列的最大最小值
maxold=max(old);
minold=min(old);
%张成与old一样大小,主要对行进行复制,列不用变
m=size(old,1);
maxnew=repmat(maxold,m,1);
minnew=repmat(minold,m,1);
new=(old-minnew)./(maxnew-minnew);
end
%} 4.z-score标准化
这也是另一种较为常用的数据去量纲化的处理方式,将原始数据作如下变换
a = [0.1 5 5000 4.7;0.2 6 6000 5.6;0.4 7 7000 6.7;0.9 10 10000 2.3;1.2 2 400 1.8];
b=zscore(a);%将每组数据按列标准化三、模型建立与求解(以ARIMA模型为例)
1、模型的描述(列公式)(写原理)
2、模型参数的确定(matlab/SPSS)
p,d,q值的确定
3、结果分析,进行预测
四、模型分析
五、模型结果检验
六、模型评估