R语言逻辑回归详细代码：预测双十一顾客是否使用天猫优惠券

R语言逻辑回归详细代码：预测双十一顾客是否使用天猫优惠券

#[1,] “age” 年龄
#[2,] “job” 工作
#[3,] “marital” 婚姻状况
#[4,] “default” 花呗是否违约
#[5,] “returned” 是否有过退货
#[6,] “loan” 是否使用花呗结账
#[7,] “coupon_used_in_last6_month” 过去六个月优惠券使用数量
#[8,] “coupon_used_in_last_month” 过去一个月优惠券使用数量
#[9,] “coupon_ind” 本次活动中是否使用优惠券
数据源链接，提取码：1ib7

rm(list = ls())

#导入数据--------------------

data = read.csv(‘天猫优惠券.csv’,colClasses = c(‘integer’,‘integer’,‘factor’,‘factor’,
‘factor’,‘factor’,‘factor’,‘integer’,‘integer’,‘numeric’))
data1 = data[,-1]
#定义目标值
target = data$coupon_ind
class(target)
#数据清洗--------------------
#找出是否有缺失值变量
nanumber = sapply(data,function(x)sum(is.na(x)))
summary(nanumber)
nanumber

#五数图
summary(data1)

#提取列名
as.matrix(colnames(data1))
#进一步筛选变量--------------

#计算x1的IV值 IV表示衡量变量预测能力 WOE衡量变量某个属性的区分能力
x1= data1$age
hist(x1)
x1 = binning(x1,bins = 8,method = ‘quantile’)
temp1 = table(x1,target)
temp1
#将频数统计表转化为数据框，矩阵的长度为水平的个数
temp2 = as.data.frame(matrix(temp1,length(unique(x1)),2))
temp2
#计算比例
temp3 = sapply(temp2,function(x) x/sum(x))
temp3

woe = log(temp3[,2]/temp3[,1])*100

iv = sum((temp3[,2]-temp3[,1])*woe)

#由单变量iv值扩展到所有自变量iv值
var.iv = function(x,target){
if(is.factor(x))
{ #做出频数统计表
temp4 = table(x,target)
#转化为数据框形式
temp5 = as.data.frame(matrix(temp4,length(unique(x)),2))
#计算比例
temp6 = sapply(temp5,function(x) x/sum(x))
woe = log(temp6[,2]/temp6[,1])*100
iv = sum((temp6[,2]-temp6[,1])[!is.infinite(woe)]*woe[!is.infinite(woe)])
}
#如果x是数值型，则对其分组，分为8段，按照分位数分
if(is.integer(x))
{
x= binning(x,bin = 8,method = ‘quantile’)
#做出频数统计表
temp1 = table(x,target)
#转化为数据框形式
temp2 = as.data.frame(matrix(temp1,length(unique(x)),2))
#计算比例
temp3 = sapply(temp2,function(x) x/sum(x))
#如果有不是矩阵的，则直接默认iv为0
if(!is.matrix(temp3)) {iv = 0} else
{
woe = log(temp3[,2]/temp3[,1])*100
iv = sum((temp3[,2]-temp3[,1])[!is.infinite(woe)]*woe[!is.infinite(woe)])
}
}
return(iv)
}

#利用自编函数验证x值
var.iv(data$age,data$coupon_ind)
var.iv(data$job,data$coupon_ind)
#检查所有自变量的iv值
iv.value = sapply(data1[,-9],function(x)var.iv(x,data1$coupon_ind))
summary(iv.value) #查看筛选变量阀点

#由于变量较少,因此筛选IV值大于2的变量
input = names(which(iv.value>2))
length(input)

##确定最终进入模型的变量——————————————————————————

#数据整理
data1_input = data1[,input]
n=nrow(data1_input)

#分割数据：训练样本和测试样本
set.seed(1234)

#随机抽样序号
train_number = sample(1:n,round(n*0.8))

#构造训练集
train_x = data1_input[train_number,]

train_y = data[train_number,‘coupon_ind’]

table(train_y)

train = data.frame(train_y,train_x)

#构造测试集
test_x = data1_input[-train_number,]
test_y = data[-train_number,‘coupon_ind’]

table(test_y)

#查看训练接数据
str(train_y)
str(train_x)

#建立广义逻辑回归模型————————————————————————------------------------------
logitfit = glm(train_y~.,data = train,family = ‘binomial’)

summary(logitfit)

#查看模型参数
coef(logitfit)

#系数的含义其实是优势比的增加量 实际上指的是1和0的相对风险 如下是为了更方便看出数值大小

sapply(coef(logitfit),function(x) round(exp(x),3))

##模型评估——————————————————————

#过度离势 overdispersion = 残差偏差/残差自由度，若大于1，则表明参数检验精度下降

overdispersion = logitfit$deviance/logitfit$df.residual
overdispersion

#逐步回归，删除相关性强的变量
logitfitstep = step(logitfit)

#检验回归后的模型各自的系数是不是同时为0。H0:所有系数均为0
anova(logitfitstep,test = ‘Chisq’)

#查看模型参数
coef(logitfitstep)

#逐步回归后构建新的模型
logitfit = glm(train_y ~ job + marital + returned + loan +
coupon_used_in_last6_month +
coupon_used_in_last_month,data = train,family = ‘binomial’)
summary(logitfit)

summary(logitfit)

#VIF 方差膨胀因子检验 查看是否还存在多重共线性，一般的：当VIF^1/2>2表明存在多重共线性
vif(logitfit)
sqrt(vif(logitfit))>2

#模型预测-----------------------------

logit_fitted_train = logitfit$fitted.values

logit_fitted_test1 = predict(logitfit,newdata = test_x,type = ‘response’)

#找出概率临界值，以此区分优惠券是否响应-----------------------------------

#样本内聚类，样本内0和1的概率
p = table(train_y)/length(train_y)

#以p[2]作为临界值划分
logit.cluster = factor(logit_fitted_train >p[2],levels = c(F,T),
labels = c(0,1))
#查看分类结果
table(logit.cluster)

#训练集预测准确率
pre.pre.train = table(train_y,logit.cluster,dnn = c(‘Actual’,‘Predicted’))

p11 = pre.pre.train[2,2]/sum(pre.pre.train[2,]) #优惠券使用命中率,真正率

p12 = pre.pre.train[1,1]/sum(pre.pre.train[1,]) #优惠券未使用命中率,真负率

accuracy = (pre.pre.train[1,1]+pre.pre.train[2,2])/sum(pre.pre.train) #整个模型的预测准确率

#样本外预测

#逻辑分类
logit.pred = factor(logit_fitted_test1 >p[2],levels = c(F,T),
labels = c(0,1))

table(logit.pred)

#对比预测和真实值

table_pre.test = table(test_y,logit.pred,dnn = c(‘Actuall’,‘Predicted’))

#测试集0和1的正确率
accuracy = (table_pre.test[1,1]+table_pre.test[2,2])/sum(table_pre.test)

#上述的临界值是根据训练集数据得出的，主观性较强，根据最终目的,我们是想找提高模型预测精度，
#然后对优惠券做对应的商业活动，所以真正率和真负率之间的取值需要权衡
#下面画roc曲线和lift曲线
#roc曲线
modelroc = roc(test_y,logit_fitted_test1,plot =TRUE) #横轴为真负率，纵轴为真正率

plot(modelroc,print.auc = TRUE,auc.polygon = TRUE,grid = c(0.1,0.2),
grid.col = c(‘green’,‘red’),max.auc.polygon = TRUE,
auc.polygon.col = ‘skyblue’,print.thres = TRUE)
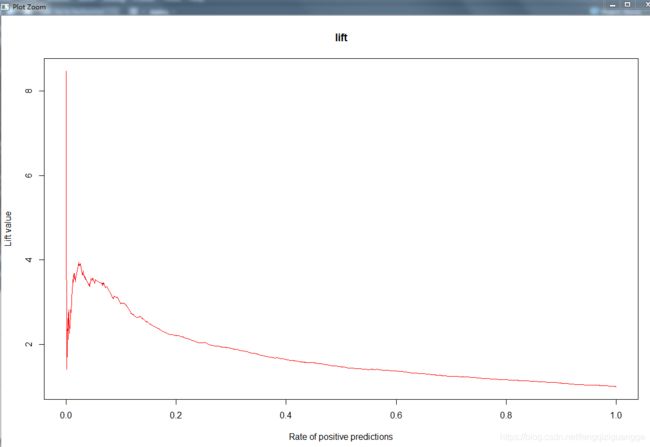
#lift曲线
pr = prediction(logit_fitted_test1,test_y)
plot(performance(pr,‘lift’,‘rpp’),col = ‘red’,lty = 1,
add = FALSE,main =‘lift’ )

#阀值最终可以取0.137，兼顾提升度、真正率和真负率，最终的训练模型如下，输出0和1
logitfit = glm(train_y ~ job + marital + returned + loan +
coupon_used_in_last6_month +
coupon_used_in_last_month,data = train,family = ‘binomial’)

xin.xn = ifelse(logitfit$fitted.values >0.137,1,0)

roc曲线图

提升度折线图