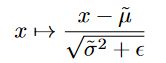【论文阅读】Density estimation using Real NVP

前言

• 博客主页：睡晚不猿序程
• ⌚首发时间：2022.9.17
• ⏰最近更新时间：2022.9.17
• 本文由 睡晚不猿序程 原创，首发于 CSDN
• 作者是蒻蒟本蒟，如果文章里有任何错误或者表述不清，请 tt 我，万分感谢！orz

---

1. 内容简介

论文标题：Density estimation using Real NVP

作者：Jascha Sohl-Dickstein，Samy Bengio

发布于：arXiv 2017

自己认为的关键词：可逆神经网络，图像生成

---

2. 摘要浏览

解决的问题：使用 INN 进行自然图像生成

本文工作：使用了 Real-Valued non-volume preserving（real NVP）变换来得到一个无监督学习的深度学习算法，可以直接进行对数似然计算

架构：real NVP

完成效果：在后文的实验中将这个模型用于了四个数据集的自然图像生成

3. 图片、表格浏览

图一

这个展示的应该是模型推理和生成的过程

这个是在一个 toy 2d 数据上拟合的效果展示，学习到的函数 f 可以将训练数据 x（服从于左上角的分布）映射为隐藏分布中最接近的样本 z。

反过来，其逆函数可以把样本 z 映射到训练数据分布中最接近的样本 x

图二

展示了可逆神经网络的标志特点：耦合层。将输入拆解成为 x1 和 x2，然后先使用一个乘法再进行一个加法计算

这样操作可以让其可逆，并且行列式可以计算

行列式可计算在这个模型是一个重要的特性

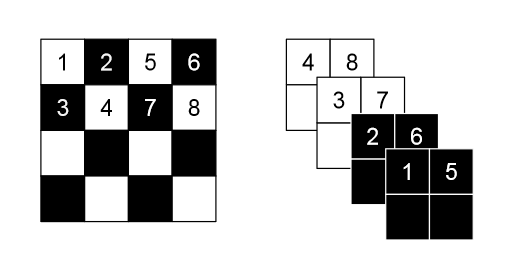
图三

这张图片展示了 Squeezing 操作的过程，他会把一个 $4\times 4\times 1$ 的张量转换为 $2\times 2\times 4$ 的张量 。

按照我的理解，应该是按照黑白两色来进行图像的分解（也就是分为 x1 和 x2），然后按照棋盘分解的方式把图像的维度降低，但是通道增加

去查看了一下相关的资料，确实是这样的，直接输出的部分直接使用 mask 掩盖掉，然后剩余的部分就是要进行处理的部分

看到了一个博客以及一个课程：博客，伯克利CS294-158-SP20 深度无监督学习

图四

左：每次经过一层，就会颠倒 x1，x2 的位置，这样可以让信息充分混合，不会让一部分信息一直无损的通过

右：变量分解，每一次只有一半的变量被直接建模为高斯分布，而其他的变量则需要进一步变换（就像 CNN

一样，这样可以保留多尺度信息？）

表一

bits/dim：一个评价指标，越低越好，

图五

左：用于训练的图像

右：模型生成的图像

图六

流型生成样例

按照我的理解，是不是采样两个 z1，z2 来进行生成，然后通过插值算法让 z1 逐步变为 z2，然后可以呈现上面例子的样子，有一个逐步变化的过程

图片浏览完毕，感觉不是很能理解网络的结构啊

---

4. 引言浏览

整个表征学习的领域正在因为子监督学习技术的发展而经历一场重大的变革。其中一个进行无监督学习的主要方法是生成概率模型。生成概率模型不仅可以创造新的东西，还可以广泛用于重建相关的任务（e.g. 图像修复，去噪，上色，超分）

因为图像是一种高维数据，并且有复杂的结构，所以该领域的难点在于——创建的模型不仅要足够强大，而且还要可以训练。

作者提出了 real NVP 变换，这是一种简单且富有表现力的对高维数据进行建模的方法

---

自由阅读

5. 模型定义（原文第三章）

作者表示，在这篇文章中将会解决在高维连续空间中通过最大化似然学习高度非线性模型的问题。

所得到的 cost function 不依赖于固定形式的 reconstruction cost，因此可以生成锐度更高的样本

这里的 cost 是不是想表达损失？

作者在这个模型上使用了目前最新的方法，例如 BN，残差网络等

5.1 变量公式变化

给出观测数据变量 $x\in X$ ，隐变量 $z\in Z$ 上的一个简单先验概率分布 $p_Z$ ，以及一个双射函数$f:X\to Z$ (其反函数 $g=f^{-1}$）。我们可以用变量代换公式来在 X 上定义一个模型分布

来自结果分布的确切样本可以通过其逆变换采样法则来生成。其中样本 $z\sim p_Z$ 从隐空间中采样，而他的逆图像 $x=f^{-1}(z)=f(z)$ 会生成一个原来样本空间的样本。

计算样本点 x 的概率密度是通过计算其图像$f(x)$ 的概率密度乘以他的雅各布矩阵

这里应该没有说的很清楚，应该就是一个概率公式的变量替换，因为我概率论已经忘得差不多了iai，这里推荐一下李宏毅的视频，他这一块有提到，但是也没有讲过程是怎么样的就是了

害，感觉这个地方真的搞不清楚，这些什么概率密度，变量替换什么的，之后再看吧【落泪】

我来大胆的猜想一下：一个变量的概率密度应该服从一个概率密度函数，它可以在一个二维坐标系表示。然后概率密度函数乘上另一个概率密度函数，这样应该可以生成另一个概率密度函数吧，而且其积分为1。如果是一张图像，他的概率密度应该是高维的（例如 28*28 大小的图像，可以展开成 784 维的向量，这样的概率密度非常难表示）但是同样可以通过变换来生成另一个概率密度

感觉把自己绕的晕乎乎

5.2 耦合层

因为要直接去计算输入矩阵的行列式，这是非常复杂的，因为总总限制就带来了耦合层这种东西

NICE 证明了这个结构的有效性。因为计算在这个变换中雅各布矩阵的行列式对于应用这一法则来训练是至关重要的。

Real NVP 比起 NICE 多增加了一个 s 变换，不仅仅只是做加法了， 多增加了一个乘法计算，这样会导致他的雅各布行列式发生变化，具体底下会有体现

5.3 性质

其一：上面这个是该变换的雅各布矩阵行列式，我们可以看到左上角是一个单位矩阵，右下角因为引入了一个 s 的乘法计算，所以其行列式就是一个前 d 维元素组成的三角矩阵

同样，因为这个矩阵是对角矩阵，所以行列式很好求，就是对角线元素相乘就可以了

因为 s 和 t 函数可以做的任意复杂，所以它可以包含比其输入更多的信息

其二：这个概率模型可逆。所以采样过程也是非常高效的。

5.4 掩盖卷积

划分操作可以简单的使用 mask 来进行划分，如以下公式：

其中 b 是一个张量，其值仅为 0 和 1，这样可以高效的进行划分

作者使用了两种划分方式来利用图像的局部空间结构：一种是空间棋盘法，另一种是通道掩盖（channel-wise mask）

应该是两种划分方式，一种是左边，拆成两个通道。一种是右边，先缩小变成四个通道，然后再进行划分

一个划分的是像素（一个像素位置可能有多个通道），另一个划分的是通道

这里还讲了一个 squeezing 操作，就是先做一次棋盘变换，然后在做一次通道掩盖

5.5 组合耦合层

因为每一次划分都会有一半的数据没有变化，所以再下一个划分的时候就需要让划分之后的数据的角色对调一下，让数据充分的混合

5.6 多尺度结构

作者使用了上面描述的 squeezing 操作来实现，这个操作会把 $s\times s\times c$ 的张量变换为 $s/2\times s/2\times 4c$ 的张量，可以有效的使用空间大小来换通道数量

在每一个尺度，作者将多个操作组成一个序列，例如：

首先，使用三个耦合层，并且使用棋盘掩盖

接着做一个 squeezing 操作

最后使用三个耦合层，使用通道掩盖

因为直接将 D 维度的向量通过耦合层进行建模的开销较大，所以作者他们采取了一种方法，每次只会有一半的数据被建模

就是，拆成四个通道，通过卷积耦合层，一半直接输出，另一半继续通过卷积耦合层，以此类推

5.7 批量归一化

作者使用 ResNet 作为 s 和 t，并且使用了 Batch Norm 以及 weight norm

这里使用的是 BN 的变体？基于小批量处运行的平均值。

不仅在 s 和 t 上有 BN，每一个耦合层的输出也接上了 BN，使用了 BN 也可以轻松计算雅克布矩阵行列式，因为 BN 就像在每一个维度上做了一个线性缩放，如下：

其雅各布矩阵行列式

我也不去想这是怎么来的了，我永远也想不明白iai，这是得什么样的脑子才能做到这种操作啊啊啊啊

5.8 总结

这一节真的太难读了，单词不懂，句子也看不懂，真的是无语

重新梳理一下这里讲的东西

1. 耦合层

这个应该好理解一点，就是将输入拆成两个部分，然后进行计算耦合

2. Mask

这里提到了两种 mask

1. spatial checkerboard mask（棋盘掩盖）
2. channel wise mask（通道掩盖）

棋盘掩盖：用来划分输入，让操作变得简单，只需要一个矩阵按元素乘法就可以实现

通道掩盖：我觉得是用来为后面的多尺度服务的，用来划分通道

3. Multi-scale architecture

多尺度结构，看的真的云里雾里

squeezing：他会把减小分辨率，提高通道数

layer：每一层的结构，由三个线性耦合层（checkerboard mask）-squeezing-三个线性耦合层（channel mask）

模型最后一层：四个线性耦合层（checkerboard mask）

大概明白了，这两个mask是两种划分的方式，一种是对像素划分，一种是对通道划分

多个 layer 堆叠成为 multi-scale

for coupling in self.in_couplings:
    # 3x coupling (checkboard)
    x, sldj = coupling(x, sldj, reverse) # sldj is log-determinant jacobian, ignore

if not self.is_last_block:
    # Squeeze -> 3x coupling (channel-wise)
    x = squeeze_2x2(x, reverse=False) # squeeze as mentioned above
    for coupling in self.out_couplings:
        x, sldj = coupling(x, sldj, reverse)
    x = squeeze_2x2(x, reverse=True) # unsqueeze to original shape

    # Re-squeeze -> split -> next block
    x = squeeze_2x2(x, reverse=False, alt_order=True) # 这个squeeze(alt_order=True)我没看懂是在干嘛, 总之到这里scale是halved
    x, x_split = x.chunk(2, dim=1) # 如公式(14), # 把channel分成两半
    x, sldj = self.next_block(x, sldj, reverse), # 一半进入下一个block(递归)
    x = torch.cat((x, x_split), dim=1) # 下一个block输出的结果(尺度没变)和另一半cat起来
    x = squeeze_2x2(x, reverse=True, alt_order=True) # 最终结果unsqueeze回原先的scale

来看一下源码，真的是好蛋疼哦

首先，应该就是使用 squeezing 操作扩充通道数，然后一半输出，另一半接着继续进行处理（使用递归）

害，真的是难理解

以上参考知乎 参考资料

6. 总结、预告

6.1 总结

巧了，还真的是没什么好总结的了，这篇论文的细节太多，数学推理也没有写的非常的明白，相比起之前的 NICE 已经读的头晕晕，现在这篇文章简直就是难度超级加倍，而且文中的语法也不好读懂，属实是有点裂开来了。

那我只能比较一下他和 NICE 之间的区别了，也就是这篇论文做出的改进

1. 增加了乘性的耦合
   NICE 中仅使用了加性耦合，在这 Real NVP 中，加入了一个乘性的耦合，可以对输入的另一部分进行缩放
2. 使用了卷积
   NICE 中仅仅使用了简单的全连接网络作为耦合函数（这个词是我自己创造的哈哈哈）Real NVP 采用了 ResNet 作为其 backbone
3. 多尺度
   引入了一种多尺度的方式，每一次只有一半的输入会被转换为输出，另一半输入递归执行转换
4. BN
   引入了 BN 层，提升效果

6.2 预告

果然，真的是越基础的越不好理解，感觉我这里也没讲明白这是怎么一回事，真的是不好意思iai

所以，要学习的还有好多呢