R语言logistic回归交互项（交互作用）的可视化分析3

既往我们对logistic回归交互项（交互作用）进行了可视化分析，很多人对交互作用影响还不是很明白，都在后台发私信询问。其实交互作用就是一个变量通过对另一个变量的影响，导致结局变量改变,最常见的就是我们药物之间的交互作用，比如β受体阻滞剂对血糖有影响，同时和降糖药使用可能会加强或者减弱降糖药的降糖效果，这就是交互作用。
通常分类和连续变量之间的交互作用可以解释为分类变量斜率的变化，
继续使用我们的不孕症数据（公众号回复：不孕症可以获得该数据）来演示。
先导入数据

library(rms)
bc<-read.csv("E:/r/test/buyunzheng.csv",sep=',',header=TRUE)

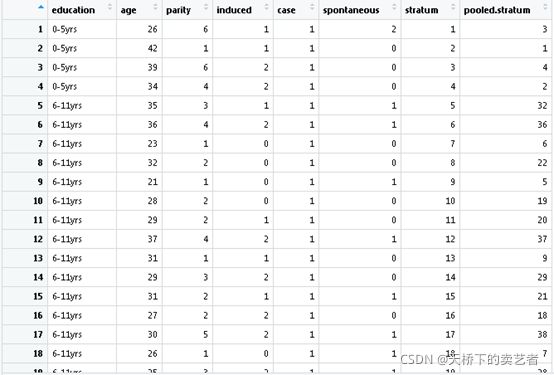
数据有8个指标，最后两个是PSM匹配结果，我们不用理他，其余六个为：
Education：教育程度，age:年龄，parity产次，induced：人流次数，case：是否不孕，这是结局指标，spontaneous：自然流产次数。
有一些变量是分类变量，我们需要把它转换一下

bc$education<-ifelse(bc$education=="0-5yrs",0,ifelse(bc$education=="6-11yrs",1,2))
bc$spontaneous<-as.factor(bc$spontaneous)
bc$case<-as.factor(bc$case)
bc$induced<-as.factor(bc$induced)
bc$education<-as.factor(bc$education)

建立模型，假如我们想知道流产和年龄这两个指标是不是存在交互影响

f1<- glm(case ~ age+spontaneous+age:spontaneous,
         family = binomial(link = logit), data = bc)
summary(f1)

通过拟合模型我们可以把方程式写出来，我们在这里使用冒号（：）来表示交互项
：
Y=-0.92912+age×-0.01455
+（-0.70606×spontaneous1）
+（-0.45443×spontaneous1）
+（0.06040×age:spontaneous1）
+（0.08028×age:spontaneous2）
我们得出方程后就可以根据不同类型的变量，写出拟合模型
对于没有流产的患者:
Y=-0.92912+age×-0.01455
对于流产1次的患者
Y=-0.92912+（age×-0.01455）-1.63517989 +0.06040×age
= -1.635 +0.04584×age
对于流产2次以上的患者
Y=-0.92912+（age×-0.01455）-0.45443 + 0.08028×age
=-1.384+0.0657×age
由此我们得出了每个类型流产对应的不孕症患者的Y的系数，我们也可以通过R来计算这些参数

dia<-coef(f1)
dia

没有流产的患者

small<-c(dia[1],dia[2])
small

流产1次的患者

med<-c(dia[1]+dia[3],dia[2]+dia[5])
med

流产2次以上的患者

lar<-c(dia[1]+dia[4],dia[2]+dia[6])
lar

得出了系数，我们就可以进行数据作图，显示交互作用
先生成预测值

bb<-predict(f1,newdata = bc,type = "link",se =T)

然后进行绘图

cols<-c("black","red","green")###设定颜色
plot(bb$fit~bc$age,col=cols[bc$spontaneous],cex=0.5) ###绘图
abline(coef = small,lwd=2,col="black")##添加线条
abline(coef = med,lwd=2,col="red")##添加线条
abline(coef = lar,lwd=2,col="green")##添加线条
legend("topright",legend = c("spontaneous0","spontaneous1","spontaneous2"),
       lty = 1,lwd = 3,col = cols) ##图例

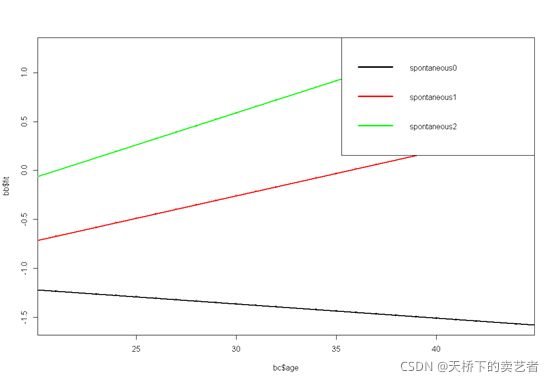
图片还可以进一步修饰，如调整线条和图例位置等，我这里就不弄了，如图所示随着年龄增长，自然流产2次以上的患者不孕的概率比没有自然流产的患者明显增高。