1013门控循环单元GRU

• GRU 是最近几年提出来的,在 LSTM 之后,是一个稍微简化的变体,通常能够提供同等的效果,并且计算速度更快

在某些情况下,希望存在某些机制能够实现:

• 希望某些机制能够在一个记忆元里存储重要的早期信息
• 希望某些机制能够跳过隐状态表示中的此类词元
• 希望某些机制能够重置内部状态表示

做 RNN 的时候处理不了太长的序列

• 因为序列信息全部放在隐藏状态中,当时间到达一定长度的时候,隐藏状态中会累积过多的信息,不利于相对靠前的信息的抽取

在观察一个序列的时候,不是每个观察值都同等重要

• 对于一个猫的图片的序列突然出现一只老鼠,老鼠的出现很重要,第一次出现猫也很重要,但是之后再出现猫就不那么重要了
• 在一个句子中,可能只是一些关键字或者关键句比较重要
• 视频处理中,其实帧与帧之间很多时候都差不多,但是在切换场景的时候,每次的切换是比较重要的

在 RNN 中没有特别关心某些地方的机制,对于它来讲仅仅是一个序列,而门控循环单元可以通过一些额外的控制单元,使得在构造隐藏状态的时候能够挑选出相对来说更加重要的部分(注意力机制在这方面强调得更多一点)

• 更新门(update gate):能关注的机制,能够将信息尽量放在隐藏状态中,控制新状态中有多少个是旧状态的副本
• 重置门(reset gate):能遗忘的机制,能够遗忘输入或者隐藏状态中的一些信息,控制"可能还想记住"的过去状态的数量

门

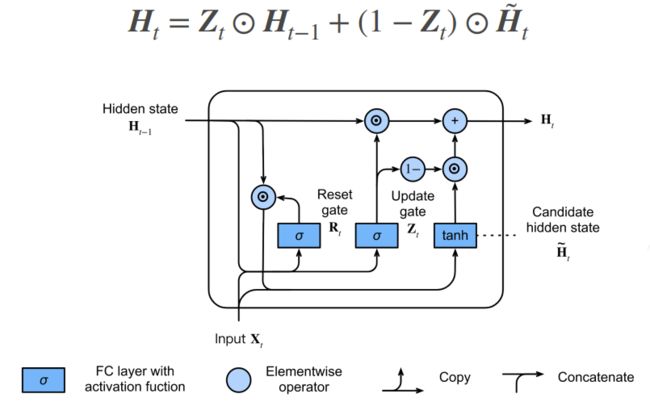
• 上图表示门控循环单元模型,输入是由当前时间步的输入和前一时间步的隐状态给出;重置门和更新门的输出是由使用 sigmoid 激活函数的两个全连接层给出
• Xt :输入
• H(t-1):隐藏状态
• Rt :重置门.如果是 RNN 的话,所表示的是使用 sigmoid 作为激活函数对应的隐藏状态的计算
• Zt :更新门.计算方式和 RNN 中隐藏状态以及 Rt 的计算方式是一样的
• 门可以认为是和隐藏状态同样长度的向量,它的计算方式和 RNN 中隐藏状态的计算方式是一样的

候选隐状态(candidate hidden state)

• 并不是真正的隐藏状态,只是用来生成真正的隐藏状态

• Rt 与 H(t-1) 按元素乘法,对于一个样本来讲, Rt 和 H(t-1)是一个长度相同的向量,所以可以按照元素做乘法
• Rt 是一个取值为 0~1 的值, Rt 越靠近 0 , Rt 与 H(t-1)按元素乘法得到的结果就越接近 0 ,也就相当于将上一时刻的隐藏状态忘掉
• 极端情况下,如果 Rt 全部变成 0 的话,就相当于从当前时刻开始,前面的信息全部不要,隐藏状态变成 0 ,从初始化状态开始,任何预先存在的隐状态都会被重置为默认值
• 另外一个极端情况:如果 Rt 全是 1 的话,就表示,将当前时刻之前所有的信息全部拿过来做更新,就等价于 RNN 中隐藏状态的更新方式
• 实际上 Rt 是一个可以学习的参数,所以它会根据前面的信息来学习哪些信息是能够进入到下一轮隐藏状态的更新,哪一些信息需要进行舍弃,这些操作都是自动进行的,因此被叫做控制单元

隐状态

• 门控循环单元与普通的循环神经网络之间的关键区别在于:前者支持隐状态的门控,这意味着模型有专门的机制来确定应该何时更新隐状态,以及应该何时重置隐状态(这些机制都是可学习的)
• 真正的隐藏状态的计算方式如下所示

• Zt 也是一些取值为 0~1 的一些数字组成的
• 假设 Zt 都等于 1 ,即 Ht 等于 H(t-1),相当于不使用 Xt 来更新隐藏状态,直接将过去的状态当成现在的状态,模型只保留旧状态,此时,来自 Xt 的信息基本上被忽略.当整个子序列的所有时间步的更新门都接近于 1 ,则无论序列的长度如何,在序列起始时间步的旧隐状态都将很容易保留并传递到序列结束
• 假设 Zt 都等于 0 , Ht 等于候选隐状态 Ht tittle .相当于回到了 RNN 的情况,不看过去的隐藏状态,只看现在更新的隐藏状态,能够帮助处理循环神经网络中的梯度消失问题,并且能够更好地捕获时间步距离很长的序列的依赖关系

总结

• GRU 中引入了两个额外的门,每个门可以学习的参数和 RNN 一样多,整个可学习的权重数量是 RNN 的三倍
• Rt 和 Zt 都是控制单元,用来输出取值为 0~1 的数值
• Rt 用来衡量在更新新的隐藏状态的时候,要用到多少过去隐藏状态的信息
• Zt 用来衡量在更新新的隐藏状态的时候,需要用到多少当前Xt相关的信息
• 当 Zt 全为 0 , Rt 全为 1 时,等价于 RNN
• 当 Zt 全为 1 时,直接忽略掉当前 Xt
• GRU 通过引入 Rt 和 Zt ,从而能够在各种极端情况之间进行调整
• 门控循环神经网络可以更好地捕获时间步距离很长的序列上的依赖关系
• 重置门有助于捕获序列中的短期依赖关系
• 更新门有助于捕获序列中的长期依赖关系
• 重置门打开时,门控循环单元包含基本循环神经网络
• 更新门打开时,门控循环单元可以跳过子序列

代码：

import torch
from torch import nn
from d2l import torch as d2l

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

# 初始化模型参数
def get_params(vocab_size, num_hiddens, device):
    num_inputs = num_outputs = vocab_size
    
    def normal(shape):
        return torch.randn(size=shape, device=device) * 0.01
    
    def three():
        return (normal(
            (num_inputs, num_hiddens)), normal((num_hiddens, num_hiddens)),
                torch.zeros(num_hiddens, device=device))
    
    W_xz, W_hz, b_z = three() # GRU多了这两行
    W_xr, W_hr, b_r = three() # GRU多了这两行
    W_xh, W_hh, b_h = three()
    W_hq = normal((num_hiddens, num_outputs))
    b_q = torch.zeros(num_outputs, device=device)
    params = [W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q]
    for param in params:
        param.requires_grad_(True)
    return params

# 定义隐藏状态的初始化函数
def init_gru_state(batch_size, num_hiddens, device):
    return (torch.zeros((batch_size, num_hiddens), device=device),)

# 定义门控循环单元模型
def gru(inputs, state, params):
    W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params     
    H, = state
    outputs = []
    for X in inputs:
        Z = torch.sigmoid((X @ W_xz) + (H @ W_hz) + b_z)
        R = torch.sigmoid((X @ W_xr) + (H @ W_hr) + b_r)
        H_tilda = torch.tanh((X @ W_xh) + ((R * H) @ W_hh) + b_h)
        H = Z * H + (1 - Z) * H_tilda
        Y = H @ W_hq + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H,)

# 训练
vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()
num_epochs, lr = 500, 1
model = d2l.RNNModelScratch(len(vocab), num_hiddens, device, get_params,
                           init_gru_state, gru)
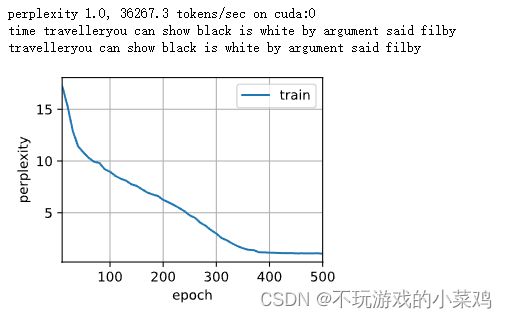
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

 

简洁实现（RNN  GRU）

 

# 简洁实现
num_inputs = vocab_size
gru_layer = nn.RNN(num_inputs, num_hiddens)
model = d2l.RNNModel(gru_layer, len(vocab))
model = model.to(device)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

 

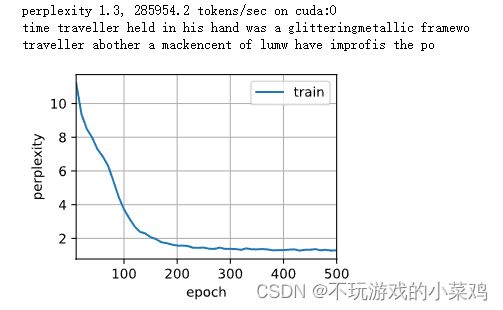
# 简洁实现
num_inputs = vocab_size
gru_layer = nn.GRU(num_inputs, num_hiddens)
model = d2l.RNNModel(gru_layer, len(vocab))
model = model.to(device)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)