项目一 特征衍生实战

【Kaggle】Telco Customer Churn 电信用户流失预测案例

第四部分导读

  在案例的第二、三部分中，我们详细介绍了关于特征工程的各项技术，特征工程技术按照大类来分可以分为数据预处理、特征衍生、特征筛选三部分，其中特征预处理的目的是为了将数据集整理、清洗到可以建模的程度，具体技术包括缺失值处理、异常值处理、数据重编码等，是建模之前必须对数据进行的处理和操作；而特征衍生和特征筛选则更像是一类优化手段，能够帮助模型突破当前数据集建模的效果上界。并且我们在第二部分完整详细的介绍机器学习可解释性模型的训练、优化和解释方法，也就是逻辑回归和决策树模型。并且此前我们也一直以这两种算法为主，来进行各个部分的模型测试。
  而第四部分，我们将开始介绍集成学习的训练和优化的实战技巧，尽管从可解释性角度来说，集成学习的可解释性并不如逻辑回归和决策树，但在大多数建模场景下，集成学习都将获得一个更好的预测结果，这也是目前效果优先的建模场景下最常使用的算法。
  总的来说，本部分内容只有一个目标，那就是借助各类优化方法，抵达每个主流集成学习的效果上界。换而言之，本部分我们将围绕单模优化策略展开详细的探讨，涉及到的具体集成学习包括随机森林、XGBoost、LightGBM、和CatBoost等目前最主流的集成学习算法，而具体的优化策略则包括超参数优化器的使用、特征衍生和筛选方法的使用、单模型自融合方法的使用，这些优化方法也是截至目前，提升单模效果最前沿、最有效、同时也是最复杂的方法。其中有很多较为艰深的理论，也有很多是经验之谈，但无论如何，我们希望能够围绕当前数据集，让每个集成学习算法优化到极限。值得注意的是，在这个过程中，我们会将此前介绍的特征衍生和特征筛选视作是一种模型优化方法，衍生和筛选的效果，一律以模型的最终结果来进行评定。而围绕集成学习进行海量特征衍生和筛选，也才是特征衍生和筛选技术能发挥巨大价值的主战场。
  而在抵达了单模的极限后，我们就会进入到下一阶段，也就是模型融合阶段。需要知道的是，只有单模的效果到达了极限，进一步的多模型融合、甚至多层融合，才是有意义的，才是有效果的。

Part 4.集成算法的训练与优化技巧

# 基础数据科学运算库
import numpy as np
import pandas as pd

# 可视化库
import seaborn as sns
import matplotlib.pyplot as plt

# 时间模块
import time

import warnings
warnings.filterwarnings('ignore')

# sklearn库
# 数据预处理
from sklearn import preprocessing
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OrdinalEncoder
from sklearn.preprocessing import OneHotEncoder

# 实用函数
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score, roc_auc_score
from sklearn.model_selection import train_test_split

# 常用评估器
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression
from sklearn import tree
from sklearn.tree import DecisionTreeClassifier

# 网格搜索
from sklearn.model_selection import GridSearchCV

# 自定义评估器支持模块
from sklearn.base import BaseEstimator, TransformerMixin

# 自定义模块
from telcoFunc import *
# 导入特征衍生模块
import features_creation as fc
from features_creation import *

# re模块相关
import inspect, re

# 其他模块
from tqdm import tqdm
import gc

  然后执行Part 1中的数据清洗相关工作：

# 读取数据
tcc = pd.read_csv('WA_Fn-UseC_-Telco-Customer-Churn.csv')

# 标注连续/离散字段
# 离散字段
category_cols = ['gender', 'SeniorCitizen', 'Partner', 'Dependents',
                'PhoneService', 'MultipleLines', 'InternetService', 'OnlineSecurity', 'OnlineBackup', 
                'DeviceProtection', 'TechSupport', 'StreamingTV', 'StreamingMovies', 'Contract', 'PaperlessBilling',
                'PaymentMethod']

# 连续字段
numeric_cols = ['tenure', 'MonthlyCharges', 'TotalCharges']
 
# 标签
target = 'Churn'

# ID列
ID_col = 'customerID'

# 验证是否划分能完全
assert len(category_cols) + len(numeric_cols) + 2 == tcc.shape[1]

# 连续字段转化
tcc['TotalCharges']= tcc['TotalCharges'].apply(lambda x: x if x!= ' ' else np.nan).astype(float)
tcc['MonthlyCharges'] = tcc['MonthlyCharges'].astype(float)

# 缺失值填补
tcc['TotalCharges'] = tcc['TotalCharges'].fillna(0)

# 标签值手动转化 
tcc['Churn'].replace(to_replace='Yes', value=1, inplace=True)
tcc['Churn'].replace(to_replace='No',  value=0, inplace=True)

features = tcc.drop(columns=[ID_col, target]).copy()
labels = tcc['Churn'].copy()

  同时，创建自然编码后的数据集以及经过时序特征衍生的数据集：

# 划分训练集和测试集
train, test = train_test_split(tcc, random_state=22)

X_train = train.drop(columns=[ID_col, target]).copy()
X_test = test.drop(columns=[ID_col, target]).copy()

y_train = train['Churn'].copy()
y_test = test['Churn'].copy()

X_train_seq = pd.DataFrame()
X_test_seq = pd.DataFrame()

# 年份衍生
X_train_seq['tenure_year'] = ((72 - X_train['tenure']) // 12) + 2014
X_test_seq['tenure_year'] = ((72 - X_test['tenure']) // 12) + 2014

# 月份衍生
X_train_seq['tenure_month'] = (72 - X_train['tenure']) % 12 + 1
X_test_seq['tenure_month'] = (72 - X_test['tenure']) % 12 + 1

# 季度衍生
X_train_seq['tenure_quarter'] = ((X_train_seq['tenure_month']-1) // 3) + 1
X_test_seq['tenure_quarter'] = ((X_test_seq['tenure_month']-1) // 3) + 1

# 独热编码
enc = preprocessing.OneHotEncoder()
enc.fit(X_train_seq)

seq_new = list(X_train_seq.columns)

# 创建带有列名称的独热编码之后的df
X_train_seq = pd.DataFrame(enc.transform(X_train_seq).toarray(), 
                           columns = cate_colName(enc, seq_new, drop=None))

X_test_seq = pd.DataFrame(enc.transform(X_test_seq).toarray(), 
                          columns = cate_colName(enc, seq_new, drop=None))

# 调整index
X_train_seq.index = X_train.index
X_test_seq.index = X_test.index

ord_enc = OrdinalEncoder()
ord_enc.fit(X_train[category_cols])

X_train_OE = pd.DataFrame(ord_enc.transform(X_train[category_cols]), columns=category_cols)
X_train_OE.index = X_train.index
X_train_OE = pd.concat([X_train_OE, X_train[numeric_cols]], axis=1)

X_test_OE = pd.DataFrame(ord_enc.transform(X_test[category_cols]), columns=category_cols)
X_test_OE.index = X_test.index
X_test_OE = pd.concat([X_test_OE, X_test[numeric_cols]], axis=1)

Ch.1 海量特征衍生与筛选

• 海量特征的特征筛选

  在特征筛选的最后一部分，我们开始讨论关于海量特征的特征筛选方法。正如上一小节讨论的一样，建模的目的不同，相应的特征工程策略也会有所不同。而在上一小节中，我们已经详细介绍了关于小量样本情况下的特征筛选方法，而如果是追求建模的最终预测效果，则不可避免会在特征衍生环节通过批量特征衍生来创造大量特征，而此时的特征筛选，也就必然是面对海量特征来进行筛选。
  当然，除了面对的特征数量不同外，效果优先的机器学习建模策略也往往会采用集成学习+模型融合的策略，因此，我们筛选出来的特征也不仅仅是为了单独模型效果服务，而是为了最终融合结果服务。而这样的特征筛选过程，也必然要综合考虑模型融合的建模要求。因此，本节开始也将补充部分模型融合的基础知识，而更多的融合理论及策略，则将在下一部分详细介绍。

• 特征筛选整体流程

  总的来说，模型效果优先的特征衍生和特征筛选并不是割裂的，甚至和模型训练也不是割裂的，而是相互关联、相互穿插的。也就是说我们完全可以按照特征衍生-特征筛选-模型训练-根据模型效果再次进行特征衍生-再次进行特征筛选-再次模型训练等步骤来执行，而在这个过程中，我们往往可以根据下游步骤的结果来调整上游操作，例如可以根据筛选结果调整衍生策略、可以根据模型训练结果调整筛选策略等。也就是说，实际的特征工程和模型训练，并没有完美的、固定的流程，要设计一个行之有效的特征工程和模型训练的策略，还是会比较考验建模工作者的实际经验。

• 特征筛选过程的核心矛盾

  当然，从根据这个流程，我们也不难发现，特征筛选过程的核心矛盾仍然还是效果和效率的平衡，面对海量特征，我们无法做到非常精确的评估（例如是10000个特征最好还是10001个特征最好），当然，考虑到特征衍生环节也没有最优解，因此特征筛选过程寻求这个个证数量的最优解也是毫无意义的。面对最终要执行的模型融合，如何快速的筛选出一批相对高质量的特征，才是核心需要考虑的问题。
  而接下来围绕本案例的数据集进行特征工程和模型训练，则是整个案例阶段的第一次尝试。我们将根据当前数据集的实际情况来设计特征衍生、筛选和模型训练的流程，并最终借助模型融合的方法，达到一个更好的建模效果。

一、基本思路

  首先需要执行的就是特征衍生相关工作，考虑到本数据集样本数量有限，为了更好的做到效果和效率之间的平衡，此处考虑采用更为稳妥的特征衍生策略，即在特征衍生阶段更加侧重衍生特征的质量而非数量，这就需要在衍生的各个阶段配合进行同步的特征筛选相关工作。

• 原始特征的特征筛选

  在实际执行特征衍生之前，我们需要围绕原始特征进行最基础的过滤——也就是缺失值过滤和方差过滤，需要剔除那些缺失值占比极高、或者方差为0的特征。不过根据此前数据探索的结果，原始变量中并不存在这类特征，因此本环节可以直接跳过。

需要注意的是，一般来说围绕原始特征的特征筛选工作都会一定程度放宽要求，除非是非常肯定的无用特征，否则一般都会考虑保留，以最大程度保留衍生特征的可能性原始数据集的完整信息（当然，原始数据集特征非常多的情况除外）。而如果是衍生特征，则可以根据实际情况提高筛选门槛，以提高后续模型筛选和训练的效率。

• 时序衍生特征

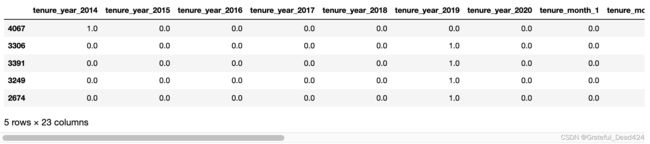
  由于本数据时序特征较为特殊，在此前的数据准备过程中已经手动完成了相关特征的衍生工作：

X_train_seq.head()

X_train_seq.shape
#(5282, 23)

时序衍生均为离散特征，考虑到后续将纳入这些特征进行交叉分组，因此创建一个包含所有离散特征变量名称的对象cat_all：

cat_all = (category_cols + list(X_train_seq.columns)).copy()
cat_all
# ['gender',
#  'SeniorCitizen',
#  'Partner',
#  'Dependents',
#  'PhoneService',
#  'MultipleLines',
#  'InternetService',
#  'OnlineSecurity',
#  'OnlineBackup',
#  'DeviceProtection',
#  'TechSupport',
#  'StreamingTV',
#  'StreamingMovies',
#  'Contract',
#  'PaperlessBilling',
#  'PaymentMethod',
#  'tenure_year_2014',
#  'tenure_year_2015',
#  'tenure_year_2016',
#  'tenure_year_2017',
#  'tenure_year_2018',
#  'tenure_year_2019',
#  'tenure_year_2020',
#  'tenure_month_1',
#  'tenure_month_2',
#  'tenure_month_3',
#  'tenure_month_4',
#  'tenure_month_5',
#  'tenure_month_6',
#  'tenure_month_7',
#  'tenure_month_8',
#  'tenure_month_9',
#  'tenure_month_10',
#  'tenure_month_11',
#  'tenure_month_12',
#  'tenure_quarter_1',
#  'tenure_quarter_2',
#  'tenure_quarter_3',
#  'tenure_quarter_4']

• 写入本地

  为了方便后续单独调用某部分衍生特征，考虑将时序衍生特征写入本地：

X_train_seq.to_csv('featuresCreation/X_train_seq.csv', index=False)
X_test_seq.to_csv('featuresCreation/X_test_seq.csv', index=False)

二、交叉组合特征衍生与筛选

1.交叉组合特征衍生过程

  然后来进行交叉组合特征衍生。由于交叉组合并不会衍生太多特征，因此可以考虑带入包括时序特征在内的全部离散特征，并进行两两组合：

Cross_Combination?
#Signature: Cross_Combination(colNames, X_train, X_test, multi=False, OneHot=True)
#Docstring:
#交叉组合特征衍生函数
#
#:param colNames: 参与交叉衍生的列名称
#:param X_train: 训练集特征
#:param X_test: 测试集特征
#:param multi: 是否进行多变量交叉组合
#:param OneHot: 是否进行独热编码
#
#:return：交叉衍生后的新特征和特征名称
#File:      d:\work\jupyter\telco\features_creation.py
#Type:      function
# 调整index
X_train_seq.index = X_train.index
X_test_seq.index = X_test.index

# 拼接数据集
train_temp = pd.concat([X_train, X_train_seq], axis=1)
test_temp = pd.concat([X_test, X_test_seq], axis=1)

# 带有时序特征的交叉组合      
CrossComb_train, CrossComb_test, colNames_train_new, colNames_test_new = Cross_Combination(cat_all, 
                                                                                           train_temp, 
                                                                                           test_temp)
                                                                                           

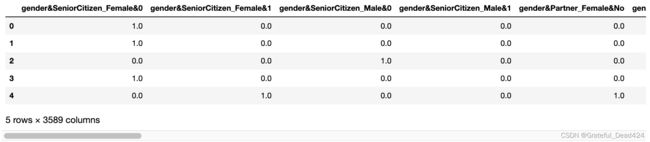
CrossComb_train.head()

CrossComb_train.shape
#(5282, 3589)

离散特征在两两组合情况下总共衍生3589个特征。

2.交叉组合特征筛选过程

• 方差过滤

  接下来，围绕交叉组合衍生特征进行特征筛选。这里首先可以考虑进行方差过滤。需要注意的是，交叉组合衍生的特征都是二分类离散变量，为了提高整体衍生特征质量，我们可以设置一个更高的方差阈值。这里考虑剔除少数类样本:多数类样本比例低于1:99的特征，即以0.01 * 0.99 = 0.0099为阈值，进行方差过滤：

0.01 * 0.99
#0.0099
from sklearn.feature_selection import VarianceThreshold
sel = VarianceThreshold()
sel.fit(CrossComb_train)
#VarianceThreshold()
CrossComb_cols = CrossComb_train.columns[sel.variances_ > 0.0099]
CrossComb_cols
# Index(['gender&SeniorCitizen_Female&0', 'gender&SeniorCitizen_Female&1',
#        'gender&SeniorCitizen_Male&0', 'gender&SeniorCitizen_Male&1',
#        'gender&Partner_Female&No', 'gender&Partner_Female&Yes',
#        'gender&Partner_Male&No', 'gender&Partner_Male&Yes',
#        'gender&Dependents_Female&No', 'gender&Dependents_Female&Yes',
#        ...
#        'tenure_quarter_1&tenure_quarter_4_1.0&0.0',
#        'tenure_quarter_2&tenure_quarter_3_0.0&0.0',
#        'tenure_quarter_2&tenure_quarter_3_0.0&1.0',
#        'tenure_quarter_2&tenure_quarter_3_1.0&0.0',
#        'tenure_quarter_2&tenure_quarter_4_0.0&0.0',
#        'tenure_quarter_2&tenure_quarter_4_0.0&1.0',
#        'tenure_quarter_2&tenure_quarter_4_1.0&0.0',
#        'tenure_quarter_3&tenure_quarter_4_0.0&0.0',
#        'tenure_quarter_3&tenure_quarter_4_0.0&1.0',
#        'tenure_quarter_3&tenure_quarter_4_1.0&0.0'],
#       dtype='object', length=3474)

能够发现，此处剔除了100多个特征。

• 卡方检验

  然后继续执行基于标签关联度的特征筛选。这里我们可以同时进行卡方检验和互信息法计算，然后选择两种方法挑选出来特征的交集（若希望选取更多衍生特征，也可以考虑二者的并集）。
  首先先进行卡方检验，并以0.01为阈值进行特征筛选：

from sklearn.feature_selection import chi2
CrossComb_train[CrossComb_cols].head()

chi2(CrossComb_train[CrossComb_cols], y_train)
#(array([4.70486948e+00, 5.34073272e+01, 1.26267171e+01, ...,
#        9.90547662e+01, 1.46860817e+02, 1.10886375e-03]),
# array([3.00772856e-02, 2.71083872e-13, 3.80272424e-04, ...,
#        2.45614672e-23, 8.41700181e-34, 9.73435668e-01]))
chi2_p = chi2(CrossComb_train[CrossComb_cols], y_train)[1]
chi2_CrossComb_cols = []

for pValue, colname in zip(chi2_p, CrossComb_cols):
    if pValue < 0.01:
        chi2_CrossComb_cols.append(colname)

print(len(chi2_CrossComb_cols))
#2495

最终挑选出2495个特征。

• 互信息法特征筛选

  接下来，继续进行互信息法的特征筛选：

from sklearn.feature_selection import mutual_info_classif
MI = mutual_info_classif(CrossComb_train[CrossComb_cols], y_train, discrete_features=True, random_state=22)
MI
#array([7.68870178e-04, 5.03288801e-03, 2.09448319e-03, ...,
#       1.80071779e-02, 1.94739071e-02, 1.34373500e-07])

  此处仍然可以采用众数量级后推小数点后两位的方法进行特征筛选，即设置0.1 * mean为阈值进行特征筛选：

MI.mean()
#0.010353000716212672
MI_threshold = MI.mean() * 0.1
MI_threshold
#0.0010353000716212671
MI_CrossComb_cols = []

for MIvalue, colname in zip(MI, CrossComb_cols):
    if MIvalue > MI_threshold:
        MI_CrossComb_cols.append(colname)

print(len(MI_CrossComb_cols))        
#2419

然后取方差分析和互信息法挑选出来特征的交集，可以通过如下方法实现：

set(chi2_CrossComb_cols) & set(MI_CrossComb_cols)

CrossComb_cols_select = list(set(chi2_CrossComb_cols) & set(MI_CrossComb_cols))
len(CrossComb_cols_select)
#2369

从最终结果能够看出，卡方检验和互信息法筛选出来的特征还是高度一致的，而CrossComb_cols_select也就是最终筛选出来的交叉组合衍生特征。

这里需要注意，由于上述过程涉及集合对象的创建，而集合是无序对象，因此最终输出的CrossComb_cols_select特征顺序会发生改变。

• 写入本地

  同样，我们将上述衍生特征写入本地：

CrossComb_train[CrossComb_cols_select]

CrossComb_train[CrossComb_cols_select].to_csv('featuresCreation/X_train_CrossComb.csv', index=False)
CrossComb_test[CrossComb_cols_select].to_csv('featuresCreation/X_test_CrossComb.csv', index=False)

三、多项式特征衍生与筛选

1.多项式特征衍生过程

  接下来进一步考虑多项式特征衍生。由于数据集只存在三个连续变量，可以考虑进行最高三阶多项式的、带入全部连续变量的两两组合多项式组合特征衍生：

Polynomial_Features?
# Signature: Polynomial_Features(colNames, degree, X_train, X_test, multi=False)
# Docstring:
# 多项式特征衍生函数

# :param colNames: 参与交叉衍生的列名称
# :param degree: 多项式最高阶
# :param X_train: 训练集特征
# :param X_test: 测试集特征
# :param multi: 是否进行多变量多项式组衍生

# :return：多项式衍生后的新特征和新列名称
# File:      d:\work\jupyter\telco\features_creation.py
# Type:      function
Poly_train, Poly_test, colNames_train_new, colNames_test_new = Polynomial_Features(numeric_cols, 
                                                                                   3, 
                                                                                   X_train, 
                                                                                   X_test, 
                                                                                   multi=False)

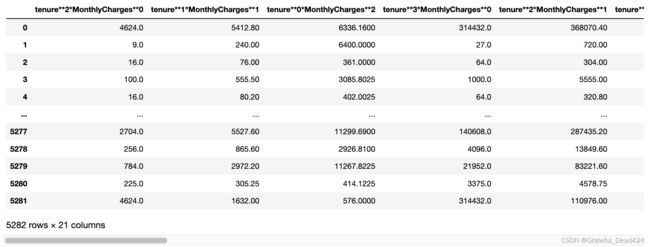
Poly_train.head()

Poly_train.shape
#(5282, 21)

多项式特征衍生总共创建21个新特征。

2.多项式衍生特征的特征筛选

• 方差过滤

  首先是方差过滤。多项式计算过程并不会造成大量零值，因此衍生特征中也不会存在方差为0的特征：

sel = VarianceThreshold()
sel.fit(Poly_train)
#VarianceThreshold()
Poly_cols = Poly_train.columns[sel.variances_ > 0]
Poly_cols = list(Poly_cols)
Poly_cols
# ['tenure**2*MonthlyCharges**0',
#  'tenure**1*MonthlyCharges**1',
#  'tenure**0*MonthlyCharges**2',
#  'tenure**3*MonthlyCharges**0',
#  'tenure**2*MonthlyCharges**1',
#  'tenure**1*MonthlyCharges**2',
#  'tenure**0*MonthlyCharges**3',
#  'tenure**2*TotalCharges**0',
#  'tenure**1*TotalCharges**1',
#  'tenure**0*TotalCharges**2',
#  'tenure**3*TotalCharges**0',
#  'tenure**2*TotalCharges**1',
#  'tenure**1*TotalCharges**2',
#  'tenure**0*TotalCharges**3',
#  'MonthlyCharges**2*TotalCharges**0',
#  'MonthlyCharges**1*TotalCharges**1',
#  'MonthlyCharges**0*TotalCharges**2',
#  'MonthlyCharges**3*TotalCharges**0',
#  'MonthlyCharges**2*TotalCharges**1',
#  'MonthlyCharges**1*TotalCharges**2',
#  'MonthlyCharges**0*TotalCharges**3']
len(Poly_cols)
#21

• 方差分析

  接下来继续进行基于关联度指标的特征筛选。多项式衍生特征都是连续变量，可以考虑方差分析和互信息计算，然后挑选二者选出特征的并集作为最终特征筛选结果。
  首先是方差分析特征筛选过程：

from sklearn.feature_selection import f_classif
f_classif(Poly_train, y_train)
# (array([613.06960446, 245.40152491, 124.76344154, 515.91186261,
#         292.16044487, 119.32037883,  78.31501911, 613.06960446,
#         291.00481002, 172.88676712, 515.91186261, 282.94514445,
#         181.83285997, 135.86888563, 124.76344154, 118.52840666,
#         172.88676712,  78.31501911,  79.18553416, 125.32427404,
#         135.86888563]),
#  array([3.82932349e-128, 4.24721102e-054, 1.19847172e-028, 4.75460035e-109,
#         8.52211388e-064, 1.75059872e-027, 1.17981151e-018, 3.82932349e-128,
#         1.47627483e-063, 7.03410902e-039, 4.75460035e-109, 6.83637464e-062,
#         9.06241025e-041, 5.09799183e-031, 1.19847172e-028, 2.58680629e-027,
#         7.03410902e-039, 1.17981151e-018, 7.64280682e-019, 9.09338472e-029,
#         5.09799183e-031]))
f_classif_p = f_classif(Poly_train, y_train)[1]
f_classif_Poly_cols = []

for pValue, colname in zip(f_classif_p, Poly_cols):
    if pValue < 0.01:
        f_classif_Poly_cols.append(colname)

print(len(f_classif_Poly_cols))
#21

  能够看出，多项式衍生的特征质量都比较高。

• 互信息法

  接下来继续执行互信息法的计算，由于全部衍生特征都是连续变量，因此在调用mutual_info_classif计算时不用进行额外参数设置：

MI = mutual_info_classif(Poly_train[Poly_cols], y_train)
MI
# array([0.08244379, 0.06146415, 0.04667433, 0.07714242, 0.07425349,
#        0.0271758 , 0.04536536, 0.0791969 , 0.04709366, 0.04340931,
#        0.07998568, 0.07682973, 0.0618343 , 0.04272974, 0.04856117,
#        0.04318058, 0.04326713, 0.04812398, 0.0258615 , 0.03179083,
#        0.04407073])

然后同样选取mean*0.1作为阈值进行特征筛选：

MI.mean()
#0.05383117009190194
MI_threshold = MI.mean() * 0.1
MI_threshold
#0.005383117009190194
MI_Ploy_cols = []

for MIvalue, colname in zip(MI, Poly_cols):
    if MIvalue > MI_threshold:
        MI_Ploy_cols.append(colname)

print(len(MI_Ploy_cols))    
#21

筛选结果仍然是保留全部21个衍生特征。因此，结合方差过滤、方差分析的结果，最终围绕多项式衍生的特征结果是保留全部特征：

Poly_cols_select = Poly_cols
Poly_cols_select
# ['tenure**2*MonthlyCharges**0',
#  'tenure**1*MonthlyCharges**1',
#  'tenure**0*MonthlyCharges**2',
#  'tenure**3*MonthlyCharges**0',
#  'tenure**2*MonthlyCharges**1',
#  'tenure**1*MonthlyCharges**2',
#  'tenure**0*MonthlyCharges**3',
#  'tenure**2*TotalCharges**0',
#  'tenure**1*TotalCharges**1',
#  'tenure**0*TotalCharges**2',
#  'tenure**3*TotalCharges**0',
#  'tenure**2*TotalCharges**1',
#  'tenure**1*TotalCharges**2',
#  'tenure**0*TotalCharges**3',
#  'MonthlyCharges**2*TotalCharges**0',
#  'MonthlyCharges**1*TotalCharges**1',
#  'MonthlyCharges**0*TotalCharges**2',
#  'MonthlyCharges**3*TotalCharges**0',
#  'MonthlyCharges**2*TotalCharges**1',
#  'MonthlyCharges**1*TotalCharges**2',
#  'MonthlyCharges**0*TotalCharges**3']

• 写入本地

  同样，我们将上述衍生特征写入本地：

Poly_train[Poly_cols_select]

Poly_train[Poly_cols_select].to_csv('featuresCreation/X_train_Poly.csv', index=False)
Poly_test[Poly_cols_select].to_csv('featuresCreation/X_test_Poly.csv', index=False)

四、分组统计特征衍生与筛选

1.分组统计特征衍生

  接下来进行分组统计特征衍生，此处若如果带入全部离散特征进行带拓展项的分组统计特征衍生，则会创建近10万条特征。考虑到数据集本身样本数量只有五千多条，我们可以考虑借助此前探索得到的“分组衍生特征性能和KeyCol原始性能接近”的规律，提前对KeyCol进行筛选，只挑选那些表现较好的KeyCol进行分组统计特征衍生，以提高整体执行效率。

• KeyCol筛选

  这里围绕cat_all离散变量的筛选可以用卡方检验也可以用互信息法，这里我们采用一种组合方法，即先用卡方检验剔除显著性不到0.01的特征，再用互信息法剔除那些MI值明显小于众数的特征，然后最终取交集。具体执行流程如下：

# 拼接数据集
train_temp_OE = pd.concat([X_train_OE, X_train_seq], axis=1)
test_temp_OE = pd.concat([X_test_OE, X_test_seq], axis=1)
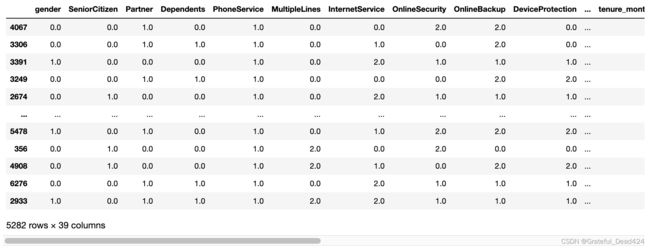
train_temp_OE[cat_all]

y_train
# 4067    0
# 3306    0
# 3391    0
# 3249    0
# 2674    0
#        ..
# 5478    0
# 356     0
# 4908    1
# 6276    0
# 2933    0
# Name: Churn, Length: 5282, dtype: int64
chi2(train_temp_OE[cat_all], y_train)
#(array([9.11414942e-01, 8.73653155e+01, 6.99267855e+01, 8.58416151e+01,
#        3.28337137e-03, 5.05565036e+00, 9.87028913e+00, 4.70600801e+02,
#        1.79111384e+02, 1.66587107e+02, 4.13243802e+02, 6.73755161e+00,
#        1.06279915e+01, 8.30862655e+02, 7.51550195e+01, 5.15568690e+01,
#        2.18414361e+02, 4.71022384e+01, 2.04721265e+01, 6.82195893e+00,
#        2.93245371e+00, 3.73933423e+02, 3.54011792e+00, 8.08923275e+01,
#        3.28456745e+01, 1.81976499e+00, 6.08334094e+00, 1.10199338e+01,
#        1.68886049e+00, 1.83342748e+00, 3.25740687e-02, 1.42652376e+00,
#        6.54213677e+00, 1.15481920e+01, 1.74805428e+02, 9.35057147e+01,
#        1.66365418e+01, 1.10886375e-03, 1.46860817e+02]),
# array([3.39739272e-001, 9.02188129e-021, 6.15469914e-017, 1.94940242e-020,
#        9.54305655e-001, 2.45457682e-002, 1.67969111e-003, 2.37153824e-104,
#        7.57606574e-041, 4.11736822e-038, 7.21175221e-092, 9.44041024e-003,
#        1.11388631e-003, 1.05225513e-182, 4.35169013e-018, 6.95529154e-013,
#        2.00566021e-049, 6.73786928e-012, 6.05060006e-006, 9.00437475e-003,
#        8.68154542e-002, 2.60482189e-083, 5.99012025e-002, 2.38357316e-019,
#        9.97728284e-009, 1.77341253e-001, 1.36462456e-002, 9.01372909e-004,
#        1.93751250e-001, 1.75723244e-001, 8.56773496e-001, 2.32332602e-001,
#        1.05348739e-002, 6.78151694e-004, 6.60231742e-040, 4.05029391e-022,
#        4.52703733e-005, 9.73435668e-001, 8.41700181e-034]))
chi2_p = chi2(train_temp_OE[cat_all], y_train)[1]
chi2_select_cols = []

for pValue, colname in zip(chi2_p, cat_all):
    if pValue < 0.01:
        chi2_select_cols.append(colname)

print(len(chi2_select_cols))
chi2_select_cols
# 26
# ['SeniorCitizen',
#  'Partner',
#  'Dependents',
#  'InternetService',
#  'OnlineSecurity',
#  'OnlineBackup',
#  'DeviceProtection',
#  'TechSupport',
#  'StreamingTV',
#  'StreamingMovies',
#  'Contract',
#  'PaperlessBilling',
#  'PaymentMethod',
#  'tenure_year_2014',
#  'tenure_year_2015',
#  'tenure_year_2016',
#  'tenure_year_2017',
#  'tenure_year_2019',
#  'tenure_month_1',
#  'tenure_month_2',
#  'tenure_month_5',
#  'tenure_month_11',
#  'tenure_month_12',
#  'tenure_quarter_1',
#  'tenure_quarter_2',
#  'tenure_quarter_4']

  接下来继续执行互信息法特征筛选：

MI = mutual_info_classif(train_temp_OE[cat_all], y_train, discrete_features=True, random_state=22)
MI
# array([1.73090078e-04, 9.13473736e-03, 1.29159500e-02, 1.24089586e-02,
#        3.11949909e-06, 4.99279481e-04, 5.43286385e-02, 7.08580232e-02,
#        4.78061879e-02, 4.70107520e-02, 6.57416875e-02, 3.30813850e-02,
#        3.34860937e-02, 9.78731272e-02, 1.81578691e-02, 4.59939447e-02,
#        3.20973276e-02, 5.65419301e-03, 2.33501821e-03, 7.58878530e-04,
#        3.18699916e-04, 4.89210895e-02, 5.74417822e-04, 1.02552592e-02,
#        3.81369383e-03, 1.90633022e-04, 6.48159371e-04, 1.19899259e-03,
#        1.76110815e-04, 1.91702192e-04, 3.30476176e-06, 1.43599947e-04,
#        6.48822228e-04, 1.14373671e-03, 1.75928217e-02, 1.30391564e-02,
#        2.05498995e-03, 1.34373500e-07, 1.94739071e-02])

此处仍然可以采用均值*0.1作为阈值进行特征筛选：

MI_select_cols = []
MI_threshold = MI.mean() * 0.1

for MIvalue, colname in zip(MI, cat_all):
    if MIvalue > MI_threshold:
        MI_select_cols.append(colname)

print(len(MI_select_cols))        
MI_select_cols
# 23
# ['SeniorCitizen',
#  'Partner',
#  'Dependents',
#  'InternetService',
#  'OnlineSecurity',
#  'OnlineBackup',
#  'DeviceProtection',
#  'TechSupport',
#  'StreamingTV',
#  'StreamingMovies',
#  'Contract',
#  'PaperlessBilling',
#  'PaymentMethod',
#  'tenure_year_2014',
#  'tenure_year_2015',
#  'tenure_year_2016',
#  'tenure_year_2019',
#  'tenure_month_1',
#  'tenure_month_2',
#  'tenure_month_12',
#  'tenure_quarter_1',
#  'tenure_quarter_2',
#  'tenure_quarter_4']

然后取方差分析和互信息法挑选出来特征的交集：

set(chi2_select_cols) & set(MI_select_cols)
# {'Contract',
#  'Dependents',
#  'DeviceProtection',
#  'InternetService',
#  'OnlineBackup',
#  'OnlineSecurity',
#  'PaperlessBilling',
#  'Partner',
#  'PaymentMethod',
#  'SeniorCitizen',
#  'StreamingMovies',
#  'StreamingTV',
#  'TechSupport',
#  'tenure_month_1',
#  'tenure_month_12',
#  'tenure_month_2',
#  'tenure_quarter_1',
#  'tenure_quarter_2',
#  'tenure_quarter_4',
#  'tenure_year_2014',
#  'tenure_year_2015',
#  'tenure_year_2016',
#  'tenure_year_2019'}

接下来我们采用这些特征作为KeyCol来进行分组统计特征衍生：

# 创建一个未被选中离散变量的list
cat_rest = []

for col in cat_all:
    if col not in keycol:
        cat_rest.append(col)

cat_rest
# ['gender',
#  'PhoneService',
#  'MultipleLines',
#  'tenure_year_2017',
#  'tenure_year_2018',
#  'tenure_year_2020',
#  'tenure_month_3',
#  'tenure_month_4',
#  'tenure_month_5',
#  'tenure_month_6',
#  'tenure_month_7',
#  'tenure_month_8',
#  'tenure_month_9',
#  'tenure_month_10',
#  'tenure_month_11',
#  'tenure_quarter_3']

• 分组统计特征衍生

Group_Statistics?
# 创建容器
col_temp = keycol.copy()
GroupStat_train = pd.DataFrame()
GroupStat_test = pd.DataFrame()

for i in range(len(col_temp)):
    keyCol = col_temp.pop(i)
    features_train1, features_test1, colNames_train, colNames_test = Group_Statistics(keyCol,
                                                                                      train_temp_OE,
                                                                                      test_temp_OE,
                                                                                      col_num=numeric_cols,
                                                                                      col_cat=col_temp+cat_rest, 
                                                                                      extension=True)
    
    GroupStat_train = pd.concat([GroupStat_train, features_train1],axis=1)
    GroupStat_test = pd.concat([GroupStat_test, features_test1],axis=1)
    
    col_temp = keycol.copy()
    
GroupStat_train.head()

GroupStat_train.shape
#(5282, 16905)

分组统计特征衍生最终创建了16905个特征。

2.分组统计衍生特征的特征筛选

• 分组统计特征变量类型讨论

  接下来，考虑围绕分组统计衍生特征进行特征筛选。这里需要注意，分组统计衍生特征从原理层面来看应该属于离散变量，这些特征取值大小本身不仅具有标记作用，而且具有数值绝对大小意义（都是统计量的计算结果）。但同时，这些特征的数值分布和KeyCol一致，也就是尽管是连续变量，但取值个数有限。例如衍生特征’tenure_month_10_DeviceProtection_mean’，是tenure_month_10在DeviceProtection分组下组内均值计算结果，均值本身数值有数值大小意义，数值越小代表组内用户10月入网占比越少，但同时tenure_month_10_DeviceProtection_mean只有三个不同的取值，且分布和DeviceProtection数值分布相同：

GroupStat_train['tenure_month_10_DeviceProtection_mean']
# 0       0.088851
# 1       0.088851
# 2       0.080142
# 3       0.069307
# 4       0.080142
#           ...   
# 5277    0.069307
# 5278    0.088851
# 5279    0.069307
# 5280    0.080142
# 5281    0.080142
# Name: tenure_month_10_DeviceProtection_mean, Length: 5282, dtype: float64
GroupStat_train['tenure_month_10_DeviceProtection_mean'].nunique()
#3
X_train_OE['DeviceProtection']
#4067    0.0
#3306    0.0
#3391    1.0
#3249    2.0
#2674    1.0
#       ... 
#5478    2.0
#356     0.0
#4908    2.0
#6276    1.0
#2933    1.0
#Name: DeviceProtection, Length: 5282, dtype: float64
X_train_OE['DeviceProtection'].nunique()
#3

同时我们也能够观察到，很多时候由于被分组统计的都是0-1离散变量，因此不同组的部分统计量（如均值）的统计结果也都是在0-1之间，并且彼此差异并不大。

• 方差过滤

  基于分组统计衍生特征的基本情况，我们可以制定如下特征筛选策略：首先，无需进行缺失值过滤，由于我们自定义的特征衍生函数并不会创造缺失值，而原始数据集中的缺失值已经完成了填补，因此无需进行缺失值过滤；其次，对于方差过滤来说，零方差过滤是必须要执行的，但小方差过滤意义不大，即只剔除那些零方差的特征，而不剔除小方差的特征。这么做的主要原因是很多统计结果数值都较小，并且同一列的不同取值差异并不大，如上述tenure_month_10_DeviceProtection_mean，而这些特征数值较小的根本原因因为被统计的离散变量数值较小，即tenure_month_10_DeviceProtection_mean特征取值较小的原因是tenure_month_10是0-1变量，而如果把0、1这两个数值标记改为0、100（tenure_month_10是名义变量，数值没有大小意义，可以任意修改数值标记），则衍生特征tenure_month_10_DeviceProtection_mean取值也会变大。但这种数值上的变化没有任何意义，因此从这个角度来说，无需对分组统计特征进行小方差特征过滤。
  接下来对分组统计衍生特征进行0方差过滤：

sel = VarianceThreshold()
sel.fit(GroupStat_train)
#VarianceThreshold()
GroupStat_cols = list(GroupStat_train.columns[sel.variances_ > 0])
len(GroupStat_cols)
#11345

能够看出，0方差过滤还是剔除了很多特征的，最终剩下11345个特征。这里我们可以进一步观察0方差过滤到底剔除了那些特征：

set(GroupStat_train.columns) - set(GroupStat_cols)

GroupStat_train['tenure_quarter_4_PaperlessBilling_median']
#0       0.0
#1       0.0
#2       0.0
#3       0.0
#4       0.0
#       ... 
#5277    0.0
#5278    0.0
#5279    0.0
#5280    0.0
#5281    0.0
#Name: tenure_quarter_4_PaperlessBilling_median, Length: 5282, dtype: float64
GroupStat_train['InternetService_PaymentMethod_max']
# 0       2.0
# 1       2.0
# 2       2.0
# 3       2.0
# 4       2.0
#        ... 
# 5277    2.0
# 5278    2.0
# 5279    2.0
# 5280    2.0
# 5281    2.0
# Name: InternetService_PaymentMethod_max, Length: 5282, dtype: float64

能够看出，大多数剔除的特征都是统计变量为离散变量时进行的数值分布规律的统计量，例如极值、四分位数等。仔细思考其实也不难理解，很多时候不同组内的离散变量取值分布较为类似，例如不同支付方式的用户都有没有购买互联网服务的情况，此时就会出现’InternetService_PaymentMethod_max’全都取值为2的情况。因此围绕分组统计衍生特征进行0方差的过滤是非常有必要的。

但这里需要注意，尽管很多离散变量不同组的极值、分位数的分组统计结果相同，但这并不代表极值、分位数等统计量不重要。恰好相反的是，正是因为很多离散变量的不同组的极值、分位数的分组统计结果相同，那些不同组内极值、分位数的分组统计结果不同的特征，往往是提升模型效果的关键。

而GroupStat_cols就是经过方差过滤后的特征名称列表。

• 方差分析

  接下来继续考虑进行标签关联度指标特征筛选。正如此前所说，分组统计的特征本质上其实是连续变量，因此可以考虑方差分析与互信息法特征筛选。并且根据之前介绍的方差分析与互信息的基本原理可知，两种方法并不会受连续变量的绝对数值大小影响，因此可信度较高。
  首先是方差分析，我们带入全部方差过滤后的GroupStat_cols进行检验：

f_classif_p = f_classif(GroupStat_train[GroupStat_cols], y_train)[1]

f_classif_GroupStat_cols = []

for pValue, colname in zip(f_classif_p, GroupStat_cols):
    if pValue < 0.01:
        f_classif_GroupStat_cols.append(colname)

print(len(f_classif_GroupStat_cols))
#11123

• 互信息法

  接下来继续执行互信息法的计算，由于全部衍生特征都是连续变量，因此在调用mutual_info_classif计算时不用进行额外参数设置：

MI = mutual_info_classif(GroupStat_train[GroupStat_cols], y_train, random_state=22)
MI
#array([0.00454814, 0.        , 0.0120663 , ..., 0.03797375, 0.02559527,
#       0.02455003])

然后同样选取mean*0.1作为阈值进行特征筛选：

MI.mean()
#0.03027058891310412
MI_threshold = MI.mean() * 0.1
MI_threshold
#0.003027058891310412
MI_GroupStat_cols = []

for MIvalue, colname in zip(MI, GroupStat_cols):
    if MIvalue > MI_threshold:
        MI_GroupStat_cols.append(colname)

print(len(MI_GroupStat_cols))  
#10210

最后将两种方法挑选出来的特征取交集，并得到最终筛选出来的特征GroupStat_cols_select：

GroupStat_cols_select = list(set(f_classif_GroupStat_cols) & set(MI_GroupStat_cols))
len(GroupStat_cols_select)
#9988

总共有9988个特征，在整个初筛阶段，总共剔除了40%个衍生特征：

1 - 9988/16905
#0.4091688849452825

需要注意的是，尽管我们在互信息法中设置了随机数种子，但由于本身数值精度较高，因此会在小数点后6位左右存在误差，这也会导致筛选结果会存在随机性。

• 写入本地

  同样，我们将上述衍生特征写入本地：

GroupStat_train[GroupStat_cols_select]

GroupStat_train[GroupStat_cols_select].to_csv('featuresCreation/X_train_GroupStat.csv', index=False)
GroupStat_test[GroupStat_cols_select].to_csv('featuresCreation/X_test_GroupStat.csv', index=False)

五、目标编码特征衍生与筛选

1.目标编码特征衍生过程

  接下来继续进行目标编码，由于目标编码本身的计算特性，较强的KeyCol不一定能衍生出较强的特征，因此需要带入全部离散特征进行计算。此外，由于目标编码的特殊性，有效特征产出率较低，因此建议采用extension方式进行特征衍生，创建更多特征：

Target_Encode?

# 定义标签
col_cat = [target]
print(col_cat)

# 创建容器
col_temp = cat_all.copy()
TarEnc_train = pd.DataFrame()
TarEnc_test = pd.DataFrame()

for keyCol in col_temp:
    features_train1, features_test1, colNames_train_new, colNames_test_new = Target_Encode(keyCol, 
                                                                                           train_temp_OE, 
                                                                                           y_train,
                                                                                           test_temp_OE, 
                                                                                           col_cat=col_cat, 
                                                                                           extension=True)
    
    TarEnc_train = pd.concat([TarEnc_train, features_train1],axis=1)
    TarEnc_test = pd.concat([TarEnc_test, features_test1],axis=1)
    
    col_temp = cat_all.copy()
#['Churn']
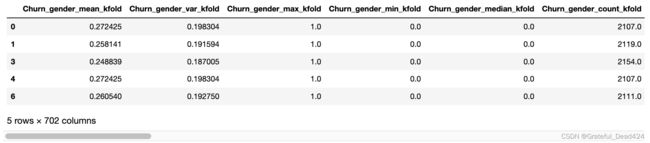
TarEnc_train.head()

TarEnc_train.shape
#(5282, 702)

2.目标编码特征筛选

  接下来继续进行目标编码的衍生特征的特征筛选。目标编码也是某种意义上的分组统计，因此首先需要进行零值方差过滤，然后再考虑使用标签关联度指标进行特征筛选。

• 方差过滤

  首先是方差过滤，这里仍然采用0值方差过滤：

sel = VarianceThreshold()
sel.fit(TarEnc_train)
#VarianceThreshold()
TarEnc_cols = list(TarEnc_train.columns[sel.variances_ > 0])
len(TarEnc_cols)
#456

能够看出，在0方差过滤中被剔除的特征也大都是组内分布统计量：

set(TarEnc_train.columns) - set(TarEnc_cols)

TarEnc_train['Churn_Contract_max_kfold']
# 0       1.0
# 1       1.0
# 3       1.0
# 4       1.0
# 6       1.0
#        ... 
# 7038    1.0
# 7039    1.0
# 7040    1.0
# 7041    1.0
# 7042    1.0
# Name: Churn_Contract_max_kfold, Length: 5282, dtype: float64

• 方差分析

  接下来进行目标编码的标签关联度特征筛选，这里需要注意的是目标编码衍生出来的特征都是间接统计出来的结果，因此从数值层面上来看，衍生特征和标签的关联度或者和标签分布的一致性都会比较若，但这并不代表这些特征在建模过程中无法提供有效信息。简而言之，目标编码的衍生特征往往在标签关联度指标上会表现较弱（这点在特征衍生的实验中也有所体现），因此在进行特征筛选时可以略微放宽条件。

换个角度来说，之所以要进行交叉统计，也是为了让衍生特征的分布和标签分布尽可能有差异，以免标签信息泄露。

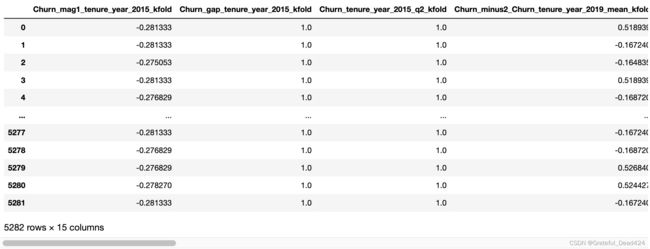
f_classif_p = f_classif(TarEnc_train[TarEnc_cols], y_train)[1]
f_classif_p

能够大概看出，整体p值较高，因此这里在进行特征筛选时，可以稍微放宽显著性水平，由原来的0.01改为0.05。筛选过程如下：

f_classif_TarEnc_cols = []

for pValue, colname in zip(f_classif_p, TarEnc_cols):
    if pValue < 0.05:
        f_classif_TarEnc_cols.append(colname)

print(len(f_classif_TarEnc_cols))
#28
f_classif_TarEnc_cols
# ['Churn_cv_OnlineBackup_kfold',
#  'Churn_PaymentMethod_q2_kfold',
#  'Churn_dive1_Churn_PaymentMethod_mean_kfold',
#  'Churn_gap_PaymentMethod_kfold',
#  'Churn_tenure_year_2015_mean_kfold',
#  'Churn_tenure_year_2015_var_kfold',
#  'Churn_tenure_year_2015_count_kfold',
#  'Churn_tenure_year_2015_q2_kfold',
#  'Churn_dive1_Churn_tenure_year_2015_mean_kfold',
#  'Churn_dive2_Churn_tenure_year_2015_median_kfold',
#  'Churn_minus1_Churn_tenure_year_2015_mean_kfold',
#  'Churn_minus2_Churn_tenure_year_2015_mean_kfold',
#  'Churn_norm_tenure_year_2015_kfold',
#  'Churn_gap_tenure_year_2015_kfold',
#  'Churn_mag1_tenure_year_2015_kfold',
#  'Churn_cv_tenure_year_2015_kfold',
#  'Churn_tenure_year_2019_mean_kfold',
#  'Churn_tenure_year_2019_var_kfold',
#  'Churn_tenure_year_2019_count_kfold',
#  'Churn_tenure_year_2019_q2_kfold',
#  'Churn_dive1_Churn_tenure_year_2019_mean_kfold',
#  'Churn_dive2_Churn_tenure_year_2019_median_kfold',
#  'Churn_minus1_Churn_tenure_year_2019_mean_kfold',
#  'Churn_minus2_Churn_tenure_year_2019_mean_kfold',
#  'Churn_norm_tenure_year_2019_kfold',
#  'Churn_gap_tenure_year_2019_kfold',
#  'Churn_mag1_tenure_year_2019_kfold',
#  'Churn_cv_tenure_year_2019_kfold']

最终筛选出28个特征。

• 互信息法

  接下来继续进行互信息法的特征筛选。这里有两点需要注意，其一是因为目标编码衍生的特征和标签关联度较弱，因此互信息计算结果整体数值较小，建议加上随机数种子以确保结果可以重复。其二则是这里也可以考虑放宽筛选条件，但由于互信息的筛选阈值是基于均值制定的，无论是否放宽筛选条件，互信息的阈值总是能一定程度确保最后筛选出来的特征数量（严重左偏除外）的，在方差分析仅筛选出了28个特征并且最终取交集的情况下，互信息无论是否放宽筛选条件，对最终的结果都不一定会有太大影响。

MI = mutual_info_classif(TarEnc_train[TarEnc_cols], y_train, random_state=22)
len(MI)
#456

然后同样选取mean*0.01作为阈值进行特征筛选：

MI.mean()
#0.0025913521951452675
MI_threshold = MI.mean() * 0.01
MI_threshold
#2.5913521951452675e-05
MI_TarEnc_cols = []

for MIvalue, colname in zip(MI, TarEnc_cols):
    if MIvalue > MI_threshold:
        MI_TarEnc_cols.append(colname)

print(len(MI_TarEnc_cols))  
#232

最后将两种方法挑选出来的特征取交集，并得到最终筛选出来的特征TarEnc_cols_select：

TarEnc_cols_select = list(set(f_classif_TarEnc_cols) & set(MI_TarEnc_cols))
len(TarEnc_cols_select)
#15
TarEnc_cols_select
# ['Churn_mag1_tenure_year_2015_kfold',
#  'Churn_gap_tenure_year_2015_kfold',
#  'Churn_tenure_year_2015_q2_kfold',
#  'Churn_minus2_Churn_tenure_year_2019_mean_kfold',
#  'Churn_norm_tenure_year_2019_kfold',
#  'Churn_tenure_year_2019_q2_kfold',
#  'Churn_dive1_Churn_PaymentMethod_mean_kfold',
#  'Churn_norm_tenure_year_2015_kfold',
#  'Churn_cv_OnlineBackup_kfold',
#  'Churn_tenure_year_2015_count_kfold',
#  'Churn_minus2_Churn_tenure_year_2015_mean_kfold',
#  'Churn_tenure_year_2015_var_kfold',
#  'Churn_PaymentMethod_q2_kfold',
#  'Churn_tenure_year_2019_mean_kfold',
#  'Churn_dive2_Churn_tenure_year_2019_median_kfold']

• 写入本地

  同样，我们将上述衍生特征写入本地：

TarEnc_train[TarEnc_cols_select].reset_index(drop=True)

TarEnc_train[TarEnc_cols_select].reset_index(drop=True).to_csv('featuresCreation/X_train_TarEnc.csv', index=False)
TarEnc_test[TarEnc_cols_select].reset_index(drop=True).to_csv('featuresCreation/X_test_TarEnc.csv', index=False)

六、NLP特征衍生与筛选

  NLP特征衍生无论是特征衍生过程还是特征筛选过程，都基本上和分组统计特征过程类似，衍生过程需要采用更强的KeyCol以增强特征衍生效果，而筛选过程则是将衍生特征视作连续变量，采用0值方差过滤、方差分析以及互信息法进行特征筛选。

1.NLP特征衍生过程

  NLP特征衍生分为两部分执行，首先是围绕较强原始特征的IT-IDF特征衍生，然后是以这些较强原始特征为KeyCol来进行分组CountVectorizer和IT-IDF计算：

NLP_Group_Stat?
# 关键变量
col_temp = keycol.copy()

# 单变量if-idf计算
NLP_train, NLP_test, colNames_train_new, colNames_test_new = NLP_Group_Stat(train_temp_OE, 
                                                                            test_temp_OE, 
                                                                            col_temp)

# 以强原始特征作为keycol进行分组NLP特征衍生
for i in range(len(col_temp)):
    keyCol = col_temp.pop(i)
    features_train1, features_test1, colNames_train, colNames_test = NLP_Group_Stat(train_temp_OE, 
                                                                                    test_temp_OE, 
                                                                                    col_temp+cat_rest,
                                                                                    keyCol)
    
    NLP_train = pd.concat([NLP_train, features_train1],axis=1)
    NLP_test = pd.concat([NLP_test, features_test1],axis=1)
    
    col_temp = keycol.copy()

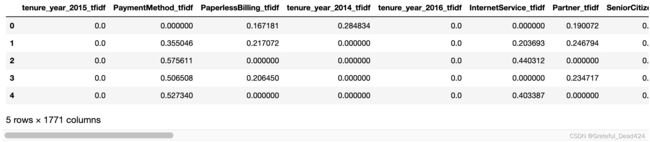
NLP_train.head()

NLP_train.shape
#(5282, 1771)

NLP特征衍生总共创建1771个特征。

2.NLP衍生特征的筛选过程

  接下来继续进行特征筛选，同样也是方差过滤、方差分析和互信息法三部分：

• 方差过滤

  首先是方差过滤，这里仍然采用0值方差过滤：

sel = VarianceThreshold()
sel.fit(NLP_train)
#VarianceThreshold()
NLP_cols = list(NLP_train.columns[sel.variances_ > 0])
len(NLP_cols)
#1771

  能够看出，NLP衍生特征中并不存在0方差的特征，主要原因也是组内元素个数的统计和TF-IDF的计算不太可能出现完全相同的结果。

• 方差分析

  然后进一步进行方差分析：

f_classif_p = f_classif(NLP_train[NLP_cols], y_train)[1]
f_classif_p
#array([4.53400235e-12, 4.44310685e-47, 8.16284694e-77, ...,
#       3.18557233e-20, 1.74233920e-27, 1.79119043e-52])

这里仍然选取0.01为阈值，进行特征筛选：

f_classif_NLP_cols = []

for pValue, colname in zip(f_classif_p, NLP_cols):
    if pValue < 0.01:
        f_classif_NLP_cols.append(colname)

print(len(f_classif_NLP_cols))
#1744

最终筛选出1744个特征，大部分特征都经过了方差分析的筛选。

• 互信息法

  接下来进行互信息法特征筛选：

MI = mutual_info_classif(NLP_train[NLP_cols], y_train, random_state=22)
MI
#array([0.01609048, 0.06766434, 0.07854761, ..., 0.03468068, 0.03966413,
#       0.02046427])
len(MI)
#1771

然后同样选取mean*0.1作为阈值进行特征筛选：

MI.mean()
#0.031270008838771964
MI_threshold = MI.mean() * 0.1
MI_threshold
#0.0031270008838771967
MI_NLP_cols = []

for MIvalue, colname in zip(MI, NLP_cols):
    if MIvalue > MI_threshold:
        MI_NLP_cols.append(colname)

print(len(MI_NLP_cols))    
#1603

互信息法挑选出1603个特征。最后将两种方法挑选出来的特征取交集，并得到最终筛选出来的特征NLP_cols_select：

NLP_cols_select = list(set(f_classif_NLP_cols) & set(MI_NLP_cols))
len(NLP_cols_select)
#1576

最终筛选出1576个特征。而至此，我们也完成了全部特征衍生及初步特征筛选工作。

• 写入本地

  同样，我们将上述衍生特征写入本地：

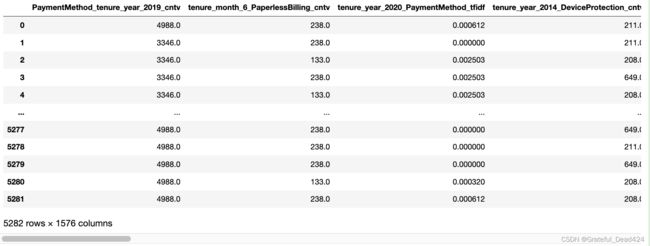
NLP_train[NLP_cols_select]

NLP_train[NLP_cols_select].to_csv('featuresCreation/X_train_NLP.csv', index=False)
NLP_test[NLP_cols_select].to_csv('featuresCreation/X_test_NLP.csv', index=False)

七、关于平衡效率与效果的相关讨论

  需要注意的是，关于上述特征衍生与特征筛选的流程，并不是完全固定的，也并不一定是唯一最优的策略，总体来看仍然是希望能够在保证效率的情况下，尽可能创建更好的结果，也就是做到效果和效率的平衡。

• 上行拓展

  当然，如果算力足够，也可以在每个阶段进行更大规模的特征衍生，如多变量交叉组合、三阶多项式、双变量交叉组合分组衍生等等，同时也完全可以在特征初筛阶段放宽筛选要求，例如都以p值0.05作为阈值进行筛选、或者选择互信息的均值作为阈值进行筛选等。当然，这样一来，特征筛选的压力就会转移到下个阶段、也就是带入模型进行特征筛选的阶段。这样一来或许能创建更多更好的特征，但也将极大的增加算力的消耗。

• 下行拓展

  另一方面，如果算力紧张，也可以略微精简上述流程，例如只针对效果最好的连续变量进行多项式衍生、提高分组统计特征衍生KeyCol的筛选标准等等；而在特征筛选阶段，也可以稍微提高特征筛选阈值，以减少下个阶段模型筛选的算力压力。当然，代价就是可能会损失一些对建模有帮助的高价值特征。
  不过就目前数据集的数据量规模来看，当前的特征衍生和特征筛选流程是能够较好的兼顾到效果和效率。上述全部代码运行耗时差不多在10分钟内，没有必要再精简流程。

八、衍生特征读取过程

  如果是从本部分开始运行代码，则可以通过如下过程进行衍生特征读取与全数据拼接。

• 衍生特征读取

X_train_seq = pd.read_csv('featuresCreation/X_train_seq.csv')
X_train_CrossComb = pd.read_csv('featuresCreation/X_train_CrossComb.csv')
X_train_Poly = pd.read_csv('featuresCreation/X_train_Poly.csv')
X_train_GroupStat = pd.read_csv('featuresCreation/X_train_GroupStat.csv')
X_train_TarEnc = pd.read_csv('featuresCreation/X_train_TarEnc.csv')
X_train_NLP = pd.read_csv('featuresCreation/X_train_NLP.csv')
X_test_seq = pd.read_csv('featuresCreation/X_test_seq.csv')
X_test_CrossComb = pd.read_csv('featuresCreation/X_test_CrossComb.csv')
X_test_Poly = pd.read_csv('featuresCreation/X_test_Poly.csv')
X_test_GroupStat = pd.read_csv('featuresCreation/X_test_GroupStat.csv')
X_test_TarEnc = pd.read_csv('featuresCreation/X_test_TarEnc.csv')
X_test_NLP = pd.read_csv('featuresCreation/X_test_NLP.csv')

• 数据集拼接

features_train_new = pd.concat([X_train_seq, 
                                X_train_CrossComb, 
                                X_train_Poly, 
                                X_train_GroupStat, 
                                X_train_TarEnc, 
                                X_train_NLP], axis=1)
features_test_new = pd.concat([X_test_seq, 
                               X_test_CrossComb, 
                               X_test_Poly, 
                               X_test_GroupStat, 
                               X_test_TarEnc, 
                               X_test_NLP], axis=1)
features_train_new.shape
#(5282, 13992)
features_test_new.shape
#(1761, 13992)
assert features_train_new.shape[1] == (X_train_seq.shape[1] + 
                                       X_train_CrossComb.shape[1] + 
                                       X_train_Poly.shape[1] + 
                                       X_train_GroupStat.shape[1] + 
                                       X_train_TarEnc.shape[1] + 
                                       X_train_NLP.shape[1])
assert features_test_new.shape[1] == (X_test_seq.shape[1] + 
                                      X_test_CrossComb.shape[1] + 
                                      X_test_Poly.shape[1] + 
                                      X_test_GroupStat.shape[1] + 
                                      X_test_TarEnc.shape[1] + 
                                      X_test_NLP.shape[1])
features_train_new.head()

• 写入完整的衍生特征数据集

features_train_new.to_csv('featuresCreation/features_train_new.csv', index=False)
features_test_new.to_csv('featuresCreation/features_test_new.csv', index=False)

后续的各项建模工作将统一上述数据集作为衍生数据集。