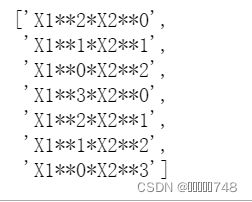特征工程衍生技术

视频入口：【完整合集】机器学习特征衍生全方法精讲|特征工程|机器学习竞赛提分|机器学习模型优化_哔哩哔哩_bilibili

 

特征衍生的介绍

本质

对既有数据信息的重新排布。

需要知道的是，特征衍生本身不是去创造更多信息，而是借助现有的数据去组合出一些新的数据，进而提高建模效果。

过程

简单的围绕单个列进行变换或者围绕多个列进行组合。

例如，new_customer字段的创建，其本质上就是围绕tenure字段进行的变换，即把所有tenure取值为1的用户都标记为1，其他用户标记为0，当然，如果我们更进一步来进行思考，这其实就是tenure字段进行独热编码后的某一列；再比如，service_num字段其本质就是所有记录各项服务购买情况的字段（先转化为数值型变量再）进行求和汇总的结果，即多列进行组合变换。

优点

模型优化利器，复杂特征衍生效果会更好

考验

建模工作者的建模经验、数据敏感度以及建模灵感的工作事项

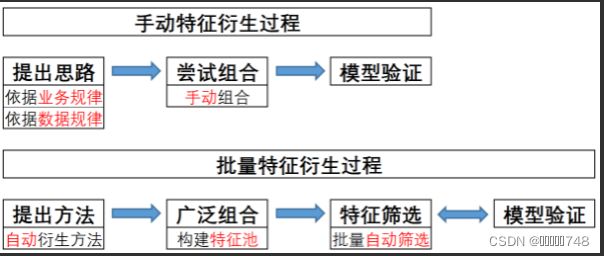
手动特征衍生与批量特征衍生

  批量特征衍生同样是数据信息的重排过程，并且执行过程上，同样也是借助单独的列进行变换或者是多个列进行组合变换。只不过不同的是，批量特征衍生并不会像手动特征衍生一样，先从思路出发、再分析数据集当前的业务背景或数据分布规律、最后再进行特征衍生，而是优先考虑从方法出发，直接考虑单个列、不同的列之间有哪些可以衍生出新特征的方法，然后尽可能去衍生出更多的特征。

  例如，我们只需要对tenure字段进行独热编码就可以一次性衍生出73个列，甚至，我们还可以随机选取tenure字段的两个不同值（例如tenure=15、17），并把这两个时间点入网的用户标记为1、其他用户标记为0，而在随机选取的情况下，这里就有[Math Processing Error]C732=73∗722=2628种特征衍生的方法。

学习阻碍

1、技术复杂

2、资料混乱

3、没有现成第三方库

策略介绍

1、四大类、26种特征衍生方法

2、双变量及多变量特征衍生策略

3、二阶及高阶特征衍生技巧

4、时序和NLP特征的衍生方法

批量特征衍生方法

1、单变量特征衍生

        解释：只需带入单独一个变量进行组合衍生

        常用方法：数据重编码特征衍生、高阶多项式特征衍生

数据重编码特征衍生

方法

        连续变量数据重编码：

               标准化：0-1标准化/Z-Score标准化

               离散化：等距分离/等频分离/聚类分箱

        离散变量数据重编码：

               标准化：自然数编码/字典编码（主要转化为数值型对象）

               离散化：独热编码（最常用，通过一列可以衍生出很多列）/哑变量变换

操作

保留原始列和重编码的列，在筛选环节中评判哪个特征更有用，也有可能两列同时带入、

高阶多项式特征衍生 

概念：

进行多项式（n次方）进行特征衍生，作为衍生的新列

实现方法：

使用sklearn里的PolynomialFeatures评估器来实现

代码执行：

import numpy as np
from sklearn.preprocessing import PolynomialFeatures
x1=np.array([1,2,4,1,3])#创建一维数组
PolynomialFeatures(degree=5).fit_transform(x1.reshape(-1,1))#创建最高次数为5的衍生列，从0开始到5次方，然后通过fit_transform对5阶进行转换，最后进行升维

结果显示：

效果：

 多特征衍生是极为常见且效果出色的特征衍生方法，在逻辑回归建模实验中，简单的多项式衍生能够将逻辑回归的决策边界由线性改善至不规则边界，从而提升模型建模效果。不过一般来说单特征的多项式效果比连续变量更有效，有时也可用于离散型随机变量

特征衍生准则

1、无限特征。

        例如N阶多项式衍生，进行分箱，再进行独热编码

2、选择依据。

模型以集成学习为主：

       ①优先考虑分类变量的独热编码，同时保留原始变量和独热编码衍生后的变量。独热编码能丰富树模型生长过程中备选的数据集切分点，进一步丰富集成学习中不同树模型可能的差异性。不适用的情况：分类变量取值水平较多（超过10个），独热编码会造成特征矩阵过于系数，影响建模效果；该离散变量参与后续多变量的交叉衍生，则无需对其进行独热编码。

       ②优先考虑连续变量的数据归一化，不会改变数据集分布（无法通过形式上的变换增加树生长的多样性），但能加快梯度下降的执行速度，加快迭代收敛的过程。

       ③如果连续变量较多，可以考虑对连续变量进行分箱。方法优先考虑聚类分箱，如果数据量过大，则可以使用MiniBatch K-Means提高效率，也可简化为等频率、等宽分箱。

       ④不建议对单变量使用多项式衍生方法，使用带有交叉项的多变量的多项式衍生方法效果会更好。

2、双变量特征衍生

        解释：需要两两组合进行组合衍生

        常用方法：四则运算特征衍生、交叉组合特征衍生、分组统计特征衍生、多项式特征衍生、统计演变特征

       补充：双变量衍生效果往往最好

四则运算特征衍生

概念：单纯的选取两列进行四则运算，加减乘除

使用场景：①用于创建业务补充字段，例如在电信用户流失数据集中时，或者房价 ②在特征衍生的所有工作结束后，对衍生出来的特征再进行四则运算特征衍生 ③在一些极为特殊的字段创建过程中使用，例如竞赛中常用的黄金组合特征，流量平滑特征。

交叉组合特征衍生

概念：不同分类变量不同取值水平之间进行交叉组合，从而创建新字段。

适用范围：一般适用于取值水平较少的分类变量。对分类变量或者取值水平将多的离散变量来说，会导致特征衍生矩阵过于稀疏，效果不佳。

代码实现

# 读取数据
tcc = pd.read_csv(r'C:\Users\86137\Desktop\WA_Fn-UseC_-Telco-Customer-Churn.csv')

# 标注连续/离散字段
# 离散字段
category_cols = ['gender', 'SeniorCitizen', 'Partner', 'Dependents',
                'PhoneService', 'MultipleLines', 'InternetService', 'OnlineSecurity', 'OnlineBackup', 
                'DeviceProtection', 'TechSupport', 'StreamingTV', 'StreamingMovies', 'Contract', 'PaperlessBilling',
                'PaymentMethod']

# 连续字段
numeric_cols = ['tenure', 'MonthlyCharges', 'TotalCharges']
 
# 标签
target = 'Churn'

# ID列
ID_col = 'customerID'

# 验证是否划分能完全
assert len(category_cols) + len(numeric_cols) + 2 == tcc.shape[1]

# 连续字段转化
tcc['TotalCharges']= tcc['TotalCharges'].apply(lambda x: x if x!= ' ' else np.nan).astype(float)
tcc['MonthlyCharges'] = tcc['MonthlyCharges'].astype(float)

# 缺失值填补
tcc['TotalCharges'] = tcc['TotalCharges'].fillna(0)

# 标签值手动转化 
tcc['Churn'].replace(to_replace='Yes', value=1, inplace=True)
tcc['Churn'].replace(to_replace='No',  value=0, inplace=True)

features = tcc.drop(columns=[ID_col, target]).copy()
labels = tcc['Churn'].copy()

category_cols

#提取目标字段
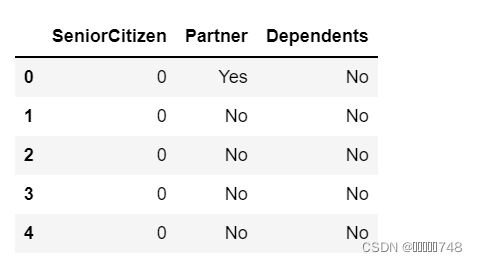
colNames=['SeniorCitizen','Partner','Dependents']
#单独提取目标字段的数据集
features_temp=features[colNames]
features_temp.head(5)

#创建空列表用于存储衍生后的特征名称和特征
colNames_new_l=[]
features_new_l=[]

#enumerate过程
for col_index,col_name in enumerate(colNames):
    print(col_index,col_name)

#衍生特征列名称
for col_index,col_name in enumerate(colNames):
    for col_sub_index in range(col_index+1,len(colNames)):
        newNames=col_name+'&'+colNames[col_sub_index]
        print(newNames)

#创建衍生特征列名称及特征本身
for col_index,col_name in enumerate(colNames):
    for col_sub_index in range(col_index+1,len(colNames)):
        newNames=col_name+'&'+colNames[col_sub_index]
        colNames_new_l.append(newNames)
        newDF=pd.Series(features[col_name].astype('str')+'&'+features[colNames[col_sub_index]].astype('str'),name=col_name)
        features_new_l.append(newDF)

features_new=pd.concat(features_new_l,axis=1)
features_new.columns=colNames_new_l
features_new

 进行独热编码

代码省略~

注意事项

无论怎样衍生，我们首先需要对衍生后的特征规模有基本判断。

分组统计特征衍生

介绍

A特征根据B特征的不同取值进行分组统计，统计量可以是均值、方差等针对连续变量的统计指标，也可以是众数、分位数等针对离散变量的统计指标

例如我们可以计算不同入网时间用户的平均月消费金额、消费金额最大值、消费金额最小值等

注意事项 

①一般来说A特征可以是离散变量也可以是连续变量，而B特征必须是离散变量，且最好是一些取值较多的离散变量（或者固定取值的连续变量）

例如本数据集中的tenure字段，总共有73个取值。主要原因是如果B特征取值较少，则在衍生的特征矩阵中会出现大量的重复的行

②在实际计算A的分组统计量时，可以不局限于连续特征只用连续变量的统计量、离散特征只用离散的统计量，完全可以交叉使用

例如A是离散变量，我们也可以分组统计其均值、方差、偏度、峰度等，连续变量也可以统计众数、分位数等。很多时候，更多的信息组合有可能会带来更多的可能性

③有的时候分组统计还可以用于多表连接的场景

例如假设现在给出的数据集不是每个用户的汇总统计结果，而是每个用户在过去的一段时间内的行为记录，则我们可以根据用户ID对其进行分组统计汇总

④很多时候我们还会考虑进一步围绕特征A和分组统计结果进行再一次的四则运算特征衍生

例如用月度消费金额减去分组均值，则可以比较每一位用户与相同时间入网用户的消费平均水平的差异，围绕衍生特征再次进行衍生，我们将其称为统计演变特征，也是分组汇总衍生特征的重要应用场景

手动实现

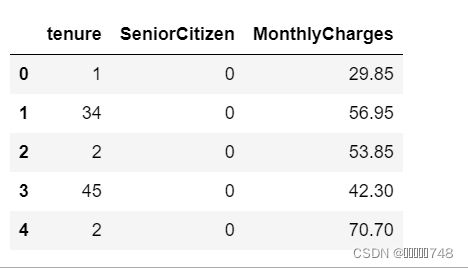
# 提取目标字段
colNames = ['tenure', 'SeniorCitizen', 'MonthlyCharges']

# 单独提取目标字段的数据集
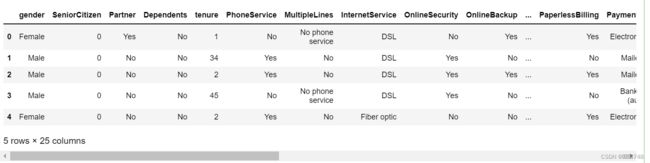
features_temp = features[colNames]
features_temp.head(5)

# 在不同tenure取值下计算其他变量分组均值的结果
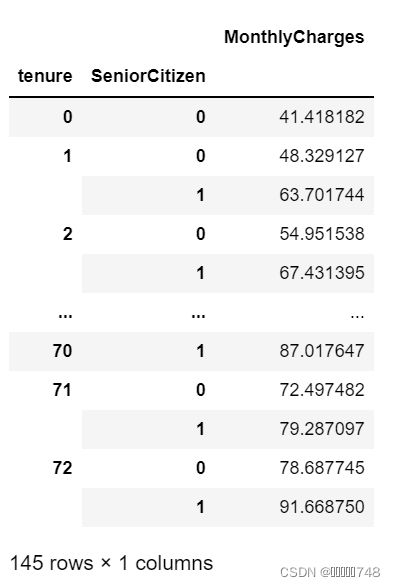
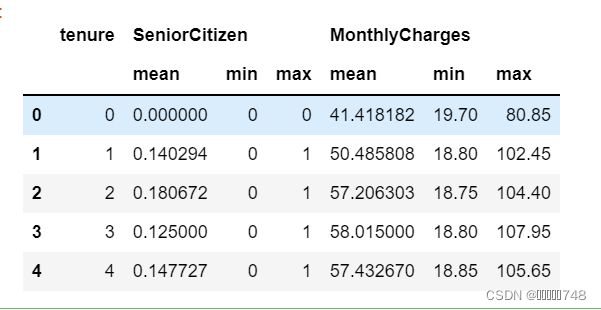
features_temp.groupby('tenure').mean()

 

# 在'tenure'、'SeniorCitizen'交叉取值分组下，计算组内月度消费金额均值
features_temp.groupby(['tenure', 'SeniorCitizen']).mean()

 

# 分组汇总字段
colNames_sub = ['SeniorCitizen', 'MonthlyCharges']

# 创建空字典
aggs = {}

# 字段汇总统计量设置
for col in colNames_sub:
    aggs[col] = ['mean', 'min', 'max']

# 每个字段汇总统计信息
aggs

 

# 创建新的列名称
cols = ['tenure']

for key in aggs.keys():
    cols.extend([key+'_'+'tenure'+'_'+stat for stat in aggs[key]])

# 创建新的列名称
cols = ['tenure']

for key in aggs.keys():
    cols.extend([key+'_'+'tenure'+'_'+stat for stat in aggs[key]])

cols

[key+'_'+'tenure'+'_'+stat for stat in aggs[key]]

features_new = features_temp.groupby('tenure').agg(aggs).reset_index()
features_new.head(5)

 

# 重新设置列名称
features_new.columns = cols
features_new.head(5)

df_temp = pd.merge(features, features_new, how='left',on='tenure')
df_temp.head()

常用统计量补充

可用于连续型变量：

mean/var:均值、方差

max/min:最大值、最小值

skew:数据分布偏度，小于零时左偏，大于零时右偏

quantile:分位数

a = np.array([[1, 2, 3, 2, 5, 1], [0, 0, 0, 1, 1, 1]])
df = pd.DataFrame(a.T, columns=['x1', 'x2'])
df

  

aggs = {'x1': ['mean', 'var', 'max', 'min', 'skew']}
df.groupby('x2').agg(aggs).reset_index()

用于分类变量：

median：中位数

count：个数统计

nunique：类别数

quantile：分位数

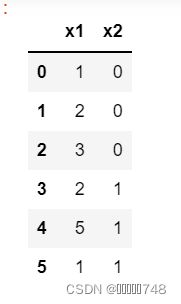
df = pd.DataFrame({'x1':[1, 3, 4, 2, 1], 'x2':[0, 0, 1, 1, 1]})
df

 

aggs = {'x1': ['median', 'count', 'nunique']}
df.groupby('x2').agg(aggs).reset_index()

 

 分位数的计算：

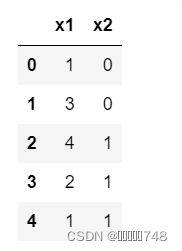
d1 = pd.DataFrame({'x1':[3, 2, 4, 4, 2, 2], 'x2':[0, 1, 1, 0, 0, 0]})
d1

aggs = {'x1': [q1, q2]}
d2 = d1.groupby('x2').agg(aggs).reset_index()
d2

d2.columns = ['x2', 'x1_x2_q1', 'x1_x2_q2']
d2

 

还有部分代码省略~ 

统计演变特征

概念

由原始特征和分组统计特征、或分组统计特征彼此之间交叉衍生而来（往往是四则运算）

原始特征与分组汇总特征交叉衍生

流量平滑特征：通过KeyCol除以分组汇总均值后的特征计算而来

黄金组合特征：简单的利用tenure减去MonthlyCharges_tenure_mean计算得出

组内归一化特征：tenure减去MonthlyCharges_tenure_mean，再除以MonthlyCharges_tenure_std，其计算过程非常类似于归一化过程，即某列数据减去该列的均值再除以该列的标准差

分组汇总特征彼此交叉衍生

Gap特征：通过分组汇总后的上四分位数-下四分位数计算得出。

数据倾斜：通过中位数和均值的比较来计算组内的数据倾斜情况：当均值大于中位数时，数据呈现正倾斜，均值小于中位数时，数据正弦负倾斜。当然衡量倾斜的方法有两种，其一是计算差值，其二则是计算比值

变异系数：通过分组统计的标准差除以均值，变异系数计算的是离中趋势，变异系数越大、说明数据离散程度越高

3、关键特征衍生（与双变量交叉使用）

        特征：时序划分与字典排序、周期划分（启止时间点划分、自然周期划分、关键时间点划分、近邻时间点划分）

        NLP特征：CountVector、TF·IDF

4、多变量特征衍生

        解释：允许同时带入三个及以上的特征进行组合衍生

        常用方法：四则运算特征衍生、交叉组合特征衍生、分组统计特征衍生

        补充：除四则运算（加法居多）的组合方法外，其他衍生方法随组合的字段的增加往往会伴随非常严重的信息衰减。

方法介绍

在单变量多项式衍生的基础上增加交叉项的计算，如二阶多项式衍生特征除一次方，二次方以外还有衍生出的任意两个变量相乘。

注意事项

①只适用于两个连续变量，或者离散变量取值水平非常多

②我们只会针对我们判断为非常重要的特征进行多项式衍生

③通常指衍生三阶，极少情况会衍生5-10阶。伴随多项式结束的增加，需要配合一些手段来消除数值绝对值爆炸或者衰减所造成的影响，如数据进行归一化

代码执行

import pandas as pd
from sklearn.preprocessing import PolynomialFeatures
df=pd.DataFrame({'X1':[1,2,3],'X2':[2,3,4]})
df

PolynomialFeatures(degree=2,include_bias=False).fit_transform(df)

结果显示：

创建了一个数据表

特征衍生出X1^2，X2^2，X1*X2

评估器PolynomialFeatures的参数

interaction——only：默认为False，如果为True，表示只创建交叉项

include——bias：默认为True，考虑计算特征的0次方，除需要人工捕捉截距，否则建议修改成False，全是1的列不包含任何有效信息。

衍生特征的排序问题：默认情况下按照第一个变量阶数依次递减、第二个变量阶数依次递增来排布

我们可以在PolynomialFeatures过程外嵌套函数，使其创建新特征的同时创建新的列的名称。

for deg in range(2,degree+1):
    for i in range(deg+1):
        col_temp=colNames[0]+'**'+str(deg-i)+'*'+colNames[1]+'**'+str(i)
        colNames_l.append(col_temp)
colNames_l

结果显示：

多变量的交叉组合特征衍生

概念：

将多个特征的不同取值水平进行组合

多变量的分组统计特征衍生

概念：

考虑采用不同离散变量的交叉组合后的取值分组依据，再进行分组统计量的计算

多变量多项式特征衍生

5、时序特征衍生

对于object对象，我们可以字符串分割的方式对其进行处理，此外还有一种更简单通用同时也更有效的方法：将其转化为datetime64格式，这也是pandas中专门用于记录时间对象的格式。对于datetime64来说有两种子类型，分别是datetime64[ns]毫秒格式与datetime64[D]日期格式。无论是哪种格式，我们可以通过pd.to_datetime函数对其进行转化

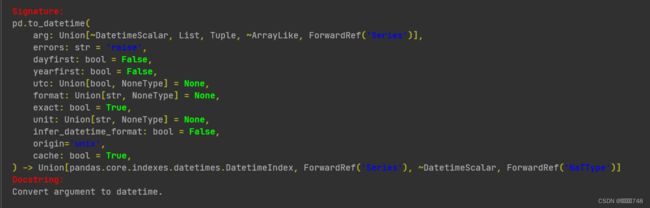
datetime函数

pd.to_datetime?

pd.to_datetime(t['time'])

dtype:datetime64[ns]  表示纳秒，=1e*10-9s

通用形式：2022-08-10；15：28：59