R语言 数据分析与可视化笔记

一、假设检验

1.正态性检验

hapiro–Wilk (夏皮罗–威克尔 ) W统计量检验

data <- c(4.33,4.62,3.89,4.14,4.78,4.64,4.52,4.55,4.48,4.26)
shapiro.test(data) #p>0.05，符合正态分布

2.方差齐性检验

R语言中方差齐性检验

（1）Bartlett检验

• 如果数据服从正态分布，那么这种方法将是最为适用的。对于正态分布的数据，这种检验极为灵敏；而当数据为非正态分布时，使用该方法则很容易导致假阳性误判。
• 多个自变量时，需用interaction()函数将多个自变量折叠为一个单一的变量用于表示不同变量因素之间的组合。bartlett.test(y~interaction(x1,x2))

high<-c(134,146,106,119,124,161,107,83,113,129,97,123)
low<-c(70,118,101,85,107,132,94)
x <- c(high,low)
group <- as.factor(c(rep("high",12),rep("low",7)))

#Bartlett检验 
bartlett.test(x~group)  #p>0.05，方差齐性

（2）Levene检验

• 相较于Bartlett检验，这一方法更为稳健。这一方法被封装于car程序包中。
• 多个自变量时，无需使用interaction函数，只需leveneTest(y~x1*x2)

high<-c(134,146,106,119,124,161,107,83,113,129,97,123)
low<-c(70,118,101,85,107,132,94)
x <- c(high,low)
group <- as.factor(c(rep("high",12),rep("low",7)))

#Levene检验
library(carData)
library(car)
leveneTest(x~group) #p>0.05，方差齐性

（3）Fligner-Killeen检验

• 非参数的检验方法，完全不依赖于对分布的假设。
• 多个自变量时，需用interaction()函数将多个自变量折叠为一个单一的变量用于表示不同变量因素之间的组合。bartlett.test(y~interaction(x1,x2))

high<-c(134,146,106,119,124,161,107,83,113,129,97,123)
low<-c(70,118,101,85,107,132,94)
x <- c(high,low)
group <- as.factor(c(rep("high",12),rep("low",7)))

#Fligner-Killeen检验
fligner.test(x~group)   #p>0.05，方差齐性

3.t检验

检验一个总体的均值是否为某数，或两总体均值是否相同。
前提假设：正态，方差齐性
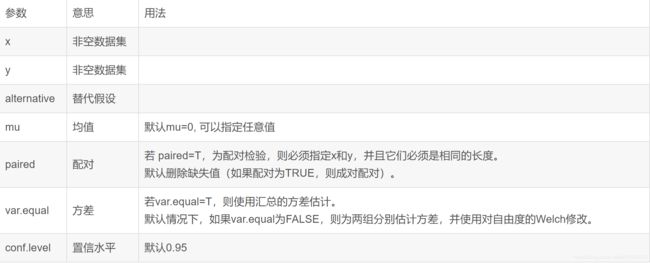
t检验算法及其在R语言中的实现

t.test(x, y = NULL,
       alternative = c("two.sided", "less", "greater"), 
       mu = 0, paired = FALSE, var.equal = FALSE,
       conf.level = 0.95, ...)

（1）单样本t检验

data <- c(4.33,4.62,3.89,4.14,4.78,4.64,4.52,4.55,4.48,4.26)

#正态性检验，W检验
shapiro.test(data) #p>0.05，符合正态分布

#单样本t检验
t.test(data,mu=4.5) #H0:均值=mu
#p>0.05,不拒绝原假设，认为均值=mu

（2）两样本t检验

非成对两样本t检验

high<-c(134,146,106,119,124,161,107,83,113,129,97,123)
low<-c(70,118,101,85,107,132,94)
x <- c(high,low)
group <- as.factor(c(rep("high",12),rep("low",7)))

#正态性检验
shapiro.test(high)
shapiro.test(low)

#方差齐性检验
library(carData)
library(car)
leveneTest(x~group) #p>0.05，方差齐性

#非成对两样本T检验
t.test(high,low,paired = FALSE,var.equal = T)

成对两样本t检验

ds <- c(82.5,85.2,87.6,89.9,89.4,90.1,87.8,87.0,88.5,92.4)
cs <- c(91.7,94.2,93.3,97.0,96.4,91.5,97.2,96.2,98.5,95.8)
x<-c(ds,cs)
group<-as.factor(c(rep("ds",length(ds)),rep("cs",length(cs))))

#方差齐性检验
library(carData)
library(car)
leveneTest(x~group) #p>0.05，方差齐性

#正态性检验
d <- ds-cs
shapiro.test(d)

t.test(ds,cs,paired = T,alternative = "two.sided",cond.lvel=0.95)

4.卡方检验

检验两个变量之间有没有关系，非参数检验
使用R语言进行卡方检验

library(survival)
data(colon)
mytable <- xtabs(~ status + sex, data= colon)
mytable

#卡方检验
chisq.test(mytable)  # 进行连续性校正
chisq.test(mytable, correct = FALSE) # 不进行连续性校正
#p>0.05,不拒绝原假设，认为sex和status无关

5.方差分析

R中的方差分析ANOVA（一）
R中的方差分析ANOVA（二）
多个总体的均值比较
前提假设：正态、方差齐性

（1）单因素方差分析

medicine <- data.frame(
  Response=c(30,38,35,41,27,24,32,26,31,29,27,35,21,25,17,21,20,19),
  Treatment=factor(c(rep("a",6),rep("b",8),rep("c",4)))
)
attach(medicine)

#正态性检验
shapiro.test(Response[Treatment=="a"])
shapiro.test(Response[Treatment=="b"])
shapiro.test(Response[Treatment=="c"])

#方差齐性检验
bartlett.test(Response~Treatment,data=medicine)

a.aov <- aov(Response~Treatment,data = medicine)
summary(a.aov) #p<0.0.5,拒绝原假设，各水平的均值存在显著差异。

# 各水平均值
print(model.tables(a.aov,"means"),digits=3)

多重比较

TukeyHSD(a.aov)

#结果：
  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = Response ~ Treatment, data = medicine)

$Treatment
      diff       lwr       upr     p adj
b-a  -4.25 -11.15796  2.657961 0.2768132
c-a -13.25 -21.50659 -4.993408 0.0022342
c-b  -9.00 -16.83289 -1.167109 0.0237003

## a和c,b和c存在显著差异，他们的P值<0.05.

使用调整的p值

pairwise.t.test(Response,Treatment,p.adjust.method = "bonferroni")

#结果：
	Pairwise comparisons using t tests with pooled SD 

data:  Response and Treatment 

  a      b     
b 0.3926 -     
c 0.0025 0.0278

P value adjustment method: bonferroni 

## c与a,b存在显著差异，a与b无显著差异

（2）多因素方差分析

x=c(8,12,13,12,6,7,23,14,15,12,22,14,15,12,18,22)
sales=data.frame(x,A=c(rep("m",8),rep("f",8)),B=c(rep("a",4),rep("b",4),rep("a",4),rep("b",4)))
attach(sales)

#分别对A,B变量方差齐性检验
bartlett.test(sales$x,sales$A)
bartlett.test(sales$x,sales$B)

#无交互
x.aov <- aov(x~A+B,data = sales)
summary(x.aov)

#有交互
sales.aov <- aov(x ~A+B+A:B,data = sales)
summary(sales.aov)
#所有p值>0.05,各因素之间无显著差异，也无交互作用

interaction.plot(A,B,x,legend=F)
interaction.plot(B,A,x,legend=F)
# 曲线均没有相交，初步判断两因素之间无交互作用

#用effects包来查看A,B 的交互效应
library(effects)
plot(effect(c("A","B"),sales.aov),multiline=TRUE)
# 曲线均没有相交，两因素之间无交互作用

6.秩和检验

总体不是正态，检验多个总体的分布是否相同

（1）两样本：wilcoxon秩和检验

#wilcoxon秩和检验
data("mtcars")
wilcox.test(mpg~am,data = mtcars) # p值<0.05,原假设不成立，两总体分布不同

（2）多样本：Kruskal-Wallis秩和检验

medicine <- data.frame(
  Response=c(7,5,3,1,6,5,3,3,7,9,9,9,4,3,4,3),
  Treatment=factor(c(rep(1,4),rep(2,4),rep(3,4),rep(4,4)))
)
attach(medicine)

#正态性检验
shapiro.test(Response[Treatment=='1'])
shapiro.test(Response[Treatment=='2'])
shapiro.test(Response[Treatment=='3'])
shapiro.test(Response[Treatment=='4'])
#3和4的p值<0.05。不符合正态

kruskal.test(Response~Treatment,data=medicine) #P<0.05，拒绝原假设，认为四个水平存在显著差异

二、作图

1.散点图

快速作图和ggplot2

plot(mtcars$wt,mtcars$mpg)

qplot(mtcars$wt,mtcars$mpg)
qplot(wt,mpg,data=mtcars)

sq<-ggplot(heightweight,aes(x=ageYear,y=heightIn))
sq+geom_point(shape=21,size=1.5)

分组变量（factor或字符）&连续变量，映射到颜色/点型/大小

ggplot(heightweight,aes(x=ageYear,y=heightIn,color=sex,shape=sex))+geom_point(size=1.5)

#使用其他点型和颜色
ggplot(heightweight,aes(x=ageYear,y=heightIn,color=sex,shape=sex))+geom_point(size=1.5)+scale_shape_manual(values=c(1,4))+scale_color_brewer(palette = "Set1")

#连续变量用于涂色
ggplot(heightweight,aes(x=ageYear,y=heightIn,fill=weightLb))+geom_point(shape=21,size=2.5)+scale_fill_gradient(low='black',high='white',breaks=seq(70,170,by=20),guide=guide_legend())

添加拟合线

sp<-ggplot(heightweight,aes(x=ageYear,y=heightIn))
sp+geom_point(shape=21,size=1.5)+stat_smooth(method=lm,level=0.95) #95的置信域
sp+geom_point(shape=21,size=1.5)+stat_smooth(method=lm,se=FALSE,color='Black') #无置信域

#method设置拟合模型，默认method=loess（局部加权多项式），还可以glm（逻辑回归）

根据已有模型添加拟合线

model<-lm(heightIn~ageYear+I(ageYear^2),heightweight) #带二阶项的线性回归

#生成拟合线的点的横坐标
xmin<-min(heightweight$ageYear)
xmax<-max(heightweight$ageYear)
predicted<-data.frame(ageYear=seq(xmin,xmax,length.out = 100))

#生成拟合线的点的纵坐标
predicted$heightIn<-predict(model,predicted)

#画图
sq<-ggplot(heightweight,aes(x=ageYear,y=heightIn))
sq+geom_point()+geom_line(data=predicted)

#函数封装上述功能
predictvals <- function(model, xvar, yvar, xrange = NULL, samples = 100, ...)
{
  if(is.null(xrange)) #如果未输入xrange,自动提取x轴范围
  {
    if(any(class(model) %in% c("lm","glm"))) #如果是线性回归或广义线性模型
      xrange <- range(model$model[[xvar]])
    else if(any(class(model) %in% "loess")) #如果是局部加权多项式模型
      xrange <- range(model$x)
  }
  newdata <- data.frame(x = seq(xrange[1], xrange[2], length.out = samples))
  names(newdata) <- xvar
  newdata[[yvar]] <- predict(model, newdata = newdata, ...)
  newdata
}

lm_predicted<-predictvals(model,'ageYear','heightIn')
sq+geom_point()+geom_line(data=lm_predicted)

分组添加拟合线

make_model<-function(data){
  lm(heightIn~ageYear,data)
}

#返回分组的拟合模型
library(plyr)
models<-dlply(heightweight,.variables = 'sex',.fun=make_model)

#返回分组的预测值
predvals<-ldply(models,.fun=predictvals,xvar='ageYear',yvar='heightIn')

#画图
sq<-ggplot(heightweight,aes(x=ageYear,y=heightIn,color=sex))
sq+geom_point()+geom_line(data=predvals)

2.折线图

快速作图和ggplot

plot(pressure$temperature,pressure$pressure,type="l")
points(pressure$temperature,pressure$pressure)
lines(pressure$temperature,pressure$pressure/2,col="red")
points(pressure$temperature,pressure$pressure/2,col="red")

qplot(pressure$temperature,pressure$pressure,geom='line')
qplot(pressure$temperature,pressure$pressure,geom=c('point','line'))

ggplot(pressure,aes(x=temperature,y=pressure))+geom_line()
ggplot(pressure,aes(x=temperature,y=pressure))+geom_point()+geom_line()

3.条形图

快速作图和ggplot

#条形图
barplot(BOD$demand,names.arg = BOD$Time)
ggplot(BOD,aes(x=Time,y=demand))+geom_bar(stat='identity')

#频数条形图
barplot(table(mtcars$cyl)) 
ggplot(mtcars,aes(x=factor(cyl)))+geom_bar()

4.箱线图

快速作图和ggplot

boxplot(len~supp,data=ToothGrowth)
boxplot(len~supp+dose,data=ToothGrowth) #加交互

qplot(supp,len,data=ToothGrowth,geom='boxplot')
qplot(interaction(supp,dose),len,data=ToothGrowth,geom='boxplot')

ggplot(ToothGrowth,aes(x=supp,y=len))+geom_boxplot()
ggplot(ToothGrowth,aes(x=interaction(supp,dose),y=len))+geom_boxplot()

三、模型

1.线性回归

x1 <- rnorm(20,mean = 5,sd = 1)
x2 <- rnorm(20,mean = 10,sd = 1)
y <- 3*x1+4*x2+rnorm(20,mean = 0,sd = 1)
data1 <- data.frame('x1'=x1,'x2'=x2,'y'=y)
fit1 <- lm(y~x1+x2-1,data=data1)  #-1表示不带截距项，如果不写则带截距项
#查看拟合结果
summary(fit1)
#残差图
par(mfrow=c(2,2))
plot(fit1)

2.逻辑回归

iris1<-iris[iris$Species!="setosa",]
levels(iris1$Species)

#将数据分成训练集和测试集,利用caTools将数据切割
library(caTools)
TB<-sample.split(iris1$Species,2/3)
iris1.train<-iris1[TB,]
iris1.test<-iris1[!TB,]

#建模
result<-glm(Species~.,data=iris1.train,family="binomial")
summary(result)

#预测
predResult<-round(predict(result,iris1.test,type="response"))
predResult
predResult<-factor(predResult,levels=c(0,1),labels=c("versicolor","virginica"))
predResult

mean(predResult==iris1.test$Species)

3.主成分分析

test<-data.frame(
  X1=c(148, 139, 160, 149, 159, 142, 153, 150, 151, 139,
       140, 161, 158, 140, 137, 152, 149, 145, 160, 156,
       151, 147, 157, 147, 157, 151, 144, 141, 139, 148),
  X2=c(41, 34, 49, 36, 45, 31, 43, 43, 42, 31,
       29, 47, 49, 33, 31, 35, 47, 35, 47, 44,
       42, 38, 39, 30, 48, 36, 36, 30, 32, 38),
  X3=c(72, 71, 77, 67, 80, 66, 76, 77, 77, 68,
       64, 78, 78, 67, 66, 73, 82, 70, 74, 78,
       73, 73, 68, 65, 80, 74, 68, 67, 68, 70),
  X4=c(78, 76, 86, 79, 86, 76, 83, 79, 80, 74,
       74, 84, 83, 77, 73, 79, 79, 77, 87, 85,
       82, 78, 80, 75, 88, 80, 76, 76, 73, 78)
)

test.pr<-princomp(~X1+X2+X3,data=test,cor=TRUE)  #cor是逻辑变量 当cor=TRUE表示用样本的相关矩阵R做主成分分析,当cor=FALSE表示用样本的协方差阵S做主成分分析
summary(test.pr,loadings=TRUE)  #loading是逻辑变量 当loading=TRUE时表示显示loading 的内容
screeplot(test.pr,type="lines")
p<-predict(test.pr) #所有样本的主成分

#前两个主成分累计贡献率到了97%，只取前两个做回归
test$z1<-p[,1]
test$z2<-p[,2]
lm.sol<-lm(X4~z1+z2,data=test)
summary(lm.sol)

predict(lm.sol,data=p) #预测结果