Keras入门教程 2.线性模型的优化
Keras入门教程
- 1.线性回归建模(快速入门)
- 2.线性模型的优化
- 3.波士顿房价回归 (MPL)
- 4.卷积神经网络(CNN)
- 5.使用LSTM RNN 进行时间序列预测
- 6.Keras 预训练模型应用
线性模型的优化
前言
上一节,我们讲解了,keras 的实现过程,本节在原来的基础上添加相应层,增加优化器,以达到优化模型的目的。
正文
仍以上一节的数据集作为分析,以下部分均与上一节一致
### 加载包
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error
%matplotlib inline
### 数据导入
data=pd.DataFrame(columns=['Education','Income'],data=[[10.00000,26.65884],
[10.40134,27.30644],
[10.84281,22.13241],
[11.24415,21.16984],
[11.64548,15.19263],
[12.08696,26.39895],
[12.48829,17.43531],
[12.88963,25.50789],
[13.29097,36.88459],
[13.73244,39.66611],
[14.13378,34.39628],
[14.53512,41.49799],
[14.97659,44.98157],
[15.37793,47.03960],
[15.77926,48.25258],
[16.22074,57.03425],
[16.62207,51.49092],
[17.02341,61.33662],
[17.46488,57.58199],
[17.86622,68.55371],
[18.26756,64.31093],
[18.70903,68.95901],
[19.11037,74.61464],
[19.51171,71.86720],
[19.91304,76.09814],
[20.35452,75.77522],
[20.75585,72.48606],
[21.15719,77.35502],
[21.59866,72.11879],
[22.00000,80.26057]])
X=data.Education.values.reshape(-1,1)
y=data.Income
keras 建模
加载包
from keras.models import Sequential
from keras.layers import Densef
from tensorflow.keras.optimizers import RMSprop
这里需要特别说的是
from tensorflow.keras.optimizers import RMSprop在很多博客或文章是from keras.optimizers import RMSprop运行报错,是因为我们这里是采用 tensorflow 作为后端,而非单独安装 keras 引起的,特此说明。
为了方便说明,以下代码将上节的模型名称修改为model
model = Sequential()
model.add(Dense(64, kernel_initializer = 'normal', activation = 'relu',input_shape = (1,))) # 增加了激活函数 relu
model.add(Dense(128, activation = 'relu')) # 增加了层
model.add(Dense(1))
查看模型
model_kr.summary()
Model: “sequential_3”
Layer (type) Output Shape Param #
dense_8 (Dense) (None, 64) 128
dense_9 (Dense) (None, 64) 4160
dense_10 (Dense) (None, 1) 65
=================================================================
Total params: 4,353
Trainable params: 4,353
Non-trainable params: 0
选择损失函数和优化方法
# model_kr.compile(optimizer='adam' , loss='mse') 原来的
model.compile(
loss = 'mse', # 损失函数
optimizer = RMSprop(), # 优化器
metrics = ['mean_absolute_error'] # 衡量指标
)
进行拟合训练
history= model.fit(X , y , epochs=200 , verbose=1)
进行200次的结果如下
Epoch 1/200
1/1 [==============================] - 2s 2s/step - loss: 112.1887 - mean_absolute_error: 8.9837
Epoch 2/200
1/1 [==============================] - 0s 11ms/step - loss: 121.1905 - mean_absolute_error: 8.8568
Epoch 3/200
1/1 [==============================] - 0s 17ms/step - loss: 111.5530 - mean_absolute_error: 8.9720
Epoch 4/200
1/1 [==============================] - 0s 14ms/step - loss: 111.3915 - mean_absolute_error: 8.9431
Epoch 5/200
1/1 [==============================] - 0s 14ms/step - loss: 111.2669 - mean_absolute_error: 8.9382
Epoch 6/200
1/1 [==============================] - 0s 15ms/step - loss: 111.1435 - mean_absolute_error: 8.9319
Epoch 7/200
1/1 [==============================] - 0s 12ms/step - loss: 111.0212 - mean_absolute_error: 8.9259
Epoch 8/200
1/1 [==============================] - 0s 11ms/step - loss: 110.8999 - mean_absolute_error: 8.9200
Epoch 9/200
1/1 [==============================] - 0s 12ms/step - loss: 110.7795 - mean_absolute_error: 8.9140
Epoch 10/200
1/1 [==============================] - 0s 11ms/step - loss: 110.6598 - mean_absolute_error: 8.9082
Epoch 11/200
1/1 [==============================] - 0s 17ms/step - loss: 110.5408 - mean_absolute_error: 8.9023
Epoch 12/200
1/1 [==============================] - 0s 12ms/step - loss: 110.4224 - mean_absolute_error: 8.8965
Epoch 13/200
1/1 [==============================] - 0s 11ms/step - loss: 110.3046 - mean_absolute_error: 8.8908
...
Epoch 199/200
1/1 [==============================] - 0s 8ms/step - loss: 89.9502 - mean_absolute_error: 7.7671
Epoch 200/200
1/1 [==============================] - 0s 7ms/step - loss: 89.8372 - mean_absolute_error: 7.8902
yks_pred=model_kr.predict(X) # model_kr 此为上一节模型 (需要用到上节模型)
yks_pred1=model.predict(X)
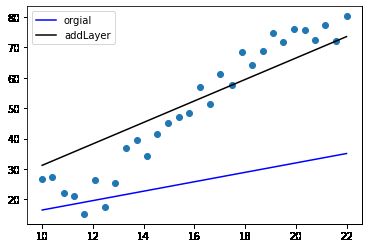
看看回归曲线
plt.scatter(X,y)
plt.plot(X,yks_pred,"b",label='orgial')
plt.plot(X,yks_pred1,"r",label='addLayer')
plt.legend()
效果如此显,还有更多的提升空间
再次增加epoch次数
再次训练可以再调用以下语句
history= model.fit(X , y , epochs=200 , verbose=1)
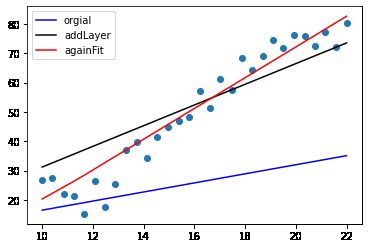
再多次运行fit结果如下:
特别提醒初学者小伙伴,千万别一次性将
epochs值调到很大的值,否则你的电脑死在那里了(原因是吃光你的内存)。你可以多次的调用上述代码,查看学习效果。
小节
现在有一个比较令人满意的结果了,随着练习次数的增加,模型提升的效果会越越小,也就是说模型不可能是无休止的提升,到达一定程度就不可能再提升了。这是由于数据集本身决定的,并非模型决定的。理论上讲,只要数据量大,深度学习一定能达到数据集本身理想上限。
理论部分
讲了这么多,应该对深度学习有些感性的认识,现在开始讲一讲最最简单的理解原理部。
我也不想把问题讲得太复杂,先看一下下面这张图,神经元模型(引自 周志华《机器学习》)
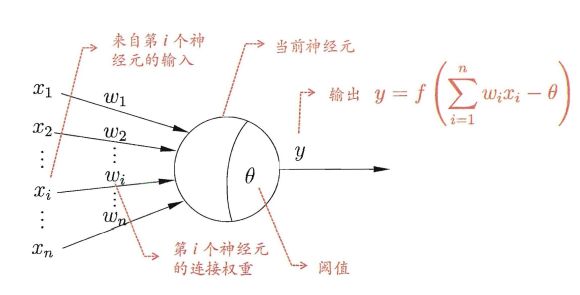
转化为下图的模型,这样的话,大伙比较真观了解其结构。
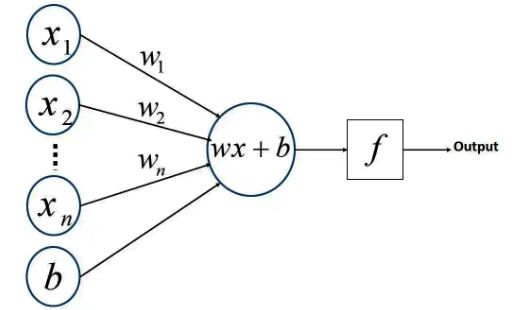
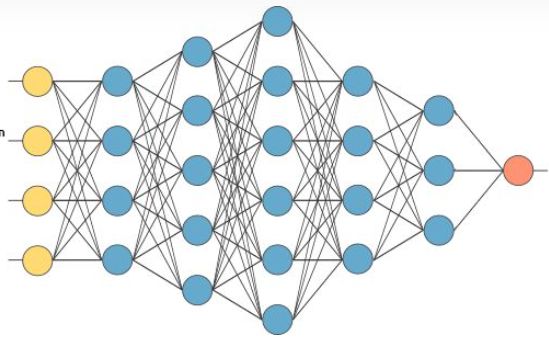
由于上图只是一个神经元结构,在真正的深度学习体系中,可能用到好多个神经元,分成很多层,始下图,黄色部分为输入层,蓝色部分为中间层,又称隐藏层,橙色部分为输出层,有时输出层也有可能是多变量的。
总结
真正的深度学习模型,需要不同的层,不同的损失函数,激活函数等,才现达到最优的效果。
很上例,增加了层,模型有明显的提升效果。
下一节,将以此模型,在 波士顿 房价数据集上做进一步探讨,以达到学习的目的。