博弈论（Nim游戏、有向图游戏之SG函数）

经典NIM游戏

模板题 AcWing 891. Nim游戏

给定N堆物品，第i堆物品有Ai个。两名玩家轮流行动，每次可以任选一堆，取走任意多个物品，可把一堆取光，但不能不取。取走最后一件物品者获胜。两人都采取最优策略，问先手是否必胜。

我们把这种游戏称为NIM博弈。把游戏过程中面临的状态称为局面。整局游戏第一个行动的称为先手，第二个行动的称为后手。若在某一局面下无论采取何种行动，都会输掉游戏，则称该局面必败。
所谓采取最优策略是指，若在某一局面下存在某种行动，使得行动后对面面临必败局面，则优先采取该行动。同时，这样的局面被称为必胜。我们讨论的博弈问题一般都只考虑理想情况，即两人均无失误，都采取最优策略行动时游戏的结果。
NIM博弈不存在平局，只有先手必胜和先手必败两种情况。

定理： NIM博弈先手必胜，当且仅当 A1 ^ A2 ^ … ^ An != 0

Nim游戏属于公平组合游戏ICG

若一个游戏满足：

1. 由两名玩家交替行动；
2. 在游戏进程的任意时刻，
3. 可以执行的合法行动与轮到哪名玩家无关； 不能行动的玩家判负；

则称该游戏为一个公平组合游戏。
NIM博弈属于公平组合游戏，但城建的棋类游戏，比如围棋，就不是公平组合游戏。因为围棋交战双方分别只能落黑子和白子，胜负判定也比较复杂，不满足条件2和条件3。

有向图游戏(SG函数）

给定一个有向无环图，图中有一个唯一的起点，在起点上放有一枚棋子。两名玩家交替地把这枚棋子沿有向边进行移动，每次可以移动一步，无法移动者判负。该游戏被称为有向图游戏。
任何一个公平组合游戏都可以转化为有向图游戏。具体方法是，把每个局面看成图中的一个节点，并且从每个局面向沿着合法行动能够到达的下一个局面连有向边。

（以当前局面作为图中的一个节点，由当前局面可以到达的局面作为当前节点的后继节点，那么整体就可以形成一个图的结构，这样的一个公平组合游戏就形成了一个“有向图游戏”。）

Mex运算

设S表示一个非负整数集合。定义mex(S)为求出不属于集合S的最小非负整数的运算，即：
mex(S) = min{x}, x属于自然数，且x不属于S

SG函数

在有向图游戏中，对于每个节点x，设从x出发共有k条有向边，分别到达节点$y_1,y_2,\dots ,y_k$，定义SG(x)为x的后继节点 $y_1,y_2,\dots ,y_k$ 的SG函数值构成的集合再执行$mex(S)$运算的结果，即：
$SG(x)=mex(SG(y_1),SG(y_2),\dots ,SG(y_k))$
特别地，整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值，即$SG(G)=SG(s)$。

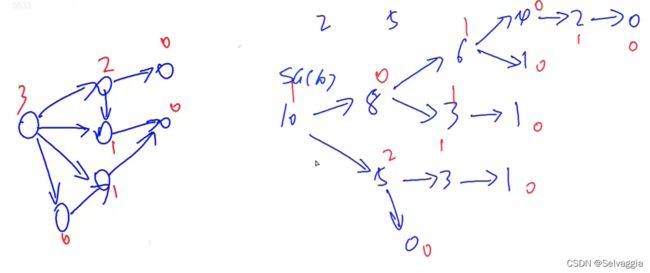
单个有向图（一堆石子）

定理
有向图游戏的某个局面必胜，当且仅当该局面对应节点的SG函数值大于0。
有向图游戏的某个局面必败，当且仅当该局面对应节点的SG函数值等于0。

如上图所示，当仅有一堆石子时，如果SG(初始局面对应的点）≠0，先手必胜，为零则必败
原因：
SG值经过了Mex运算，倘若SG（s）不为0，s所有的后继局面对应的点之中，必定有一点SG值为0，
当走到SG值为0的这一点时，根据Mex运算，该点所连接的所有点的值中一定不存在SG值为0的后继局面，只要先手面对的局面的SG值不为0，如此往复，先手一定会走到最后的终点（终止状态的SG的值定义为0）

1. 终止状态的SG的值定义为0
2. SG值为0的点为必败态，它的后继节点中不存在SG值为0的点
3. SG值非0的点为必胜态，它的后继节点中存在一点SG值为0

求SG值（记忆化递归）

#include  
const int N=105;
const int M=10005;
int k;
int s[N];//选取数的集合 
int n,v;
int f[M];//记忆化递归，记录每个有向图当下局面的SG值
//f存储的是所有可能出现过的局面的sg值，
//因为每个局面的SG值都要由她所有后继局面的SG值决定 
int SG(int x){
	if(f[x]!=-1)return f[x];
//每个局面的sg值都是确定的,如果存储过了,直接返回即可
	set<int> S;
//只针对当下一个局面，存放这个局面的若干后继局面
//每个局面都会新定义一个set集合 
	for(int i=0;i<k;i++){//枚举每一个可能的后继局面，把后继局面的SG值放到x对应的set集合中 
		int ss=s[i];
		if(x>=ss){
			S.insert(SG(x-ss));
//先延伸到终点的sg值后,再回溯得出所有数的sg值 
//记忆化递归，先求出终点sg值，再从后往前
		}
	}
	for(int i=0;;i++){//选没有出现在 x的后继局面的SG值中的 最小自然数 
		if(S.count(i)==0){
			f[x]=i;
			return f[x];
		}
	} 
} 

有向图游戏的和 ，（多个有向图（多堆石子）

设G1, G2, …, Gm 是m个有向图游戏。定义有向图游戏G，它的行动规则是任选某个有向图游戏Gi，并在Gi上行动一步。G被称为有向图游戏G1, G2, …, Gm的和。

有向图游戏的和的SG函数值等于它包含的各个子游戏SG函数值的异或和，即： SG(G) = SG(G1) ^ SG(G2) ^ … ^
SG(G_m)

证明：（同Nim游戏）
1.终止状态为异或和为0的局面，显然是先手必败局面（当最终每一堆石子都无法操作时，每一堆的SG值为0），满足SG定理

2.由各个有向图当下局面的SG异或和不为0，采取类似Nim游戏中的最佳决策，一定可以到异或和为0的状态
异或和x不为0，x必定存在最高位（第k位）的1，必定存在第k位为1的SGi，SGi > SGi ^ x, 让SGi 变为 SGi ^ x
小于SGi的非负整数都属于SGi的后继节点

3.由异或和为0的状态只能到达异或和不为0的状态

本着最佳决策，面对异或和非零的局面，理应在第i个有向图中，将状态由SGi转到 SGi ^ x (各有向图的异或值）从而把异或和为0的局面抛给对手，
可是，对于以下解释，我没懂为啥，将SGi移动到SG值更大的节点 SGi’ 时，另一方一定可以找到和 SGi’相等的另一个有向图且有着SGi 的后继状态？？？

模板题 AcWing 893. 集合-Nim游戏

#include 
#include 
#include 
using namespace std;
#include  
const int N=105;
const int M=10005;
int k;
int s[N];//选取数的集合 
int n,v;
int f[M];//记忆化递归，记录每个有向图当下局面的SG值
//f存储的是所有可能出现过的局面的sg值，
//因为每个局面的SG值都要由她所有后继局面的SG值决定 
int SG(int x){
	if(f[x]!=-1)return f[x];
//每个局面的sg值都是确定的(因为对于确定的石子数，可取的方案只有S数组中存的那几种，石子数相同的状态后续局面一定完全相同，对应的SG值一定相同,如果存储过了,直接返回即可
//这里更好解释为什么存放SG值的f数组的范围由最大石子数决定
	set<int> S;
//只针对当下一个局面，存放这个局面的若干后继局面
//每个局面都会新定义一个set集合 
	for(int i=0;i<k;i++){//枚举每一个可能的后继局面，把后继局面的SG值放到x对应的set集合中 
		int ss=s[i];
		if(x>=ss){
			S.insert(SG(x-ss)); 
	//先延伸到终点的sg值后,再回溯得出所有数的sg值 
		}
	}
	for(int i=0;;i++){//选没有出现在 x的后继局面的SG值中的 最小自然数 
		if(S.count(i)==0){
			f[x]=i;
			return f[x];
		}
	} 
} 
int main(){
	cin>>k;
	for(int i=0;i<k;i++)cin>>s[i];
	cin>>n;
//	fill(f,f+n,-1);
	memset(f,-1,sizeof(f));
	int res=0;
	
	for(int i=0;i<n;i++){
		cin>>v;
		res^=SG(v);
	}
	if(res)cout<<"Yes";
	else cout<<"No"; 
    return 0;
}

练兵时间到（习题集）

game（取后可分为两堆 (x^y<=x+y)

Game

Time Limit:1000MS Memory Limit:65536KB

Description

Here is a game for two players. The rule of the game is described below:

● In the beginning of the game, there are a lot of piles of beads.

● Players take turns to play. Each turn, player choose a pile i and remove some (at least one) beads from it. Then he could do nothing or split pile i into two piles with a beads and b beads.(a,b > 0 and a + b equals to the number of beads of pile i after removing)

● If after a player’s turn, there is no beads left, the player is the winner.

Suppose that the two players are all very clever and they will use optimal game strategies. Your job is to tell whether the player who plays first can win the game.

Input

There are multiple test cases. Please process till EOF.

For each test case, the first line contains a postive integer n(n < 10 5) means there are n piles of beads. The next line contains n postive integer, the i-th postive integer a i(a i < 2 31) means there are a i beads in the i-th pile.

Output

For each test case, if the first player can win the game, ouput “Win” and if he can’t, ouput “Lose”

Sample Input

1

1

2

1 1

3

1 2 3

Sample Output

Win

Lose

Lose

这道题是典型的Nim游戏，与Nim游戏不同的是该题中除了至少拿走一颗珠子以外，拿完之后还可以什么都不做，或者，将该堆剩下的珠子分为两堆。
其实这对游戏的胜负判断是没有影响的。因为，对于后手，面对异或和为0的局面，至少拿走了一颗珠子，那么xor求和，之前为0，拿走珠子以后，无论是否将剩下的该堆珠子分为两堆，此时的xor和必不为零（解释见下方），反之亦然。

Nim游戏通俗地说就是：
如果异或的结果为0，那么改变任何一个数，显然结果肯定不能为0了，如果结果不为0，改变某个特定一个数，可以使结果等于0，而异或运算恰好就满足这个条件。因而成就了这个不可思议的定理。

大概，两个数X，Y，X^Y 的结果只会 小于等于 X+Y，如下
所以，对于先手，只需要改变特定的一堆，把异或和为0的局面抛给后手，而对于后手，面对着异或和为0的局面，且必须要取走一堆中大于0的石子，取完后，无论是否分为两堆，异或和都不为0
假设后手取的第i堆原先有Si个石子，取完后有Si’ 个， Si > Si’=X+Y
不分为两堆，Si’ 不可能等于Si
分为两堆，X^Y 不可能得到 Si（Si>X +Y)
10
01
——
11

101
010
——
111

111
010
——
101

S-Nim + sg函数+博弈+模板（vis数组代替set

S-Nim
Time Limit: 5000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2898 Accepted Submission(s): 1288

Problem Description
Arthur and his sister Caroll have been playing a game called Nim for some time now. Nim is played as follows:

The starting position has a number of heaps, all containing some, not necessarily equal, number of beads.

The players take turns chosing a heap and removing a positive number of beads from it.

The first player not able to make a move, loses.

Arthur and Caroll really enjoyed playing this simple game until they recently learned an easy way to always be able to find the best move:

Xor the number of beads in the heaps in the current position (i.e. if we have 2, 4 and 7 the xor-sum will be 1 as 2 xor 4 xor 7 = 1).

If the xor-sum is 0, too bad, you will lose.

Otherwise, move such that the xor-sum becomes 0. This is always possible.

It is quite easy to convince oneself that this works. Consider these facts:

The player that takes the last bead wins.

After the winning player’s last move the xor-sum will be 0.

The xor-sum will change after every move.

Which means that if you make sure that the xor-sum always is 0 when you have made your move, your opponent will never be able to win, and, thus, you will win.

Understandibly it is no fun to play a game when both players know how to play perfectly (ignorance is bliss). Fourtunately, Arthur and Caroll soon came up with a similar game, S-Nim, that seemed to solve this problem. Each player is now only allowed to remove a number of beads in some predefined set S, e.g. if we have S =(2, 5) each player is only allowed to remove 2 or 5 beads. Now it is not always possible to make the xor-sum 0 and, thus, the strategy above is useless. Or is it?

your job is to write a program that determines if a position of S-Nim is a losing or a winning position. A position is a winning position if there is at least one move to a losing position. A position is a losing position if there are no moves to a losing position. This means, as expected, that a position with no legal moves is a losing position.

Input
Input consists of a number of test cases. For each test case: The first line contains a number k (0 < k ≤ 100 describing the size of S, followed by k numbers si (0 < si ≤ 10000) describing S. The second line contains a number m (0 < m ≤ 100) describing the number of positions to evaluate. The next m lines each contain a number l (0 < l ≤ 100) describing the number of heaps and l numbers hi (0 ≤ hi ≤ 10000) describing the number of beads in the heaps. The last test case is followed by a 0 on a line of its own.

Output
For each position: If the described position is a winning position print a ‘W’.If the described position is a losing position print an ‘L’. Print a newline after each test case.

Sample Input

2 2 5
3
2 5 12
3 2 4 7
4 2 3 7 12
5 1 2 3 4 5
3
2 5 12
3 2 4 7
4 2 3 7 12
0

#include 
#include 
#include 
#include 
 
using namespace std;
 
int sg[10010];
int s[110];
int k,m,l;
 
int mex(int x)
{
    if(sg[x]!=-1)return sg[x];
    bool vis[110]; //一定要将vis数组定义到这里
    memset(vis,false,sizeof(vis));
    for(int i=0;i<k;i++){
        int temp=x-s[i];
        if(temp<0)break;//此处因为s[i]排好序的，所以后面temp的值肯定小于0，所以直接跳出就可以。
        sg[temp]=mex(temp);
        vis[sg[temp]]=true;
    }
    for(int i=0;;i++){
        if(!vis[i]){
            sg[x]=i;
            break;
        }
    }
    return sg[x];
}
int main()
{
    while(scanf("%d",&k),k)
    {
        int res[110];
        memset(res,0,sizeof(res));
        memset(sg,-1,sizeof(sg));
        sg[0]=0;
        for(int i=0;i<k;i++)
            scanf("%d",&s[i]);
        sort(s,s+k);
        scanf("%d",&m);
        int a;
        for(int i=0;i<m;i++){
            scanf("%d",&l);
            for(int j=0;j<l;j++){
                scanf("%d",&a);
                res[i]^=mex(a);
            }
        }
        for(int i=0;i<m;i++){
            if(res[i]) printf("W");
            else printf("L");
        }
        printf("\n");
    }
    return 0;
}

Nim or not Nim?取或 分成两堆

Description

Nim is a two-player mathematic game of strategy in which players take turns removing objects from distinct heaps. On each turn, a player must remove at least one object, and may remove any number of objects provided they all come from the same heap.

Nim is usually played as a misere game, in which the player to take the last object loses. Nim can also be played as a normal play game, which means that the person who makes the last move (i.e., who takes the last object) wins. This is called normal play because most games follow this convention, even though Nim usually does not.

Alice and Bob is tired of playing Nim under the standard rule, so they make a difference by also allowing the player to separate one of the heaps into two smaller ones. That is, each turn the player may either remove any number of objects from a heap or separate a heap into two smaller ones, and the one who takes the last object wins.

Input

Input contains multiple test cases. The first line is an integer 1 ≤ T ≤ 100, the number of test cases. Each case begins with an integer N, indicating the number of the heaps, the next line contains N integers $s[0],s[1],....,s[N-1]$, representing heaps with $s[0],s[1],...,s[N-1]$ objects respectively.$(1\le N\le 10^6,1\le S[i]\le 2^{31}-1)$

Output

For each test case, output a line which contains either “Alice” or “Bob”, which is the winner of this game. Alice will play first. You may asume they never make mistakes.

Sample Input
2
3
2 2 3
2
3 3

Sample Output
Alice
Bob

题意:Alice和Bob轮流取N堆石子，每堆S[i]个，Alice先，每一次可以从任意一堆中拿走任意个石子，也可以将一堆石子分为两个小堆。先拿完者获胜。
game那题是在某堆取若干石子后可以将该堆分成两堆
这题是，要么取走石子，要么将某堆分成两堆，显然要用到SG函数
根据SG函数基本思路，进行到定义f数组大小的时候就被卡住
可能出现的局面又石子个数决定，数据范围高达$2^{31}-1$,一来尽管在全局区能开的数组很大，但经测试，也不能到达int f[1e9],二来在枚举可能的后继局面时一定超时
由此，想到减小范围，打表找规律

注意： 一个局面拆分成了两个局面，由SG函数理论，
多个独立局面的SG值，等于这些局面SG值的异或和。

#include 
#include 
#include 
using namespace std;
//const int M=pow(2,31)-1; //这么大的数组，非常离谱 
const int M=1e8;
int f[M];//记忆化递归记录每种可能出现局面的SG值
//f数组该开多大呢，可能出现的局面有多少种呢
//显然石子数相同的堆的SG值相同，f数组范围和石子数量有关  

int SG(int x){
	if(f[x]!=-1)return f[x];
	set<int> S;
	for(int i=0;i<x;i++){
	//通过取走非零个石子或者分成两堆，石子为x的局面的后继局面，
//	包括石子数为小于x的所有非负数的这所有局面
//	eg. 2的后继局面有(0),(1),(1,1)
//	3的后继局面有(0)(1)(2)(1,2) 
//	4的后继局面有 (0)(1)(2)(3)(1,3)(2,2) 
		S.insert(SG(i));
	}
//	一个局面拆分成了两个局面，由SG函数理论，
//	多个独立局面的SG值，等于这些局面SG值的异或和。
	for(int i=1;i<x;i++){
		S.insert(SG(i)^SG(x-i));
	}
	for(int i=0;;i++){
		if(!S.count(i)){
		f[x]=i;
		return f[x];
		}
	}
	
} 
int main(){
	int t;
	cin>>t;
	int n;
	while(t--){
//		cin>>n;
//		int x;
//		int res=0;
		fill(f,f+M,-1);
//		for(int i=0;i
//			cin>>x;
//			res^=SG(x);
//		}
//		if(res)cout<<"Alice"<
//		else cout<<"Bob"<
		for(int i=1;i<150;i++){
			cout<<SG(i)<<" ";
			if(i%4==0)cout<<endl;
		}
	}
    return 0;
}

只是将4的倍数和它前一个数进行调换了

#include 
using namespace std;
int SG(int x){
	if(x%4==0)return x-1;
	if(x%4==3)return x+1;
	return x; 
} 
int main(){
	int t;
	cin>>t;
	int n;
	while(t--){
		cin>>n;
		int x;
		int res=0;
//		fill(f,f+M,-1);
		for(int i=0;i<n;i++){
			cin>>x;
			res^=SG(x);
		}
		if(res)cout<<"Alice"<<endl;
		else cout<<"Bob"<<endl;

	}
    return 0;
}

A New Stone Game

A New Stone Game
题意：给定几个堆的石子，A和B分别拿一个堆中任意数量的石子，然后可放可不放到其他有石子的堆中，谁最后没有石子拿谁就输了。每次都是A先拿，输出1代表A赢，输出0代表B赢
（取后可放可不放，是根据Description中给出的样例，题目中有freely，真心看不太出来)

game:取后可以选择分成两堆或者不分
Nim or not Nim：要么取，要么分两堆
A New Stone Game：取后不干或者把这堆中若干个移到别的不为0的堆（可以挪到不同的几堆（分配到其余若干堆）

从最小最简单的情况搞起

博弈论还有很多类型的题目，都是从最小的情况最简单的情况开始想，之后在往后面去推，当然dp这种就更不用说了
从最小最简单的情况搞起，再往后面推是一个好方法

分析：

一堆(a1)，先手必胜
两堆
(1,1)先手败
(2,2)先手取1挪1(0,3)/先手取2(0,2),先手败
(3,3)先手取1挪1(1,4),后手取1挪1(2,2),先手败
初可窥见规律，若两堆石子数相同，先手在一堆做何种操作，后者再另一堆
模仿先手做相同操作，可使两堆数目重归一致，即把两堆数量一致的局面
抛给先手，最后的(0,0)也将属于先手，先手必败
以上只是通过枚举了先手所有取后放到别堆的情况，都是必败
取后不放到别堆的情形更加简单，依旧是后手重复先手操作

两堆石子数相同是先手必败局面
两堆石子数不同是先手必胜局面
(1,2)先手采用最佳决策不会取第一堆，在第2堆取1个，把必败局面抛给对手
(1,3)相似
对于规模为2 的局面已经得出上述结论，试着套用在规模更大的局面中，
测试是否正确
首先易得，偶数堆，并且两两相等的情况，一定是先手必败
后手只需要重复或者说是进行对手的对称操作保持两两相等的局面
例如，1，3两堆相等 ，2，4两堆相等 ，先手在第1堆取完再向第4堆放，
后手就在第3堆取相同数再向2放相同数

接着考虑奇数堆
3堆
0堆相同(1,2,3),第3堆取2放一个到第1堆
2堆相同(2,2,3),取走3
3堆相同(2,2,2),取走一个2
发现只有3堆时，先手可以通过一次决策将石子变成相等的两堆
推广到更大范围，奇数堆，可以将最多的那堆消减掉变成偶数堆
怎么分配最多的那堆呢？按升序排列石子堆，相邻两堆为1组，
让最大的那堆去补足每一组的差距，使每一组中两堆都相等
多余的自然是一开始取走的（最佳决策嘛，先算出差距之和）
最多一堆的石子绝对是足够多，通过绘制各堆的条形图就可以窥见

若偶数堆，并非两两相等，
先手可以一次操作构成两两相等的局面，howtodo
只要将最多的堆削弱到和最少的堆相等，如何分配削弱的所有石子，
一部分取走，剩下的由于恰好补足剩余各组的差距，从而构成偶数对
两两相等堆的必败局面抛给对手

#include 
#include  
using namespace std;
const int N=20;
int h[N];
int main(){
	int n;
	while(cin>>n&&n){//先手必败：偶数堆且两两相等 
		for(int i=0;i<n;i++){
			cin>>h[i];
		}
		sort(h,h+n);
		bool f=true;//假设后手胜 
		if(n&1)f=false;
		else{
			for(int i=0;i<n;i+=2){
				if(h[i]!=h[i+1]){
					f=false;
					break;
				}
			}
		}
		if(f)cout<<"0"<<endl;
		else cout<<"1"<<endl; 
	} 

    return 0;
}

参考思路

Georgia and Bob

Georgia and Bob
题意：给定n个棋子和它们分别的初始位置，两位玩家的操作是：选择一枚棋子向左移动若干步，不能跨越别的棋子，也不能跨过左边界

思路一：阶梯Nim

阶梯Nim就是每一次把一级阶梯上的若干石子（非零）移到下一级台阶上，直到不能移动为止。
先手必胜的条件是奇数级上的石子数异或和非零。
相当于取出奇数层石子，做Nim游戏。因为偶数阶的石子落地都需要偶数次移动。
先手总有办法使奇数阶上的石子异或和为0的局面抛给对手，对手面临奇数阶上石子异或为0的局面，要么无法操作输了，要么操作，不管移动奇数阶还是偶数阶石子，某一奇数阶上的石子必将发生变化，从而使奇数阶上的石子异或和为0，必将必胜态抛回先手。
拟合阶梯Nim
试想将一枚棋子向前移动若干步，它与前一枚棋子之间的距离减小，与后一枚棋子之间的距离增大，前者减小的距离等于后者增大的距离，很容易想到阶梯Nim中将一级阶梯上的石子移到下一级阶梯
将这题与阶梯Nim拟合，当前n-1枚棋子与它们分别的前一颗棋子相隔距离都为0且第n枚棋子与它前一枚棋子之间的距离也为0（同时很容易想到，取石子游戏中石子数为0的状态相当于这里每两枚棋子之间的距离为0，显然，这里可以用两枚棋子之间的距离表示石子数量），此时为必败态，那么说明，我们要将 第n枚棋子与第n-1枚棋子之间的距离 看作第1级阶梯上的棋子（因为某枚棋子向左移，与前一枚棋子之间的距离减小，与后一枚棋子之间的距离增大，相当于是前面那堆移到后面那堆，与阶梯Nim中石子向下移拟合，最后面的那堆就是第一级上的石子。反证法也可说明，假设第1枚和第2枚之间的距离是第1级阶梯上的石子，其余阶梯上都没有石子，依旧不能说明是必胜态）

#include
#include
#include
using namespace std;
int t,n;
int a[1005];
int main(){
	cin>>t;
	while(t--){
		cin>>n;
		int ans=0;
		for(int i=1;i<=n;i++){
			cin>>a[i];
		}
		sort(a+1,a+n+1); 
		// for(int i=1;i<=n;i+=2)s^=a[n-i+1]-a[n-i]-1;
		for(int i=n;i>=1;i-=2){
			ans^=a[i]-a[i-1]-1;
		}
		if(ans)cout<<"Georgia will win"<<endl;
		else cout<<"Bob will win"<<endl;
	}
}

思路二：SG函数实现n-Nim

1棋 棋子挨着 不存在的第0个位置，先手败，棋子与不存在的第0个位置之间距离大于0，先手胜
2棋 两棋相邻先手败(先手只能移前一个棋，后手紧跟)
两栖不相邻，先手不会移第一个(后手会紧跟上来),而回采取最佳决策，将棋子2移到紧跟棋子一，先手胜
可以想到，每两枚棋子为一组，每组两枚棋子之间的距离都为0时为必败态。那么把每组棋子之间的距离看成一堆石子，这组之间的距离可想成是个状态有向图。
那么那么我们考虑两个棋子距离为0是从哪里转移而来的：两个棋子如果没有距离了，那么它肯定是从一开始有距离的游戏状态转移过来的.

那么我们可以得到一些式子：

sg(距离为1)=mex(sg(距离为0))=1,

sg(距离为2)=mex(sg(距离为0),sg(距离为1))=2,

sg(距离为3)=mex(sg(距离为0),sg(距离为1),sg(距离为2))=3…
SG值得到的非常轻易，显然，这是个变种的Nim游戏（一堆石子进行取走操作，那么原始局面对应的SG值就是石子数，因为可以取走若干，mex值0~（石子数-1）都出现过了

因此，我们把2个棋子看做1组，之间的空位数看做一堆石子，最后按照nim游戏计算即可
参考

思路三：普通取数Nim

两枚棋子之间的距离为0为必败态，分析这题的P/N点时，和往常不一样，不是从小数据推测，而是直接从性质推测，从右往左，把棋子分为两两一组，如果是奇数颗棋子，就补第一颗的位置为0，如果是偶数颗棋子，两两石子之间距离为0一定是必败态，因为先手只能移动前一颗石子，后手紧跟）。当对手移动两颗棋子的左边的棋子时，我们只需要把右边这颗棋子移动相同的步数就行，当对手移动右边的棋子时，把两颗棋子之间的距离看为石子的个数，我们只需按照取石子的规则走就行。

#include
#include
#include
#include
using namespace std;
int a[1010];
int main()
{
    int t,n;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        for(int i=0;i<n;i++)
        scanf("%d",&a[i]);
        int ans=0;
        sort(a,a+n);
        if(n&1)
        {
            ans^=(a[0]-1);
            for(int i=2;i<n;i+=2)
            ans^=(a[i]-a[i-1]-1);
        }
        else
        for(int i=1;i<n;i+=2)
        ans^=(a[i]-a[i-1]-1);
        //cout<
        if(ans!=0)
        puts("Georgia will win");
        else
        puts("Bob will win");
    }
}
/*
3
3
1 2 3
8
1 5 6 7 9 12 14 17
Bob will win
Georgia will win
*/

JZOJ4178【NOI2015模拟YDC】游戏（阶梯nim游戏）

Problem

Input

Output

Hint

jzoj 4024 石子游戏 {筛素数+博弈论（NIM博弈/SG函数）}

Problem
　　本题有T组测试数据。
　　给出N堆石子。A 和 B 轮流操作，A 先手。操作者在每一轮中必须选择一堆石子，并且作出下列两种操作中的一种：
　　（1）移走整堆石子
　　（2）设这堆石子中有 N 个，你可以从中取出 Y 个石子，若 Y 满足与N互质。
取走最后一个石子的人胜出。若 A 和 B 都以最优策略执行，对于每组数据，询问最后谁会胜利。

Hint
20%的数据，N<=5，每堆石子数量少于10
100%的数据，T<=100，N<=100，每堆石子数量不大于1,000,000

内存分区

#include 
const int N=1e6+5;
int a[N];//全局变量，编译运行，正常输出 
using namespace std;
int main(){
//	int b[N];
//局部变量，虽然编译未报错overflow，但空间到达e6数量级就无法输出 
	cout<<"年后"; 
    return 0;
}

在解释原因前我们先看一下一个由C/C++编译的程序占用的内存分为几个部分：

1、栈区(stack segment):由编译器自动分配释放，存放函数的参数的值，局部变量的值等。在Windows下，栈是向低地址扩展的数据结构，是一块连续的内存的区域。这句话的意思是栈顶的地址和栈的最大容量是系统预先规定好的，

在WINDOWS下，栈的大小是2M(也有的是1M，总之是一个编译时就确定的常数)，如果申请的空间超过栈的剩余空间时，将提示overflow。因此，能从栈获得的空间较小。

2、堆区(heap segment):一般由程序员分配释放，若程序员不释放，程序结束时可能由系统回收。它与数据结构中的堆是两回事。堆是向高地址扩展的数据结构，是不连续的内存区域。这是由于系统是用链表来存储的空闲内存地址的，自然是不连续的，而链表的遍历方向是由低地址向高地址。堆的大小受限于计算机系统中有效的虚拟内存。由此可见，堆获得的空间比较灵活，也比较大。
3、全局区（静态区）(data segment):全局变量和静态变量的存储区域是在一起的，程序结束后由系统释放。数据区的大小由系统限定，一般很大。
全局变量会自动初始化（全局变量和静态变量的存储是放在一块的，初始化的全局变量和静态变量在一块区域， 未初始化的全局变量和未初始化的静态变量在相邻的另一块区域）
4、文字常量区：常量字符串就是放在这里的，程序结束后由系统释放。
5、程序代码区：存放函数体的二进制代码。

综上所述，局部变量空间是很小的，我们开一个a[1000000]就会导致栈溢出；而全局变量空间在Win32bit下可以达到4GB，因此不会溢出。

待学

SJ定理？
巴什博弈（Bash Game）、威佐夫博奕（Wythoff Game）、尼姆博奕（Nim Game）
博弈论的算法总结
博弈基础知识总结
博弈类题目小结（HDU,POJ,ZOJ）
尼姆博奕（Nimm Game）
博弈论题目集 （持续更新）

参考

y总讲解 之 Acwing常用代码模板4——数学知识
OI-Viki公平组合游戏
好文，我去